虽然名字里带回归,但实际上是一种分类方法,主要用于两分类问题,即只有两种分类
优点:计算代价不高,易于理解和实现
缺点:容易欠拟合,分类精度可能不高
线性回归函数
??\(\small z = f(X) = XW\)
??其中
????X 是特征值
????W 是回归系数
??X 和 W 都是向量,可展开为
????\(\small z = XW = X_{0}W_{0} + X_{1}W_{1} + ... + X_{n}W_{n}\)
??线性方程其实应该是
????\(\small z = XW + b\)
??为此这里固定
????\(\small X_{0}=1\)
????\(\small W_{0}=b\)
??其他 X 值才是用户输入,这样变成两个向量相乘方便计算
逻辑回归函数 (Sigmoid 函数)
??\(\small y=g(z)=\frac{1}{1+e^{-z}}\)
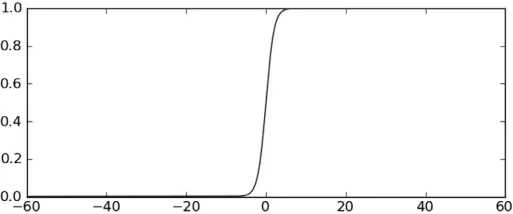
??该函数模拟阶跃函数 (在某个跳跃点从 0 瞬间跳到 1,跳跃点两边的值固定为 0 和 1)
??可以得出
????\(\small y=\left\{\begin{matrix}0.12&z=-2\\0.5&z=0\\0.88&z=2\end{matrix}\right.\)
??且满足
????\(\small g(z) + g(-z) = 1\)
??
??在 z 轴比较长的情况下看起来就像跳跃点为 0 的阶跃函数
??
分类器
??结合线性回归函数和逻辑回归函数
????\(\small y=g(z)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-XW}}\)
??
??对特征向量 X 进行计算,得出 0~1 之间的值
??大于 0.5 属于分类 1,小于 0.5 属于分类 0
??所以逻辑回归也可以被看成是一种概率估计
训练分类器
??通过最优化算法(通常是梯度下降算法),寻找最佳回归系数 W 的值
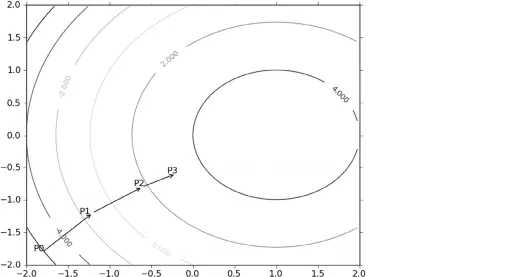
要找到某函数的最小值,最好的方法是沿着该函数的梯度方向向下探寻
就像等高线,选择最高点的最快方法就是不断沿着梯度走
逻辑回归函数 \(\small g(z)\) 的结果实际是一个 \(\small (0,1)\) 区间的概率估计
为此损失函数采取逻辑损失函数
??\(\small L = -(y)log(g(z)) - (1-y)log(1-g(z))\)
当 \(\small y = 0\) 时,\(\small L = -log(1-g(z))\),\(\small g(z)\)范围是\(\small (0,1)\),对应 L 范围是 \(\small (0,\infty)\)
当 \(\small y = 1\) 时,\(\small L = -log(g(z))\),\(\small g(z)\)范围是\(\small (0, 1)\),对应 L 范围是 \(\small (\infty, 0)\)
梯度下降算法的目的就是找最佳的 \(\small w\) 参数,使得所有样本的 \(\small L\) 值的总和最小
??\(\small L(w) = - \sum_{i=0}^{n}(\ (y)log(g(z)) + (1-y)log(1-g(z))\ )\)
梯度算法的迭代公式如下
??\(\small w := w - \alpha\nabla L(w)\)
其中
??\(\small \nabla L(w)\) 是函数 \(\small L\) 在 \(\small w\) 处的梯度,代表使 \(\small L\) 值变化率最大的方向
??\(\alpha\) 是步长,即沿梯度方向变化的大小,必须取一个很小的值
该公式一直被迭代执行,即\(\small w\) 沿着梯度方向不断减少,使\(\small L\)值以最快的速率不断下降
直至达到某个停止条件,如迭代次数达到阈值,或\(\small L\)值达到某个可以允许的误差范围
进一步了解梯度,参考 导数、偏导数、方向导数、梯度、梯度下降
??
??
已知对下列函数求导
??\(\small g(z) = \frac{1}{1+e^{-z}}\)
??\(\small f(x) = log(x)\)
可得
??\(\small \frac{\partial g(z)}{\partial z}=g(z)(1-g(z))\)
??\(\small \frac{\partial f(x)}{\partial x}=\frac{1}{x}\)
梯度在每个轴上的分量是函数在该轴的偏导数
??\(\small \nabla L(w) = (\frac{\partial L(w)}{\partial w_{0}}, ... , \frac{\partial L(w)}{\partial w_{i}}, ... , \frac{\partial L(w)}{\partial w_{m}})\)
结合以上内容求解 \(\small L(w)\) 的偏导数(i 代表样本,共 n 个,j 代表特征,共 m 个)
?
? ?\(\small \frac{\partial L(w)}{\partial w_{j}}=-\sum_{i=0}^{n}(\frac{\partial((y)log(g(z)))}{\partial w_{j}}+\frac{\partial((1-y)log(1-g(z)))}{\partial w_{j}})\)
??????\(\small = -\sum_{i=0}^{n}(y\frac{1}{g(z)}\frac{\partial g(z)}{\partial w_{j}}-(1-y)\frac{1}{1-g(z)}\frac{\partial g(z)}{\partial w_{j}})\)
??????\(\small = -\sum_{i=0}^{n}((\frac{y}{g(z)}-\frac{(1-y)}{1-g(z)})\frac{\partial g(z)}{\partial w_{j}})\)
??????\(\small = -\sum_{i=0}^{n}((\frac{y}{g(z)}-\frac{(1-y)}{1-g(z)})g(z)(1-g(z))\frac{\partial z}{\partial w_{j}})\)
??????\(\small = -\sum_{i=0}^{n}((y(1-g(z))-(1-y)g(z))\frac{\partial xw}{\partial w_{j}})\)
??????\(\small = -\sum_{i=0}^{n}((y-g(z))\frac{\partial xw}{\partial w_{j} })\)
??????\(\small = -\sum_{i=0}^{n}((y-g(z))x_{j})\)
??????\(\small = -\sum_{i=0}^{n}(e^{(i)}x_{j}^{(i)})\)
??????\(\small = -\begin{bmatrix}x_{j}^{(0)}&...&x_{j}^{(i)}&...&x_{j}^{(n)}\end{bmatrix}\begin{bmatrix}e^{0}\\...\\e^{i}\\...\\e^{n} \end{bmatrix}\)
?
将所有偏导组成梯度
?
? ?\(\small \nabla L(w) = (\frac{\partial L(w)}{\partial w_{0}}, ... , \frac{\partial L(w)}{\partial w_{i}}, ... , \frac{\partial L(w)}{\partial w_{m}})\)
??????\(\small = -\begin{bmatrix}x_{0}^{(0)}&...&x_{0}^{(i)}&...&x_{0}^{(n)}\\x_{j}^{(0)}&...&x_{j}^{(i)}&...&x_{j}^{(n)}\\x_{m}^{(0)}&...&x_{m}^{(i)}&...&x_{m}^{(n)}\end{bmatrix}\begin{bmatrix}e^{0}\\...\\e^{i}\\...\\e^{n} \end{bmatrix}\)
??????\(\small = -X^{T}E\)
?
进一步求得梯度下降公式
?
??\(\small W = W - \alpha\nabla L(W)\)
?? ? \(\small = W + \alpha X^{T}E\)
? ?? \(\small = W + \alpha X^{T}(Y-g(XW))\)
?
其中
??样本集有 n 条数据,m 个特征
??X 是 \(\small (n,m)\) 矩阵
??W 是 \(\small (m,1)\) 矩阵
??Y 是 \(\small (n,1)\) 矩阵
??\(\small \alpha > 0\)
可以看到,每一次迭代都要对所有样本计算,计算量太大
可以改为每一次迭代都随机取一部分样本计算就可以
# coding=utf-8
import numpy as np
import random
# 阶跃函数
def sigmoid(z):
return 1.0/(1+np.exp(-z))
# 梯度下降算法
# 根据样本(X,Y) 算法最佳的 W
def gradDescent(sampleData, classLabels):
"""
sampleData - 样本特征,(n,m) 的二维数组,n 是样本数,m 是特征数
每行的第一个值 X0 固定为 1,从 X1 开始才是真正的特征值,目的是简化向量的计算
y = x1*w1 + ... + xm*wm + b
= x1*w1 + ... + xm*wm + x0w0
= XW
classLabels - 样本标签,(1,n) 的一维数组
"""
# 转为 NumPy 矩阵
dataMatrix = np.mat(sampleData)
# 将 (1,n) 转为 (n,1) 方便后面的矩阵计算
labelMatrix = np.mat(classLabels).transpose()
# n 个样本,m 个特征值
n, m = np.shape(dataMatrix)
# 梯度下降的步长
alpha = 0.001
# 最大迭代次数
maxCycles = 500
# 初始化 W 为 (m,1) 数组, 默认值为 1
weights = np.ones((m, 1))
# 迭代
for k in range(maxCycles):
# (n,m) 矩阵乘以 (m,1) 矩阵,得到 (n,1) 矩阵,再通过逻辑回归函数得到样本的 Y
h = sigmoid(dataMatrix*weights)
# 两个 (n,1) 矩阵,得到每个样本的误差
error = (labelMatrix - h)
# w = w + a*(X^T)*(Y-g(XW))
# = w + a*(X^T)*E
weights = weights + alpha * dataMatrix.transpose() * error
return weights
# 分类
def classify(data, weights):
dataMatrix = np.mat(data)
resultMatrix = sigmoid(dataMatrix * weights) > 0.5
"""
for result in resultMatrix:
print(result.item())
"""
return resultMatrix
# 随机梯度
def stocGradDescent0(sampleData, classLabels):
dataMatrix = np.mat(sampleData)
labelMatrix = np.mat(classLabels).transpose()
n, m = np.shape(dataMatrix)
alpha = 0.01
weights = np.ones((m, 1))
for i in range(n):
# 每次迭代只取一个样本,迭代次数为样本个数
h = sigmoid(dataMatrix[i]*weights)
error = labelMatrix[i] - h
weights = weights + alpha * dataMatrix[i].transpose() * error
return weights
# 改进的随机梯度
def stocGradDescent1(sampleData, classLabels, numIter=150):
dataMatrix = np.mat(sampleData)
labelMatrix = np.mat(classLabels).transpose()
n, m = np.shape(dataMatrix)
weights = np.ones((m, 1))
# 自己选择迭代次数
for j in range(numIter):
dataIndex = range(n)
# 每次迭代又迭代了每一个样本
for i in range(n):
# 每次迭代都改变步长,0.0001 用于防止出现 0 的情况
alpha = 4/(1.0+j+i)+0.0001
# 随机选择一个样本
randIndex = int(random.uniform(0, len(dataIndex)))
h = sigmoid(dataMatrix[randIndex]*weights)
error = labelMatrix[randIndex] - h
# 计算新的 W
weights = weights + alpha * dataMatrix[randIndex].transpose() * error
# 删除该样本下标
del(dataIndex[randIndex])
return weights
原文:https://www.cnblogs.com/moonlight-lin/p/12329468.html