搜索（dfs）

必须要说，搜索不是简简单单看一篇博客就能明白的，需要经验累计才能理解。

所以我先简单说一下：

搜索分为dfs（深度优先搜索）和bfs（广度优先搜索）两种，而这两种方式可以说差别比较大，所以要分开说。

dfs（深搜）：

dfs是基于递归的一种搜索，所以它的实现是自己调用自己，一步一步向深处搜索，当出现死路时就“退一步”（专业来讲叫回溯），直到出现一条活路，然后

就沿着这条路一直搜下，直到出现死路再回溯。如此循环往复，直到嵌套的递归条件生效并停止这次深搜。堪称“不撞南墙不回头”啊。

这是一个比较直观的搜索流程

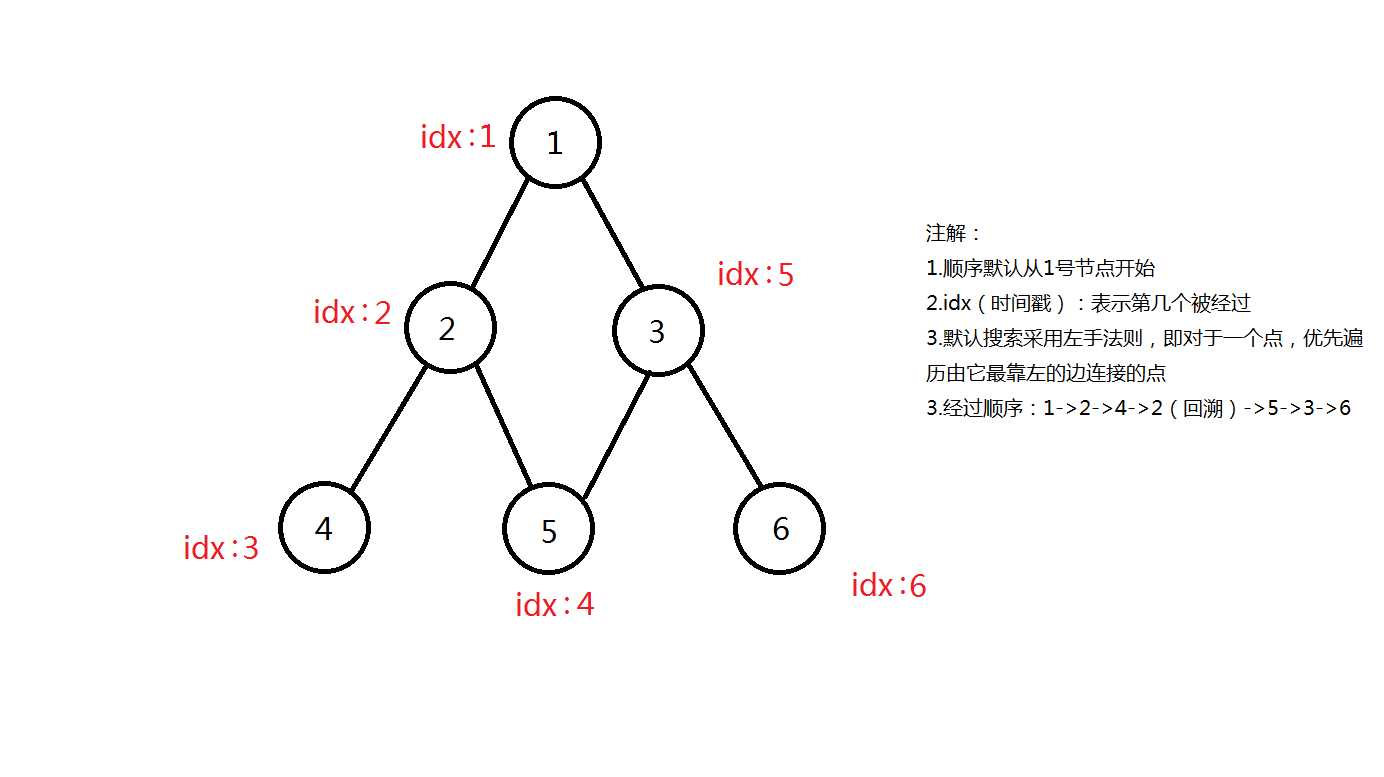
以上就是dfs对一张图的遍历了

现在讲完dfs算法了，接下来可以练几道dfs好题

https://www.luogu.com.cn/problem/P1706 全排列问题

详解：用一个dfs递归函数来枚举，在这道题中，图的深度就是该全排列确定到第几位，每次往“深”dfs就是确定完第x位后枚举第x+1位的数字可以取几，唯

一有所不同的是这道题还要开一个bool数组，记录到目前为止，数i是否被用过，以便枚举

其中idx表示枚举到了第idx位，ans用于记录答案，flag判断这个数是否被用过，而dfs(idx+1)后面那两句ans[i]=0,flag[i]=0是用于回溯，如果第idx为并没有取

数i，则flag与ans都要改变。

void dfs(int idx)//dfs枚举 
{
    if(idx>n)//如果把所有数都用上了，即已经生成一个全排列了 
    {
        for(int i=1;i<=n;i++)
        {
            printf("%5d",ans[i]);
        }
        cout<<endl;
        //生成成功后直接输出 
        return;
        //return必不可少，否则不断枚举下去，会死循环 
    }
    for(int i=1;i<=n;i++)
    {
        if(flag[i]) continue;//如果该数字被用过，直接跳过即可
        flag[i]=1;//标记这个数已经被用过 
        ans[idx]=i;//记录答案 
        dfs(idx+1);//往深枚举 
        flag[i]=0;
        ans[idx]=0;//回溯 
    }
}

这是一道最简单的dfs了，简直是模板级的。

当然，还有别的较难的题

如https://loj.ac/problem/10018数的划分等等

https://loj.ac/problems/search?keyword=1.3

这里面除了A+B problem以外都是比较有意思的深搜题，建议大家多去刷一刷，十分有助于提高水平！

搜索（dfs）

原文：https://www.cnblogs.com/chen-1/p/12328832.html