字典树,又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。(引自百度百科《字典树》)
NKOJ 1934 外地人
你考入大城市沙坪坝的学校, 但是沙坪坝的当地人说着一种很难懂的方言, 你完全
听不懂。 幸好你手中有本字典可以帮你。 现在你有若干个听不懂的方言需要查询字典。
输入格式:
第一行,两个整数n和m。
接下来有n行表示字典的内容,每行表示一条字典的记录。每条记录包含两个空格间隔的单词,第一个单词为英文单词,第二个单词为对应的沙坪坝方言。
接下来有m行,每行一个单词,表示你要查询的沙坪坝方言。
输出格式:
输出m行,每行一个英文单词,表示翻译后的结果。
如果某个单词字典查不到,输出"eh"
样例输入:
5 3
dog ogday
cat atcay
pig igpay
froot ootfray
loops oopslay
atcay
ittenkay
oopslay
样例输出:
cat
eh
loops
注:所有单词都用小写字母表示, 且长度不超过10。
传送门:http://oi.nks.edu.cn/zh/Problem/Details/1934
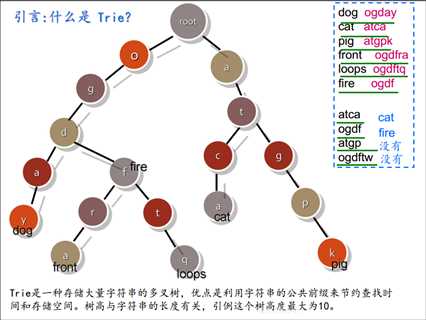
1. 根节点不包含字符, 除根节点外每一个节点都只包含一个字符。
2. 从根节点到某一节点, 路径上经过的字符连接起来, 为该节点对应的字符串。
3. 在trie树中查找一个关键字的时间和树中包含的结点数无关, 而取决于组成关键字的字符数。 也就是查找字符串s的时间为O(s.length())
4. 如果要查找的关键字可以分解成字符序列且不是很长, 利用Trie树查找速度优于二叉查找树。
如:若关键字长度最大是5, 则利用Trie树, 利用5次比较可以从265=11881376个可能的关键字中检索出指定的关键字。 而利用二叉查找树至少要进行log2265=23.5次比较。
接下来先给出引例题解的main函数部分(部分初始化未给出)——
struct node { int Num; //如果该节点是一个单词的结尾,记录对应单词的编号 int Next[26]; //儿子节点的编号 }trie[1000001]; string s[100001], a; int main() { cin >> n >> m; for (k = 1; k <= n; k ++){ cin >> s[k] >> a; Insert(a, k); } for (k = 1; k <= m; k ++) { cin >> a; ans = Find(a); if (ans)cout << s[ans]; else cout << "eh" << endl; } return 0; }接着是两个函数的部分——
void Insert(string c, int k) { int i, t, len, p = 1; len = c.length(); for (i = 0; i < len; i ++) { t = c[i] - ‘a‘;//将字符c[i]转换成值为0到25的数字,比如‘a‘转换为0,‘b‘转换为1,‘c’转换为2…… if (trie[p].Next[t] == 0) { //若p没有值为t的儿子 tot ++; //新增一个编号为tot的节点 trie[p].Next[t] = tot; //记下p的值为t的孩子节点的编号 p = trie[p].Next[t]; //p指向新添加的节点 trie[p].Num = 0; //初始化新添加的节点,将其标记为不是单词的结尾 } else p = trie[p].Next[t]; //若p存在值为t的儿子,p指向该儿子,继续讨论 } trie[p].Num = k; //for循环已执行完,说明第k个单词已加入,在单词结尾做上标记 }
int Find(string c) { int i, t, len, p = 1; len = c.length(); for (i = 0; i < len; i ++) { t = c[i] - ‘a‘; if (trie[p].Next[t] == 0)return 0; //当前要匹配值为t的字母,若没有则结束 p = trie[p].Next[t]; //若存在值为t的字母,则继续匹配 } return trie[p].Num; //若for循环执行完毕,说明找到了需要的单词,返回其编号 }以上的代码几乎就是字典树的模板,在不同的题中main函数或许有所不同,可以借此熟悉一下字典树的工作原理,再酌情修改。
trie树简单题:
#include<bits/stdc++.h>
using namespace std;
int tot,n,m;
string s;
struct node{
int num,nxt[30];
}trie[1000005];
map<string,int>mp,mpp;
int Insert(string ss,int k){
int p=1,len=ss.length();
for(int i=0;i<len;i++){
int t=ss[i]-‘a‘;
if(trie[p].nxt[t]==0){
tot++;
p=trie[p].nxt[t]=tot;
trie[p].num=0;
}
else p=trie[p].nxt[t];
}
trie[p].num=k;
}
int myfind(string ss)
{
int len=ss.length();
int p=1;
for(int i=0;i<len;i++){
int t=ss[i]-‘a‘;
if(trie[p].nxt[t]==0) return 0;
p=trie[p].nxt[t];
}
return 1;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++){
cin>>s;
Insert(s,i);
}
cin>>m;
for(int i=1;i<=m;i++){
cin>>s;
if(myfind(s)==0) cout<<"WRONG"<<endl;
else if(myfind(s)&&mpp[s]==0) {cout<<"OK"<<endl;mpp[s]++;}
else cout<<"REPEAT"<<endl;
}
}
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int maxn=100005,maxnode=200005;
int n;
bool ok;
struct node {
int num,next[10];
};
struct Trie{
int size;
string s[maxn];
node trie[maxn];
void set (){
size=1;
memset(trie,0,sizeof(trie));
}
int idx(char x){ return (int) x-‘0‘;}
bool insert(string a,int id){
int i,p=1,t,len=a.length();
bool sub=true; //是否新建了节点
for(i=0;i<len;i++)
if(isdigit(a[i])){
if(trie[p].num) return true; ///走到了别的单词结尾 ,相对于模板其实主要就是多了这里的判断
t=idx(a[i]);
if(!trie[p].next[t]){
sub=false; ///如果新建了节点说明并没有完整地遍历出树上字符串的的前缀
p = trie[p].next[t]= ++size;
trie[p].num=0;
}
else p=trie[p].next[t];
}
trie[p].num=id;
return sub;
}
} solver;
int main(){
ios_base::sync_with_stdio(false);
int t,i;
string num;
cin>>t;
while(t--){
solver.set(); //初始化
cin>>n;
ok=false;
for(i=1;i<=n;i++){
cin>>num;
if(!ok&&solver.insert(num,i)){ //出现了前缀
cout<<"NO"<<endl;
ok=true;
}
}
if(!ok)cout<<"YES"<<endl;
}
}
这道题其实就是相对于模板多出了一个步骤,就是每次将你要查询的字符串查到没有了以后,再把这个字符串没有的地方重新开始遍历查找
#include<bits/stdc++.h>
using namespace std;
long long n,m,sum;
string a;
int mark[1000005];
struct node
{
int son[26];
int mark;
}trie[1000005];
void add(string s)//建树
{
long long pos=0;
for(long long i=0;i<=s.size()-1;i++)
{
int now=s[i]-‘a‘;
if(trie[pos].son[now]==0) trie[pos].son[now]=++sum;
pos=trie[pos].son[now];
}
trie[pos].mark=1;//单词结尾标记
}
void find(string s)
{
int ans,pos=0;
memset(mark,0,sizeof(mark));//每找一个字符串都要初始化!
for(int j=0;j<=s.size()-1;j++) //先跑一遍!不然下面的循环直接一路continue过去了qwq
{
int now=s[j]-‘a‘;
pos=trie[pos].son[now];
if(pos==0) break;
if(trie[pos].mark==1) mark[j]=1;
}
for(int i=0,k;i<=s.size()-1;i++)
{
if(!mark[i])continue; else ans=i+1;
pos=0;
for(int j=i+1;j<=s.size()-1;j++)
{
int now=s[j]-‘a‘;
pos=trie[pos].son[now];
if(pos==0) break;
if(trie[pos].mark==1) mark[j]=1;
}
}
printf("%d\n",ans);
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a;
add(a);
}
for(int i=1;i<=m;i++)
{
cin>>a;
find(a);//查找
}
return 0;
}
思路:
Trie 树+搜索
我用的是dfsdfs
首先对于将所有的RNA片段都建到TrieTrie树里去,之后来匹配那个模板串就好了
如果是匹配的位置是字母,那么我们就继续往下匹配
如果是??,我们必须要略过TrieTrie树上的一位去匹配
如果是*∗,我们可以先考虑直接忽略这一位,也可以直接把这一位当成??来看,或者是在TrieTrie树上略过一位,但是在模板串上的匹配仍为当前位置,这样就能实现在TrieTrie树上忽略多位进行匹配了
一旦某一位匹配成功了,我们如果还有状态到达这一步就没有什么必要了,所以开一个bitsetbitset来进行记忆化就好了
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#include<bitset>
#define re register
#define maxn 500005
int son[maxn][4],flag[maxn];
int n,m,cnt,L,ans;
char S[1001],T[1001];
std::bitset<1001> f[maxn];
inline int read()
{
char c=getchar();
int x=0;
while(c<‘0‘||c>‘9‘) c=getchar();
while(c>=‘0‘&&c<=‘9‘)
x=(x<<3)+(x<<1)+c-48,c=getchar();
return x;
}
inline int ch(char p)
{
if(p==‘A‘) return 0;
if(p==‘G‘) return 1;
if(p==‘T‘) return 2;
if(p==‘C‘) return 3;
}
inline void ins()
{
int len=strlen(S+1);
int now=0;
for(re int i=1;i<=len;i++)
{
if(!son[now][ch(S[i])]) son[now][ch(S[i])]=++cnt;
now=son[now][ch(S[i])];
}
flag[now]++;
}
void dfs(int now,int t)
{
if(t==L+1)//匹配成功
{
ans+=flag[now];
flag[now]=0;
return;
}
if(f[now][t]) return;
f[now][t]=1;//记忆化,因为?和*可以变成任意的字符,所以肯定会有重复的方案,故记忆化排除重复的方案还一直dfs浪费时间
if(T[t]>=‘A‘&&T[t]<=‘Z‘)
{
if(!son[now][ch(T[t])]) return;
dfs(son[now][ch(T[t])],t+1);
}//是字母,那么我们就继续往下匹配
else
{
if(T[t]==‘?‘)
{
for(re int i=0;i<4;i++)
if(son[now][i]) dfs(son[now][i],t+1);//在Trie上忽略一位,同时模板串匹配位置加1
}
if(T[t]==‘*‘)
{
dfs(now,t+1);//忽略*,即用0个字符来代替它
for(re int i=0;i<4;i++)
if(son[now][i]) dfs(son[now][i],t+1),dfs(son[now][i],t);
//第一个dfs直接把这一位当成$?$来看,第二个dfs就能实现一个*代替多个字符
}
}
}
int main()
{
scanf("%s",T+1);
L=strlen(T+1);
n=read();
for(re int i=1;i<=n;i++)
scanf("%s",S+1),ins();
dfs(0,1);
printf("%d\n",n-ans);
return 0;
}
原文:https://www.cnblogs.com/hgangang/p/12333970.html