1、矩阵的迹：
定义：
线性代数中，n乘n方阵A的迹，是指A的主对角线各元素的总和(从左上方至右下方的对角线)，比如：
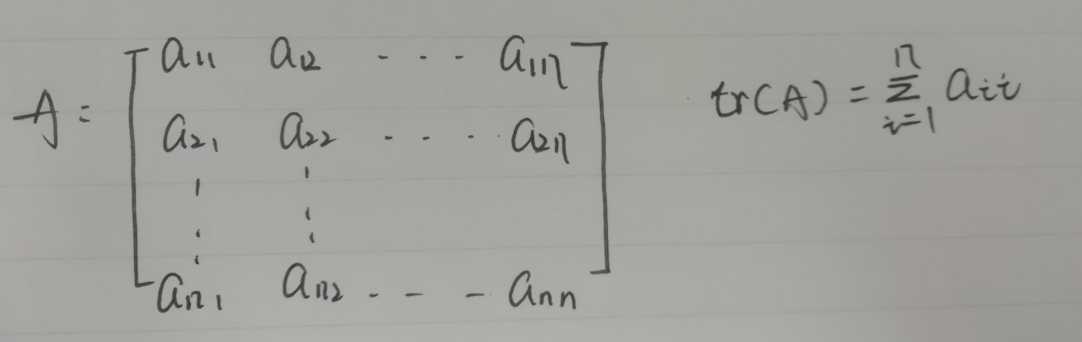
性质以及证明：
1、矩阵的迹等于特征值的和
特征值和特征向量
定义：
线性代数中，对于一个给定的矩阵
A，它的特征向量x，经过这个线性变换之后，得到的新向量
仍然与原来的
x保持在同一条直线上，但其长度或方向也许会改变。即
，其中
为标量，即特征向量的长度在该线性变换下缩放的比例，称
为其特征值。如果特征值为正，则表示在经过线性变换的作用后方向也不变；如果特征值为负，说明方向会反转；如果特征值为0，则是表示缩回零点。
求解：
得到
以后：
带入：
找出非0解就是特征向量了。
计算示例：
2、
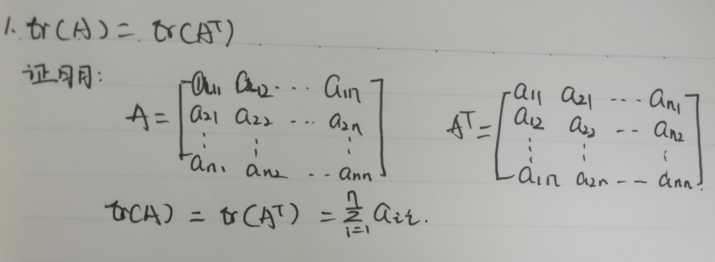
3、
4、
5、
原文：https://www.cnblogs.com/wjjcjj/p/12335670.html