动态规划（实战篇之数塔）

在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的： 

有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

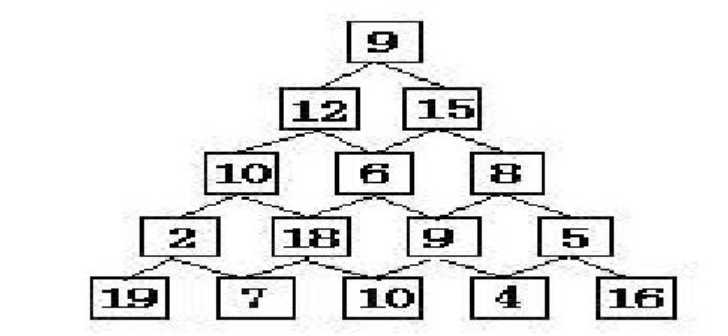
 Input输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度，接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内。 
Output对于每个测试实例，输出可能得到的最大和，每个实例的输出占一行。 
Sample Input

1
5
7
3 8
8 1 0 
2 7 4 4
4 5 2 6 5

Sample Output

30

 这种问题我们通常想到的是贪心法，据图分析：9 -> 15 -> 8 -> 9 -> 10    sum = 51

可是样例给的答案却是59。

问题出在哪里呢？？？

根据贪心法我们每次都会选择权值最大的路径行走，但是我们不能确保总和 sum 是最大的。

因此自上而下找最大值不太可行，不妨我们自下而上观察一下这张图：三角数字塔，越往顶上走路径越少。

正好应照了动态规划的思想：不断缩小区域直到找出正解。

我觉得我似乎解释得还是有点抽象，在此借鉴一下某大神对DP的看法：

http://blog.sina.com.cn/s/blog_169a33d090102y36t.html

再来看问题：从第 n - 1层看要想得到该层每个元素所经结点的最大值，要看max( A[i + 1][j]  , A[i + 1][j + 1] ),

　　　　　　以此类推：dp[i][j] =  max( dp[i + 1][j]  , dp[i + 1][j + 1] ) + A[i][j];

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <string>
using namespace std;
int main(){
    long long C;
    cin >> C;
    while(C--){
        int N;
        cin >> N;
        int dp[102][102];
        for(int i = 1; i <= N; i++){
            for(int j = 1; j <= i; j++){
                cin >> dp[i][j];
            }
        }

        for(int i = N - 1; i >= 1; i--){
            for(int j = 1; j <= i; j++){
                dp[i][j] += max(dp[i + 1][j], dp[i + 1][j + 1]);
            }
        }
        cout << dp[1][1] << endl;
    }

    return 0;
}

accept 

快夸我！！嘻嘻~

动态规划（实战篇之数塔）

原文：https://www.cnblogs.com/nibaba131237/p/12336527.html