本文学习笔记参照来源:https://tf.wiki/zh/basic/basic.html
学习笔记类似提纲,具体细节参照上文链接
一些前置的基础
随机数 tf.random uniform(shape())
两个元素零向量 tf.zeros(shape=(2))
2x2常量 tf.constant([1,2],[3,4])
查看形状、类型、值 A.shape A.dtype A.numpy()
矩阵相加 tf.add(A,B)
矩阵相乘 tf.matmul(A,B)
自动求导机制 tf.GradientTape()

import tensorflow as tf x = tf.Variable(initial_value=3.) with tf.GradientTape() as tape: # 在 tf.GradientTape() 的上下文内,所有计算步骤都会被记录以用于求导 y = tf.square(x) y_grad = tape.gradient(y, x) # 计算y关于x的导数 print([y, y_grad])

X = tf.constant([[1., 2.], [3., 4.]]) y = tf.constant([[1.], [2.]]) w = tf.Variable(initial_value=[[1.], [2.]]) b = tf.Variable(initial_value=1.) with tf.GradientTape() as tape: L = 0.5 * tf.reduce_sum(tf.square(tf.matmul(X, w) + b - y)) w_grad, b_grad = tape.gradient(L, [w, b]) # 计算L(w, b)关于w, b的偏导数 print([L.numpy(), w_grad.numpy(), b_grad.numpy()])
事例:线性回归(梯度下降)

import numpy as np X_raw = np.array([2013, 2014, 2015, 2016, 2017], dtype=np.float32) y_raw = np.array([12000, 14000, 15000, 16500, 17500], dtype=np.float32) X = (X_raw - X_raw.min()) / (X_raw.max() - X_raw.min()) y = (y_raw - y_raw.min()) / (y_raw.max() - y_raw.min())

对于多元函数 f(x) 求局部极小值,梯度下降 的过程如下: 初始化自变量为 x_0 , k=0 迭代进行下列步骤直到满足收敛条件: 求函数 f(x) 关于自变量的梯度 \nabla f(x_k) 更新自变量: x_{k+1} = x_{k} - \gamma \nabla f(x_k) 。这里 \gamma 是学习率(也就是梯度下降一次迈出的 “步子” 大小) k \leftarrow k+1 接下来,我们考虑如何使用程序来实现梯度下降方法,求得线性回归的解 \min_{a, b} L(a, b) = \sum_{i=1}^n(ax_i + b - y_i)^2 。

a, b = 0, 0 num_epoch = 10000 learning_rate = 1e-3 for e in range(num_epoch): # 手动计算损失函数关于自变量(模型参数)的梯度 y_pred = a * X + b grad_a, grad_b = (y_pred - y).dot(X), (y_pred - y).sum() # 更新参数 a, b = a - learning_rate * grad_a, b - learning_rate * grad_b print(a, b) # np.dot() 是求内积, np.sum() 是求和 # 手工求损失函数关于参数 a 和 b 的偏导数

#使用 tape.gradient(ys, xs) 自动计算梯度; #使用 optimizer.apply_gradients(grads_and_vars) 自动更新模型参数。 X = tf.constant(X) y = tf.constant(y) a = tf.Variable(initial_value=0.) b = tf.Variable(initial_value=0.) variables = [a, b] num_epoch = 10000 optimizer = tf.keras.optimizers.SGD(learning_rate=1e-3) for e in range(num_epoch): # 使用tf.GradientTape()记录损失函数的梯度信息 with tf.GradientTape() as tape: y_pred = a * X + b loss = 0.5 * tf.reduce_sum(tf.square(y_pred - y)) # TensorFlow自动计算损失函数关于自变量(模型参数)的梯度 grads = tape.gradient(loss, variables) # TensorFlow自动根据梯度更新参数 optimizer.apply_gradients(grads_and_vars=zip(grads, variables)) print(a, b)
模型的构建: tf.keras.Model 和 tf.keras.layers
模型的损失函数: tf.keras.losses
模型的优化器: tf.keras.optimizer
模型的评估: tf.keras.metrics
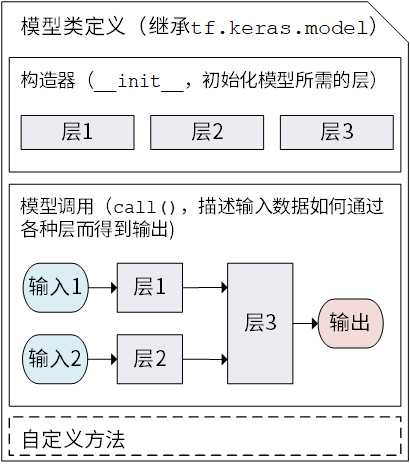
Keras 模型以类的形式呈现
通过继承 tf.keras.Model 这个 Python 类来定义自己的模型。
需要重写 __init__() (构造函数,初始化)和 call(input)(模型调用)两个方法
同时也可以根据需要增加自定义的方法。

class MyModel(tf.keras.Model): def __init__(self): super().__init__() # Python 2 下使用 super(MyModel, self).__init__() # 此处添加初始化代码(包含 call 方法中会用到的层),例如 # layer1 = tf.keras.layers.BuiltInLayer(...) # layer2 = MyCustomLayer(...) def call(self, input): # 此处添加模型调用的代码(处理输入并返回输出),例如 # x = layer1(input) # output = layer2(x) return output # 还可以添加自定义的方法

import tensorflow as tf X = tf.constant([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]]) y = tf.constant([[10.0], [20.0]]) class Linear(tf.keras.Model): def __init__(self): super().__init__() self.dense = tf.keras.layers.Dense( units=1, activation=None, kernel_initializer=tf.zeros_initializer(), bias_initializer=tf.zeros_initializer() ) def call(self, input): output = self.dense(input) return output # 以下代码结构与前节类似 model = Linear() optimizer = tf.keras.optimizers.SGD(learning_rate=0.01) for i in range(100): with tf.GradientTape() as tape: y_pred = model(X) # 调用模型 y_pred = model(X) 而不是显式写出 y_pred = a * X + b loss = tf.reduce_mean(tf.square(y_pred - y)) grads = tape.gradient(loss, model.variables) # 使用 model.variables 这一属性直接获得模型中的所有变量 optimizer.apply_gradients(grads_and_vars=zip(grads, model.variables)) print(model.variables)
全连接层 是 Keras 中最基础和常用的层之一
对输入矩阵 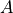 进行
进行 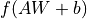 的线性变换 + 激活函数操作。
的线性变换 + 激活函数操作。
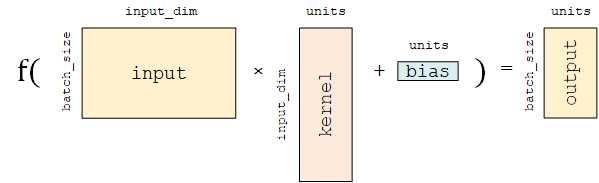
这里的等号其实是经过了一个激活函数后得到最后的结果
主要参数如下:
units :输出张量的维度;
activation :激活函数,对应于 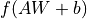 中的
中的 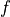 ,默认为无激活函数(
,默认为无激活函数( a(x) = x )。常用的激活函数包括 tf.nn.relu 、 tf.nn.tanh 和 tf.nn.sigmoid;
use_bias :是否加入偏置向量 bias ,即 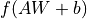 中的
中的 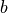 。默认为
。默认为 True ;
kernel_initializer 、 bias_initializer :权重矩阵 kernel 和偏置向量 bias 两个变量的初始化器。默认为 tf.glorot_uniform_initializer 1 。设置为 tf.zeros_initializer 表示将两个变量均初始化为全 0;
该层包含权重矩阵 kernel = [input_dim, units] 和偏置向量 bias = [units] 2 两个可训练变量,对应于 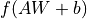 中的
中的 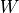 和
和 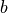 。
。
基础示例:多层感知机MLP
tf.keras.datasets tf.keras.datasets
tf.keras.datasetsnp.expand_dims()函数为图像数据手动在最后添加一维通道。tf.keras.Model 和 tf.keras.layers
class MLP(tf.keras.Model): def __init__(self): super().__init__() self.flatten = tf.keras.layers.Flatten() # Flatten层将除第一维(batch_size)以外的维度展平 self.dense1 = tf.keras.layers.Dense(units=100, activation=tf.nn.relu) self.dense2 = tf.keras.layers.Dense(units=10) def call(self, inputs): # [batch_size, 28, 28, 1] x = self.flatten(inputs) # [batch_size, 784] x = self.dense1(x) # [batch_size, 100] x = self.dense2(x) # [batch_size, 10] output = tf.nn.softmax(x) return output
输出 “输入图片分别属于 0 到 9 的概率”,也就是一个 10 维的离散概率分布
这个 10 维向量至少满足两个条件:
该向量中的每个元素均在 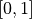 之间;
之间;
该向量的所有元素之和为 1。
softmax 函数能够凸显原始向量中最大的值,并抑制远低于最大值的其他分量
tf.keras.losses 和 tf.keras.optimizer
num_epochs = 5 batch_size = 50 learning_rate = 0.001

model = MLP() data_loader = MNISTLoader() optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate)

num_batches = int(data_loader.num_train_data // batch_size * num_epochs) for batch_index in range(num_batches): X, y = data_loader.get_batch(batch_size) with tf.GradientTape() as tape: y_pred = model(X) loss = tf.keras.losses.sparse_categorical_crossentropy(y_true=y, y_pred=y_pred) loss = tf.reduce_mean(loss) print("batch %d: loss %f" % (batch_index, loss.numpy())) grads = tape.gradient(loss, model.variables) optimizer.apply_gradients(grads_and_vars=zip(grads, model.variables))
从 DataLoader 中随机取一批训练数据;
将这批数据送入模型,计算出模型的预测值;
将模型预测值与真实值进行比较,计算损失函数(loss)。这里使用 tf.keras.losses中的交叉熵函数作为损失函数;
计算损失函数关于模型变量的导数;
将求出的导数值传入优化器,使用优化器的 apply_gradients 方法更新模型参数以最小化损失函数。
交叉熵作为损失函数,在分类问题中被广泛应用。其离散形式为 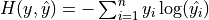 ,其中
,其中 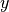 为真实概率分布,
为真实概率分布, 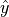 为预测概率分布,
为预测概率分布, 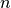 为分类任务的类别个数。预测概率分布与真实分布越接近,则交叉熵的值越小,反之则越大。
为分类任务的类别个数。预测概率分布与真实分布越接近,则交叉熵的值越小,反之则越大。
在 tf.keras 中,有两个交叉熵相关的损失函数 tf.keras.losses.categorical_crossentropy 和 tf.keras.losses.sparse_categorical_crossentropy 。其中 sparse 的含义是,真实的标签值 y_true 可以直接传入 int 类型的标签类别。具体而言:
loss = tf.keras.losses.sparse_categorical_crossentropy(y_true=y, y_pred=y_pred)
与
loss = tf.keras.losses.categorical_crossentropy(
y_true=tf.one_hot(y, depth=tf.shape(y_pred)[-1]),
y_pred=y_pred
)
的结果相同。
模型的评估: tf.keras.metrics

sparse_categorical_accuracy = tf.keras.metrics.SparseCategoricalAccuracy() num_batches = int(data_loader.num_test_data // batch_size) for batch_index in range(num_batches): start_index, end_index = batch_index * batch_size, (batch_index + 1) * batch_size y_pred = model.predict(data_loader.test_data[start_index: end_index]) sparse_categorical_accuracy.update_state(y_true=data_loader.test_label[start_index: end_index], y_pred=y_pred) print("test accuracy: %f" % sparse_categorical_accuracy.result())
update_state() 方法向评估器输入两个参数: y_pred 和 y_true ,即模型预测出的结果和真实结果。
包含一个或多个卷积层(Convolutional Layer)、池化层(Pooling Layer)和全连接层(Fully-connected Layer)

class CNN(tf.keras.Model): def __init__(self): super().__init__() self.conv1 = tf.keras.layers.Conv2D( filters=32, # 卷积层神经元(卷积核)数目 kernel_size=[5, 5], # 感受野大小 padding=‘same‘, # padding策略(vaild 或 same) activation=tf.nn.relu # 激活函数 ) self.pool1 = tf.keras.layers.MaxPool2D(pool_size=[2, 2], strides=2) self.conv2 = tf.keras.layers.Conv2D( filters=64, kernel_size=[5, 5], padding=‘same‘, activation=tf.nn.relu ) self.pool2 = tf.keras.layers.MaxPool2D(pool_size=[2, 2], strides=2) self.flatten = tf.keras.layers.Reshape(target_shape=(7 * 7 * 64,)) self.dense1 = tf.keras.layers.Dense(units=1024, activation=tf.nn.relu) self.dense2 = tf.keras.layers.Dense(units=10) def call(self, inputs): x = self.conv1(inputs) # [batch_size, 28, 28, 32] x = self.pool1(x) # [batch_size, 14, 14, 32] x = self.conv2(x) # [batch_size, 14, 14, 64] x = self.pool2(x) # [batch_size, 7, 7, 64] x = self.flatten(x) # [batch_size, 7 * 7 * 64] x = self.dense1(x) # [batch_size, 1024] x = self.dense2(x) # [batch_size, 10] output = tf.nn.softmax(x) return output
model = MLP() 更换成 model = CNN()即可
import tensorflow as tf import tensorflow_datasets as tfds num_batches = 1000 batch_size = 50 learning_rate = 0.001 dataset = tfds.load("tf_flowers", split=tfds.Split.TRAIN, as_supervised=True) dataset = dataset.map(lambda img, label: (tf.image.resize(img, [224, 224]) / 255.0, label)).shuffle(1024).batch(32) model = tf.keras.applications.MobileNetV2(weights=None, classes=5) optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate) for images, labels in dataset: with tf.GradientTape() as tape: labels_pred = model(images) loss = tf.keras.losses.sparse_categorical_crossentropy(y_true=labels, y_pred=labels_pred) loss = tf.reduce_mean(loss) print("loss %f" % loss.numpy()) grads = tape.gradient(loss, model.trainable_variables) optimizer.apply_gradients(grads_and_vars=zip(grads, model.trainable_variables))
model = tf.keras.applications.MobileNetV2() 实例化一个 MobileNetV2 网络结构
共通的常用参数如下:
input_shape :输入张量的形状(不含第一维的 Batch),大多默认为 224 × 224 × 3。一般而言,模型对输入张量的大小有下限,长和宽至少为 32 × 32 或 75 × 75 ;
include_top :在网络的最后是否包含全连接层,默认为 True ;
weights :预训练权值,默认为 ‘imagenet‘ ,即为当前模型载入在 ImageNet 数据集上预训练的权值。如需随机初始化变量可设为 None ;
classes :分类数,默认为 1000。修改该参数需要 include_top 参数为 True 且 weights 参数为 None 。
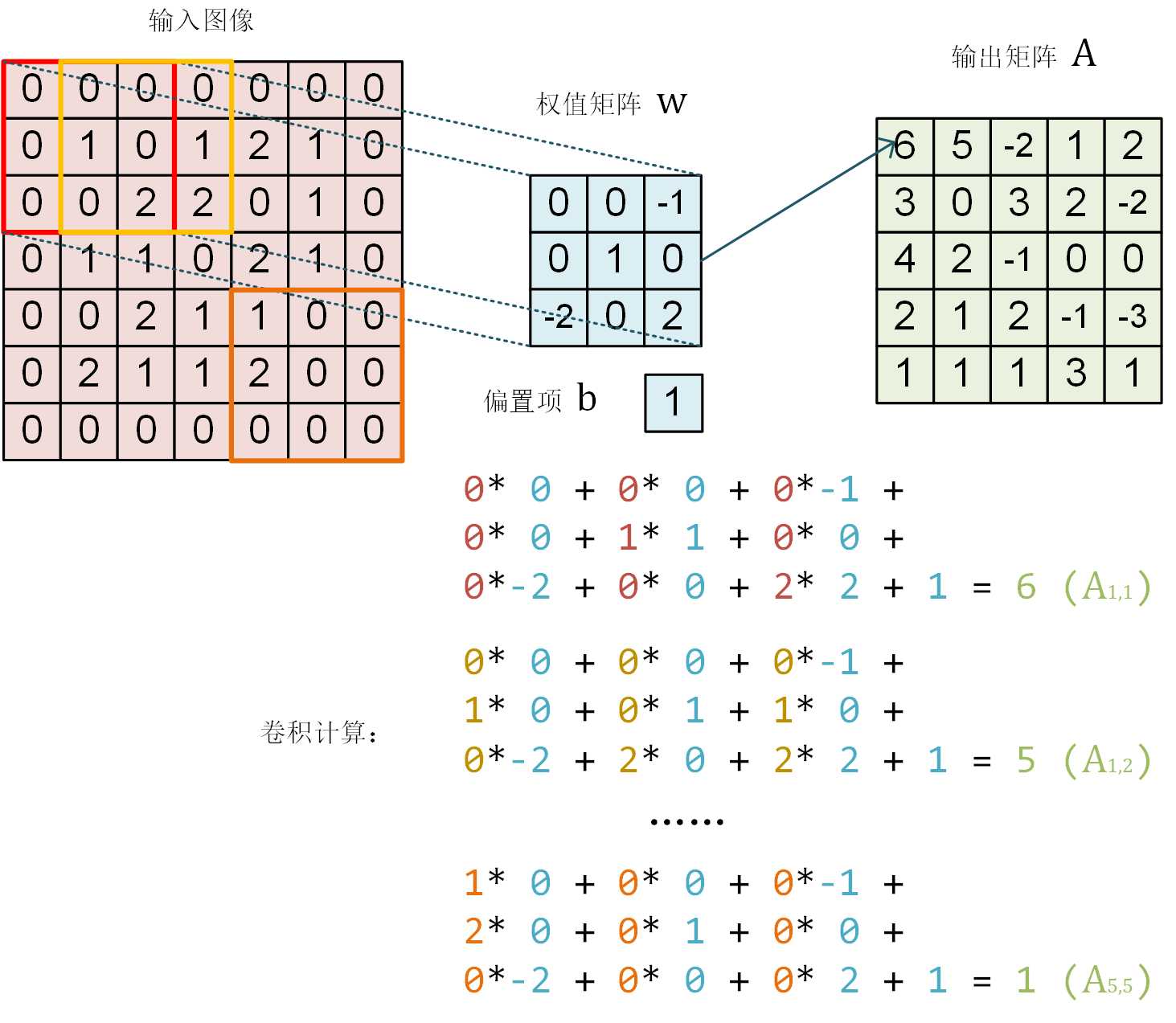
卷积示意图
一个单通道的 7×7 图像在通过一个感受野为 3×3 ,参数为 10 个的卷积层神经元后,得到 5×5 的矩阵
在 tf.keras.layers.Conv2D 中 padding 参数设为 same 时,会将周围缺少的部分使用 0 补齐,使得输出的矩阵大小和输入一致。
通过 tf.keras.layers.Conv2D 的 strides 参数即可设置步长(默认为 1)。比如,在上面的例子中,如果我们将步长设定为 2,输出的卷积结果即会是一个 3×3 的矩阵。
池化层(Pooling Layer)的理解则简单得多,其可以理解为对图像进行降采样的过程,对于每一次滑动窗口中的所有值,输出其中的最大值(MaxPooling)、均值或其他方法产生的值。
例如,对于一个三通道的 16×16 图像(即一个 16*16*3 的张量),经过感受野为 2×2,滑动步长为 2 的池化层,则得到一个 8*8*3 的张量。
适宜于处理序列数据的神经网络,被广泛用于语言模型、文本生成、机器翻译等
来看一下尼采风格文本的自动生成

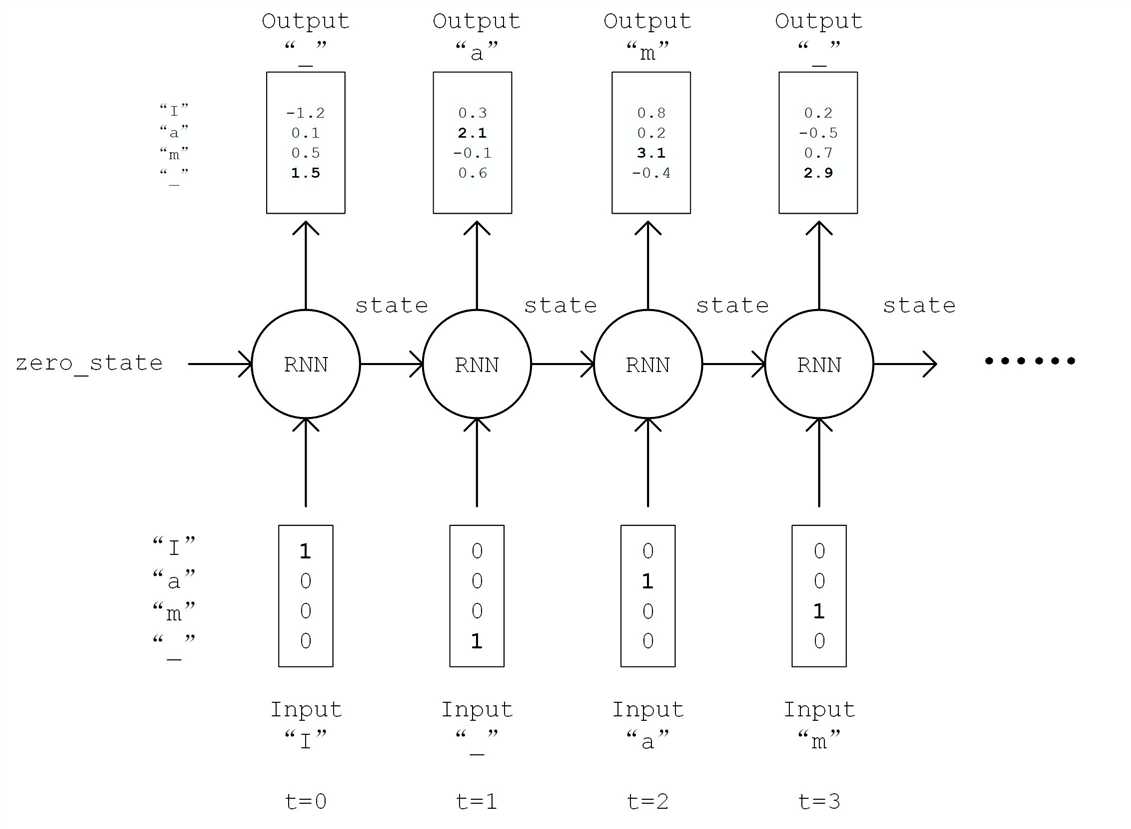
class DataLoader(): def __init__(self): path = tf.keras.utils.get_file(‘nietzsche.txt‘, origin=‘https://s3.amazonaws.com/text-datasets/nietzsche.txt‘) with open(path, encoding=‘utf-8‘) as f: self.raw_text = f.read().lower() self.chars = sorted(list(set(self.raw_text))) self.char_indices = dict((c, i) for i, c in enumerate(self.chars)) self.indices_char = dict((i, c) for i, c in enumerate(self.chars)) self.text = [self.char_indices[c] for c in self.raw_text] def get_batch(self, seq_length, batch_size): seq = [] next_char = [] for i in range(batch_size): index = np.random.randint(0, len(self.text) - seq_length) seq.append(self.text[index:index+seq_length]) next_char.append(self.text[index+seq_length]) return np.array(seq), np.array(next_char) # [batch_size, seq_length], [num_batch]
num_chars ,则每种字符赋予一个 0 到 num_chars - 1 之间的唯一整数编号 i
class RNN(tf.keras.Model): def __init__(self, num_chars, batch_size, seq_length): super().__init__() self.num_chars = num_chars self.seq_length = seq_length self.batch_size = batch_size self.cell = tf.keras.layers.LSTMCell(units=256) self.dense = tf.keras.layers.Dense(units=self.num_chars) def call(self, inputs, from_logits=False): inputs = tf.one_hot(inputs, depth=self.num_chars) # [batch_size, seq_length, num_chars] state = self.cell.get_initial_state(batch_size=self.batch_size, dtype=tf.float32) for t in range(self.seq_length): output, state = self.cell(inputs[:, t, :], state) logits = self.dense(output) if from_logits: return logits else: return tf.nn.softmax(logits)
__init__ 方法中我们实例化一个常用的 LSTMCell 单元,以及一个线性变换用的全连接层,我们首先对序列进行 “One Hot” 操作,即将序列中的每个字符的编码 i 均变换为一个 num_char 维向量,其第 i 位为 1,其余均为 0。变换后的序列张量形状为 [seq_length, num_chars] 。然后,我们初始化 RNN 单元的状态,存入变量 state 中。接下来,将序列从头到尾依次送入 RNN 单元,即在 t 时刻,将上一个时刻 t-1 的 RNN 单元状态 state 和序列的第 t 个元素 inputs[t, :] 送入 RNN 单元,得到当前时刻的输出 output 和 RNN 单元状态。取 RNN 单元最后一次的输出,通过全连接层变换到 num_chars 维,即作为模型的输出。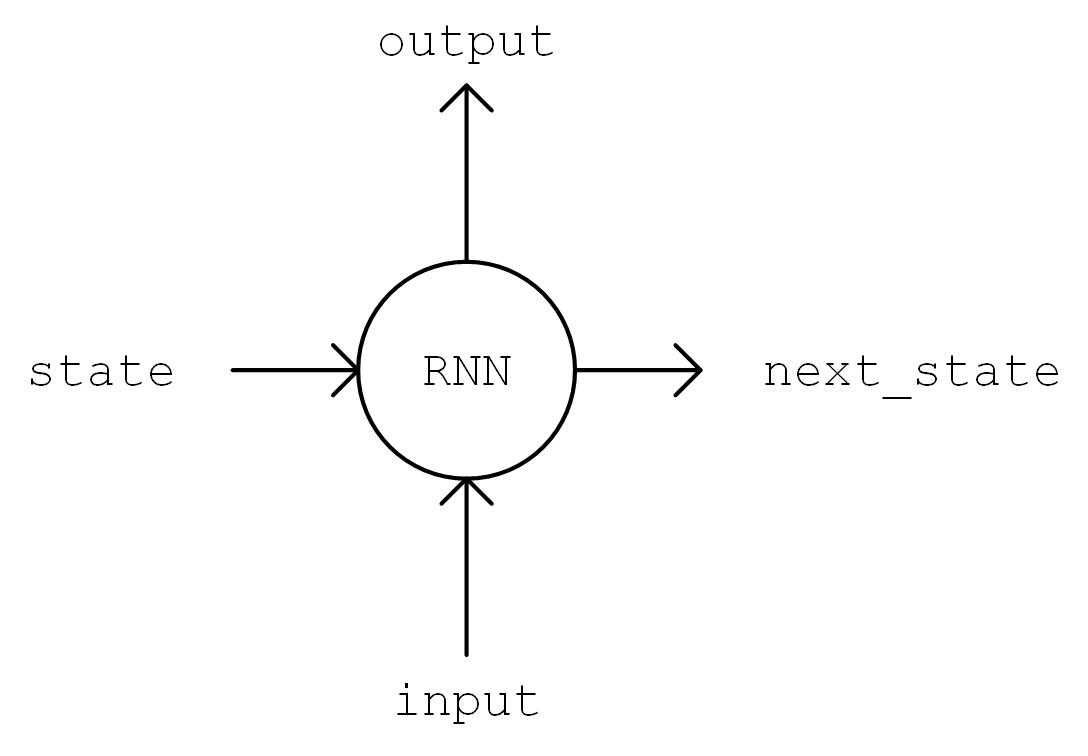

num_batches = 1000 seq_length = 40 batch_size = 50 learning_rate = 1e-3

data_loader = DataLoader() model = RNN(num_chars=len(data_loader.chars), batch_size=batch_size, seq_length=seq_length) optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate) for batch_index in range(num_batches): X, y = data_loader.get_batch(seq_length, batch_size) with tf.GradientTape() as tape: y_pred = model(X) loss = tf.keras.losses.sparse_categorical_crossentropy(y_true=y, y_pred=y_pred) loss = tf.reduce_mean(loss) print("batch %d: loss %f" % (batch_index, loss.numpy())) grads = tape.gradient(loss, model.variables) optimizer.apply_gradients(grads_and_vars=zip(grads, model.variables))
从 DataLoader 中随机取一批训练数据;
将这批数据送入模型,计算出模型的预测值;
将模型预测值与真实值进行比较,计算损失函数(loss);
计算损失函数关于模型变量的导数;
使用优化器更新模型参数以最小化损失函数。

def predict(self, inputs, temperature=1.): batch_size, _ = tf.shape(inputs) logits = self(inputs, from_logits=True) prob = tf.nn.softmax(logits / temperature).numpy() return np.array([np.random.choice(self.num_chars, p=prob[i, :]) for i in range(batch_size.numpy())]) X_, _ = data_loader.get_batch(seq_length, 1) for diversity in [0.2, 0.5, 1.0, 1.2]: X = X_ print("diversity %f:" % diversity) for t in range(400): y_pred = model.predict(X, diversity) print(data_loader.indices_char[y_pred[0]], end=‘‘, flush=True) X = np.concatenate([X[:, 1:], np.expand_dims(y_pred, axis=1)], axis=-1) print("\n")
tf.argmax() 函数,将对应概率最大的值作为预测值对于文本生成而言,这样的预测方式过于绝对,会使得生成的文本失去丰富性。np.random.choice() 函数按照生成的概率分布取样。这样,即使是对应概率较小的字符,也有机会被取样到。temperature 参数控制分布的形状,参数值越大则分布越平缓(最大值和最小值的差值越小),生成文本的丰富度越高;参数值越小则分布越陡峭,生成文本的丰富度越低。
强调如何基于环境而行动,以取得最大化的预期利益。
使用深度强化学习玩 CartPole(倒立摆)游戏

import gym env = gym.make(‘CartPole-v1‘) # 实例化一个游戏环境,参数为游戏名称 state = env.reset() # 初始化环境,获得初始状态 while True: env.render() # 对当前帧进行渲染,绘图到屏幕 action = model.predict(state) # 假设我们有一个训练好的模型,能够通过当前状态预测出这时应该进行的动作 next_state, reward, done, info = env.step(action) # 让环境执行动作,获得执行完动作的下一个状态,动作的奖励,游戏是否已结束以及额外信息 if done: # 如果游戏结束则退出循环 break

import tensorflow as tf import numpy as np import gym import random from collections import deque num_episodes = 500 # 游戏训练的总episode数量 num_exploration_episodes = 100 # 探索过程所占的episode数量 max_len_episode = 1000 # 每个episode的最大回合数 batch_size = 32 # 批次大小 learning_rate = 1e-3 # 学习率 gamma = 1. # 折扣因子 initial_epsilon = 1. # 探索起始时的探索率 final_epsilon = 0.01 # 探索终止时的探索率

class QNetwork(tf.keras.Model): def __init__(self): super().__init__() self.dense1 = tf.keras.layers.Dense(units=24, activation=tf.nn.relu) self.dense2 = tf.keras.layers.Dense(units=24, activation=tf.nn.relu) self.dense3 = tf.keras.layers.Dense(units=2) def call(self, inputs): x = self.dense1(inputs) x = self.dense2(x) x = self.dense3(x) return x def predict(self, inputs): q_values = self(inputs) return tf.argmax(q_values, axis=-1)

if __name__ == ‘__main__‘: env = gym.make(‘CartPole-v1‘) # 实例化一个游戏环境,参数为游戏名称 model = QNetwork() optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate) replay_buffer = deque(maxlen=10000) # 使用一个 deque 作为 Q Learning 的经验回放池 epsilon = initial_epsilon for episode_id in range(num_episodes): state = env.reset() # 初始化环境,获得初始状态 epsilon = max( # 计算当前探索率 initial_epsilon * (num_exploration_episodes - episode_id) / num_exploration_episodes, final_epsilon) for t in range(max_len_episode): env.render() # 对当前帧进行渲染,绘图到屏幕 if random.random() < epsilon: # epsilon-greedy 探索策略,以 epsilon 的概率选择随机动作 action = env.action_space.sample() # 选择随机动作(探索) else: action = model.predict(np.expand_dims(state, axis=0)).numpy() # 选择模型计算出的 Q Value 最大的动作 action = action[0] # 让环境执行动作,获得执行完动作的下一个状态,动作的奖励,游戏是否已结束以及额外信息 next_state, reward, done, info = env.step(action) # 如果游戏Game Over,给予大的负奖励 reward = -10. if done else reward # 将(state, action, reward, next_state)的四元组(外加 done 标签表示是否结束)放入经验回放池 replay_buffer.append((state, action, reward, next_state, 1 if done else 0)) # 更新当前 state state = next_state if done: # 游戏结束则退出本轮循环,进行下一个 episode print("episode %d, epsilon %f, score %d" % (episode_id, epsilon, t)) break if len(replay_buffer) >= batch_size: # 从经验回放池中随机取一个批次的四元组,并分别转换为 NumPy 数组 batch_state, batch_action, batch_reward, batch_next_state, batch_done = zip( *random.sample(replay_buffer, batch_size)) batch_state, batch_reward, batch_next_state, batch_done = [np.array(a, dtype=np.float32) for a in [batch_state, batch_reward, batch_next_state, batch_done]] batch_action = np.array(batch_action, dtype=np.int32) q_value = model(batch_next_state) y = batch_reward + (gamma * tf.reduce_max(q_value, axis=1)) * (1 - batch_done) # 计算 y 值 with tf.GradientTape() as tape: loss = tf.keras.losses.mean_squared_error( # 最小化 y 和 Q-value 的距离 y_true=y, y_pred=tf.reduce_sum(model(batch_state) * tf.one_hot(batch_action, depth=2), axis=1) ) grads = tape.gradient(loss, model.variables) optimizer.apply_gradients(grads_and_vars=zip(grads, model.variables)) # 计算梯度并更新参数
QNetwork 更换为 CNN 网络,并对状态做一些修改,即可用于玩一些简单的视频游戏
以上示例均使用了 Keras 的 Subclassing API 建立模型,即对 tf.keras.Model 类进行扩展以定义自己的新模型,同时手工编写了训练和评估模型的流程。
只需要建立一个结构相对简单和典型的神经网络(比如上文中的 MLP 和 CNN),并使用常规的手段进行训练。这时,Keras 也给我们提供了另一套更为简单高效的内置方法来建立、训练和评估模型。

model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(), tf.keras.layers.Dense(100, activation=tf.nn.relu), tf.keras.layers.Dense(10), tf.keras.layers.Softmax() ])
tf.keras.models.Sequential() 提供一个层的列表,就能快速地建立一个 tf.keras.Model 模型并返回
inputs = tf.keras.Input(shape=(28, 28, 1)) x = tf.keras.layers.Flatten()(inputs) x = tf.keras.layers.Dense(units=100, activation=tf.nn.relu)(x) x = tf.keras.layers.Dense(units=10)(x) outputs = tf.keras.layers.Softmax()(x) model = tf.keras.Model(inputs=inputs, outputs=outputs)
tf.keras.Model 的 inputs 和 outputs 参数
model.compile( optimizer=tf.keras.optimizers.Adam(learning_rate=0.001), loss=tf.keras.losses.sparse_categorical_crossentropy, metrics=[tf.keras.metrics.sparse_categorical_accuracy] )
接受 3 个重要的参数:
oplimizer:优化器,可从tf.keras.optimizers中选择;
loss:损失函数,可从tf.keras.losses中选择;
metrics:评估指标,可从tf.keras.metrics中选择

model.fit(data_loader.train_data, data_loader.train_label, epochs=num_epochs, batch_size=batch_size)
接受 5 个重要的参数:
x:训练数据;
y:目标数据(数据标签);
epochs:将训练数据迭代多少遍;
batch_size:批次的大小;
validation_data:验证数据,可用于在训练过程中监控模型的性能。

print(model.evaluate(data_loader.test_data, data_loader.test_label))
如果现有的这些层无法满足我的要求,我需要定义自己的层怎么办?
事实上,不仅可以继承 tf.keras.Model 编写自己的模型类,也可以继承 tf.keras.layers.Layer 编写自己的层。

class MyLayer(tf.keras.layers.Layer): def __init__(self): super().__init__() # 初始化代码 def build(self, input_shape): # input_shape 是一个 TensorShape 类型对象,提供输入的形状 # 在第一次使用该层的时候调用该部分代码,在这里创建变量可以使得变量的形状自适应输入的形状 # 而不需要使用者额外指定变量形状。 # 如果已经可以完全确定变量的形状,也可以在__init__部分创建变量 self.variable_0 = self.add_weight(...) self.variable_1 = self.add_weight(...) def call(self, inputs): # 模型调用的代码(处理输入并返回输出) return output
tf.keras.layers.Layer 类,并重写 __init__ 、 build 和 call 三个方法
class LinearLayer(tf.keras.layers.Layer): def __init__(self, units): super().__init__() self.units = units def build(self, input_shape): # 这里 input_shape 是第一次运行call()时参数inputs的形状 self.w = self.add_variable(name=‘w‘, shape=[input_shape[-1], self.units], initializer=tf.zeros_initializer()) self.b = self.add_variable(name=‘b‘, shape=[self.units], initializer=tf.zeros_initializer()) def call(self, inputs): y_pred = tf.matmul(inputs, self.w) + self.b return y_pred
build 方法中创建两个变量,并在 call 方法中使用创建的变量进行运算
class LinearModel(tf.keras.Model): def __init__(self): super().__init__() self.layer = LinearLayer(units=1) def call(self, inputs): output = self.layer(inputs) return output

class MeanSquaredError(tf.keras.losses.Loss): def call(self, y_true, y_pred): return tf.reduce_mean(tf.square(y_pred - y_true))
tf.keras.losses.Loss 类,重写 call 方法即可,输入真实值 y_true 和模型预测值 y_pred ,输出模型预测值和真实值之间通过自定义的损失函数计算出的损失值。上面的示例为均方差损失函数

class SparseCategoricalAccuracy(tf.keras.metrics.Metric): def __init__(self): super().__init__() self.total = self.add_weight(name=‘total‘, dtype=tf.int32, initializer=tf.zeros_initializer()) self.count = self.add_weight(name=‘count‘, dtype=tf.int32, initializer=tf.zeros_initializer()) def update_state(self, y_true, y_pred, sample_weight=None): values = tf.cast(tf.equal(y_true, tf.argmax(y_pred, axis=-1, output_type=tf.int32)), tf.int32) self.total.assign_add(tf.shape(y_true)[0]) self.count.assign_add(tf.reduce_sum(values)) def result(self): return self.count / self.total
tf.keras.metrics.Metric 类,并重写 __init__ 、 update_state 和 result 三个方法。上面的示例对前面用到的 SparseCategoricalAccuracy评估指标类做了一个简单的重实现:
三分钟快速上手TensorFlow 2.0 (上)——前置基础、模型建立与可视化
原文:https://www.cnblogs.com/xingnie/p/12337709.html