把一本《白话深度学习与tensorflow》给啃完了,了解了一下基本的BP网络,CNN,RNN这些。感觉实际上算法本身不是特别的深奥难懂,最简单的BP网络基本上学完微积分和概率论就能搞懂,CNN引入的卷积,池化等也是数字图像处理中比较成熟的理论,RNN使用的数学工具相对而言比较高深一些,需要再深入消化消化,最近也在啃白皮书,争取从数学上把这些理论吃透
当然光学理论不太行,还是得要有一些实践的,下面是三个入门级别的,可以用来辅助对BP网络的理解
入门:tensorflow线性回归
https://zhuanlan.zhihu.com/p/37368943
代码:
from?__future__?import??print_function
import?tensorflow?as?tf
import?numpy
import?matplotlib.pyplot?as?plt
rng?=?numpy.random
#?Parameters
learning_rate?=?0.01
training_epochs?=?1000
display_step?=?50
save_step?=?500
#?Training?Data
train_X?=?numpy.asarray([3.3,?4.4,?5.5,?6.71,?6.93,?4.168,?9.779,?6.182,?7.59,?2.167,
?????????????????????????7.042,?10.791,?5.313,?7.997,?5.654,?9.27,?3.1])
train_Y?=?numpy.asarray([3,?4.7,?5,?7.21,?6.93,?4.168,?9.779,?6.182,?7.59,?2.167,
?????????????????????????7.042,?10.291,?5.813,?7.997,?5.654,?9.17,?3.2])
#?define?graph?input
X?=?tf.placeholder(dtype=tf.float32,?name="X")
Y?=?tf.placeholder(dtype=tf.float32,?name="Y")
with?tf.variable_scope("linear_regression"):
????#?set?model?weight
????W?=?tf.get_variable(initializer=rng.randn(),?name="weight")
????b?=?tf.get_variable(initializer=rng.randn(),?name="bias")
????#?Construct?a?linear?model
????mul?=?tf.multiply(X,?W,?name="mul")
????pred?=?tf.add(mul,?b,?name="pred")
#?L2?loss
with?tf.variable_scope("l2_loss"):
????loss?=?tf.reduce_mean(tf.pow(pred-Y,?2))
#?Gradient?descent
train_op?=?tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
#?Initialize?the?variables
init_op?=?tf.global_variables_initializer()
#?Checkpoint?save?path
ckpt_path?=?'./ckpt/linear-regression-model.ckpt'
#?create?a?saver
saver?=?tf.train.Saver()
#?Summary?save?path
summary_path?=?'./ckpt/'
#?Create?a?summary?to?monitor?tensors?which?you?want?to?show?in?tensorboard
tf.summary.scalar('weight',?W)
tf.summary.scalar('bias',?b)
tf.summary.scalar('loss',?loss)
#?Merges?all?summaries?collected?in?the?default?graph
merge_summary_op?=?tf.summary.merge_all()
#?Start?training
with?tf.Session()?as?sess:
????summary_writer?=?tf.summary.FileWriter(summary_path,?sess.graph)
????#?Run?the?initializer
????sess.run(init_op)
????#?Fit?all?training?data
????for?epoch?in?range(training_epochs):
????????for?(x,?y)?in?zip(train_X,?train_Y):
????????????#?Do?feed?dict
????????????_,?summary?=?sess.run([train_op,?merge_summary_op],?feed_dict={X:?x,?Y:?y})
????????if?(epoch?+?1)?%?save_step?==?0:
????????????#?Do?save?model
????????????save_path?=?saver.save(sess,?ckpt_path,?global_step=epoch)
????????????print("Model?saved?in?file?%s"?%?save_path)
????????if?(epoch?+?1)?%?display_step?==?0:
????????????#?Display?loss?and?value
????????????c?=?sess.run(loss,?feed_dict={X:?train_X,?Y:?train_Y})
????????????print("Epoch:",?"%04d"?%?(epoch+1),?"loss=",?"{:.9f}".format(c),
??????????????????"W=",?W.eval(),?"b=",?b.eval())
????????????#?Add?variable?state?to?summary?file
????????????summary_writer.add_summary(summary,?global_step=epoch)
????print("Optimization?finished")
????#?Save?the?final?model
????summary_writer.close()
????#?Calculate?final?loss?after?training
????training_loss?=?sess.run(loss,?feed_dict={X:?train_X,?Y:?train_Y})
????print("Training?loss=",?training_loss,?"W=",?sess.run(W),?"b=",?sess.run(b),?'\n')
????plt.plot(train_X,?train_Y,?'ro',?label='Origin?data')
????plt.plot(train_X,?sess.run(W)?*?train_X?+?sess.run(b),?label='fitted?line')
????plt.legend()
????plt.show()
使用tensorboard的方法:
tensorboard --logdir=./ckpt/ (程序中存储summary的地址)然后在浏览器输入
127.0.0.1:6006
即可查看
我训练的时候出现过loss不降反升的问题,说明选择的学习率有问题

除了学习率之外,学习的效果和优化算法的选择也有关系,我一开始选择的是梯度下降算法
train_op = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss) 但是效果很不好
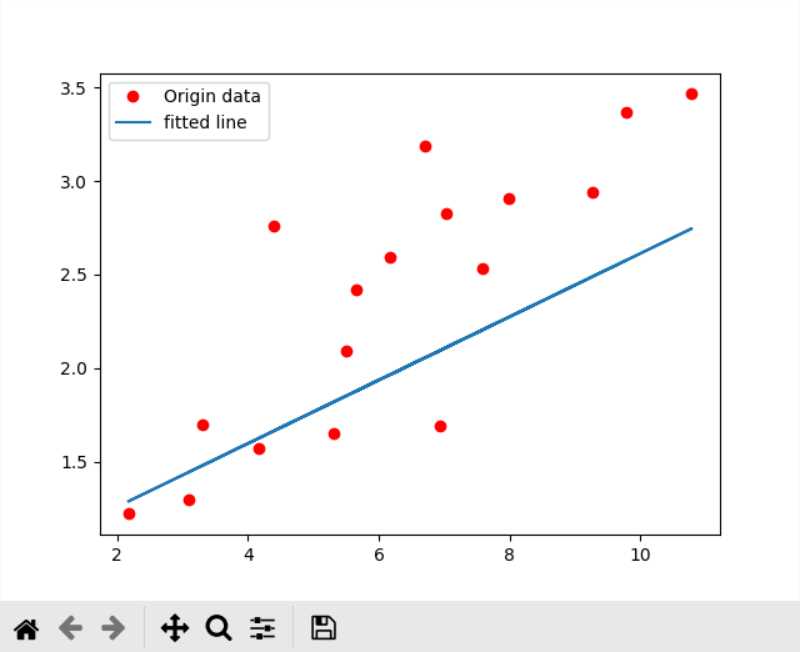
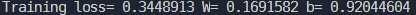
而更换优化算法为
train_op = tf.train.AdamOptimizer(learning_rate).minimize(loss)效果好了不少
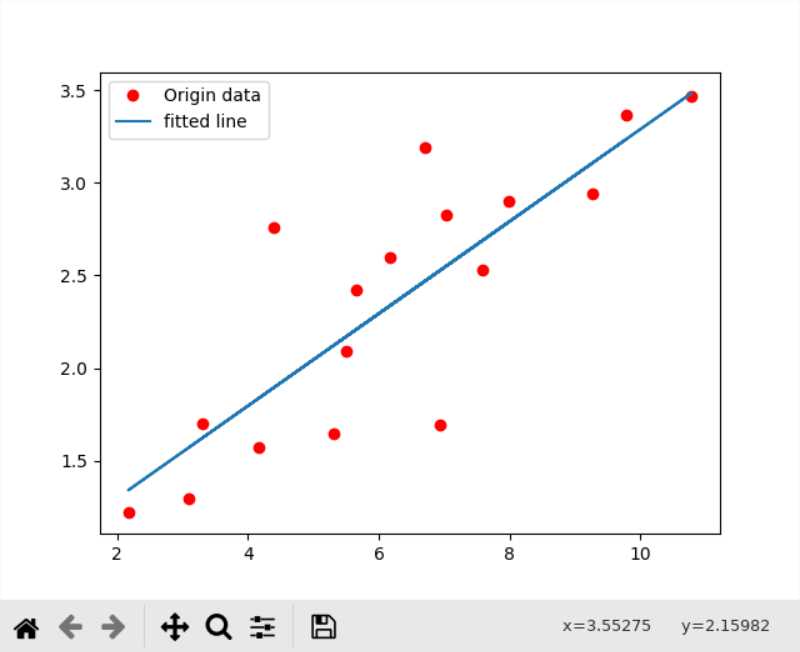
loss也比梯度下降小了一倍多
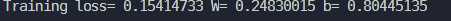
关于各个梯度算法的介绍
https://ruder.io/optimizing-gradient-descent/index.html
https://zhuanlan.zhihu.com/p/22252270
SGD(随机梯度下降)的缺点:
由于从头至尾使用的学习率完全一致,难以选择合适的学习率
容易困于鞍点(可以通过合适的初始化和step size克服)
而Adam算法通过引入梯度的一阶矩和二阶矩估计,引入了近似于动量和摩擦力的物理性质,使得训练具有了自适应性,所以比单纯的梯度下降往往要好用一些。


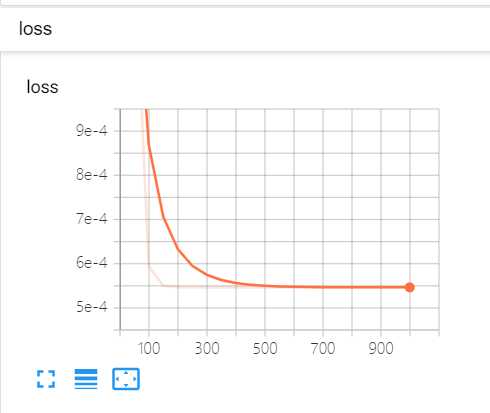
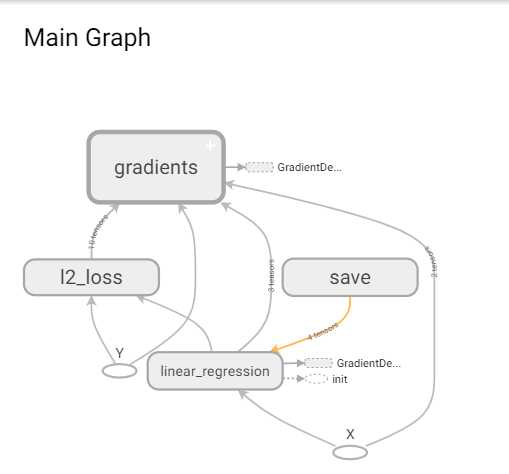
借助tensorboard可视化的观察loss,bias和weight的变化还是比较方便的,另外查看graph的功能也很好用
使用checkpoint保存的模型:
1.定义一个一模一样的graph,然后导入,可以发现创建图的过程和线性回归的代码一模一样的,创建完毕之后最关键的就是创建tf.train.Saver(),然后调用Saver类下面的restore方法,参数一个是sess一个是ckpt文件的路径
2.直接导入meta文件,这样可以将graph和参数一起导入
1.代码
from?__future__?import?print_function
import?tensorflow?as?tf
import?matplotlib.pyplot?as?plt
import?numpy
rng?=?numpy.random
X?=?tf.placeholder(dtype=tf.float32,?name="X")
Y?=?tf.placeholder(dtype=tf.float32,?name="Y")
with?tf.variable_scope("linear_regression"):
????W?=?tf.Variable(rng.randn(),?name="weight")
????b?=?tf.Variable(rng.randn(),?name="bias")
????mul?=?tf.multiply(X,?W,?name="mul")
????pred?=?tf.add(mul,?b,?name="pred")
saver?=?tf.train.Saver()
ckpt_path?=?'./ckpt/linear-regression-model.ckpt-999'
with?tf.Session()?as?sess:
????saver.restore(sess,?ckpt_path)
????print('Restored?Value?W={},?b={}'.format(W.eval(),b.eval()))结果:
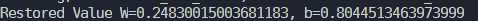
2.代码
采用import_meta_graph导入graph,需要筑起启动Session时要设置参数config=config
调用graph中的tensor时可以直接使用graph.get_tensor_by_name
from __future__ import print_function
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy
config = tf.ConfigProto(allow_soft_placement=True)
*# path of the .meta file*
ckpt = './ckpt/linear-regression-model.ckpt-999'
with tf.Session(config=config) as sess:
saver = tf.train.import_meta_graph(ckpt + '.meta')
saver.restore(sess, ckpt)
graph = sess.graph
X = graph.get_tensor_by_name("X:0")
pred = graph.get_tensor_by_name("linear_regression/pred:0")
W = graph.get_tensor_by_name("linear_regression/weight:0")
b = graph.get_tensor_by_name("linear_regression/bias:0")
print('Restored value W={}, b={}'.format(W.eval(), b.eval()))结果:

https://blog.csdn.net/y12345678904/article/details/77743696
线性回归中使用的multiply(),但是由于实际使用中都是矩阵相乘,所以matmul更加的常用一些
tf.matmul() 和tf.multiply() 的区别
1.tf.multiply()两个矩阵中对应元素各自相乘
格式: tf.multiply(x, y, name=None)
参数:
x: 一个类型为:half, float32, float64, uint8, int8, uint16, int16, int32, int64, complex64, complex128的张量。
y: 一个类型跟张量x相同的张量。
返回值: x * y element-wise.
注意:
(1)multiply这个函数实现的是元素级别的相乘,也就是两个相乘的数元素各自相乘,而不是矩阵乘法,注意和tf.matmul区别。
(2)两个相乘的数必须有相同的数据类型,不然就会报错。
2.tf.matmul()将矩阵a乘以矩阵b,生成a * b。
格式: tf.matmul(a, b, transpose_a=False, transpose_b=False, adjoint_a=False, adjoint_b=False, a_is_sparse=False, b_is_sparse=False, name=None)
参数:
a: 一个类型为 float16, float32, float64, int32, complex64, complex128 且张量秩 > 1 的张量。
b: 一个类型跟张量a相同的张量。
transpose_a: 如果为真, a则在进行乘法计算前进行转置。
transpose_b: 如果为真, b则在进行乘法计算前进行转置。
adjoint_a: 如果为真, a则在进行乘法计算前进行共轭和转置。
adjoint_b: 如果为真, b则在进行乘法计算前进行共轭和转置。
a_is_sparse: 如果为真, a会被处理为稀疏矩阵。
b_is_sparse: 如果为真, b会被处理为稀疏矩阵。
name: 操作的名字(可选参数)
返回值: 一个跟张量a和张量b类型一样的张量且最内部矩阵是a和b中的相应矩阵的乘积。
注意:
(1)输入必须是矩阵(或者是张量秩 >2的张量,表示成批的矩阵),并且其在转置之后有相匹配的矩阵尺寸。
(2)两个矩阵必须都是同样的类型,支持的类型如下:float16, float32, float64, int32, complex64, complex128。
代码:
import?tensorflow?as?tf
import?numpy?as?np
import?matplotlib.pyplot?as?plt
learning_rate?=?0.1
training_epochs?=?20000
display_step?=?500
x_data?=?np.linspace(-1,1,200)
x_data?=?x_data.reshape((200,1))
noise?=?np.random.normal(0,?0.05,?x_data.shape)
y_data?=?np.square(x_data)?+?noise
x?=?tf.placeholder(tf.float32,?[200,1])
y?=?tf.placeholder(tf.float32,?[200,1])
#?hidden?layer
weights_l1?=?tf.Variable(tf.random_normal([1,?10]))
biases_l1?=?tf.Variable(tf.zeros([1,?10]))
wx_plus_b_l1?=?tf.matmul(x,?weights_l1)?+?biases_l1
l1?=?tf.nn.tanh(wx_plus_b_l1)
#?output?layer
weights_l2?=?tf.Variable(tf.random_normal([10,1]))
biases_l2?=?tf.Variable(tf.zeros([1,1]))
wx_plus_b_l2?=?tf.matmul(l1,?weights_l2)?+?biases_l2
prediction?=?tf.nn.tanh(wx_plus_b_l2)
#?loss?function
loss?=?tf.reduce_mean(tf.square(y?-?prediction))
#?gradient?descent
train_step?=?tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
with?tf.Session()?as?sess:
????sess.run(tf.global_variables_initializer())
????for?global_epochs?in?range(training_epochs):
????????sess.run(train_step,?feed_dict={x:x_data,?y:y_data})
????????if?(global_epochs?+?1)?%?display_step?==?0:
????????????loss_value?=?sess.run(loss,?feed_dict={x:x_data,?y:y_data})
????????????print("epoch:",?"%04d"?%(global_epochs?+?1),?"loss=",?"{:.9f}".format(loss_value))?
????prediction_value?=?sess.run(prediction,?feed_dict={x:x_data})
????plt.figure()
????plt.scatter(x_data,?y_data)
????plt.plot(x_data,?prediction_value,'r-',lw=3)
????plt.show()
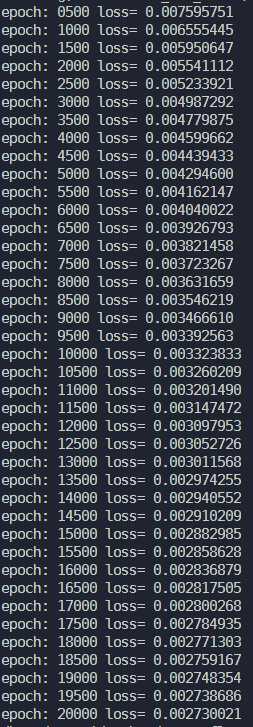
结果:
下降的效果还是比较明显的,从0.0076一直下降到了0.0027
图像:
Gradient Descent的结果,比较符合二次曲线的分布规律
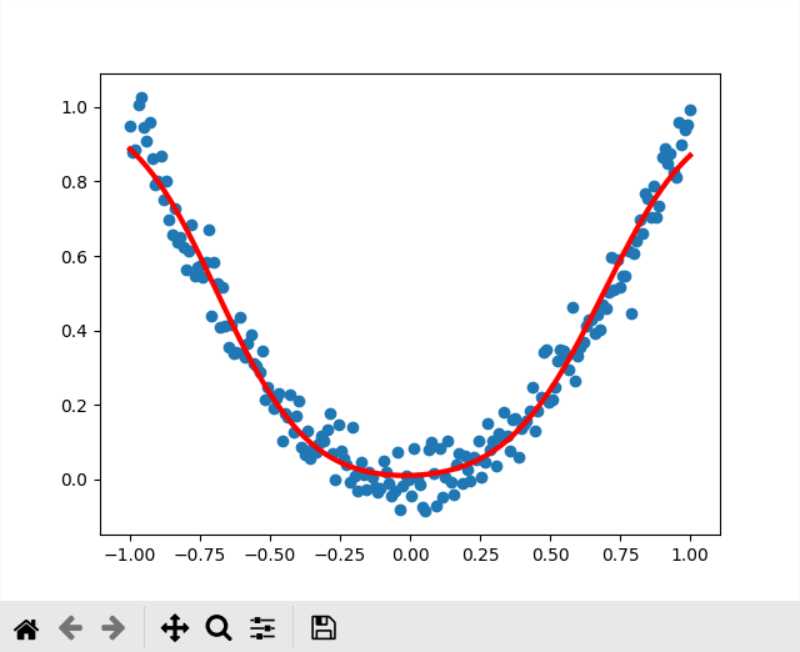
Adam的结果,虽然loss比Gradient Descent小,但是实际上有比较明显的过拟合了

另外这里的激活函数采用的是tanh,更换成sigmoid之后
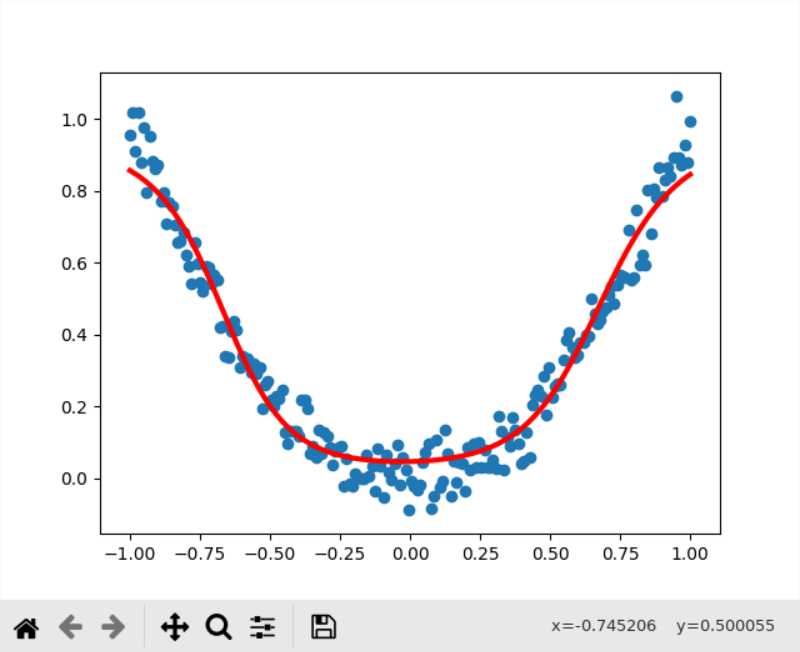

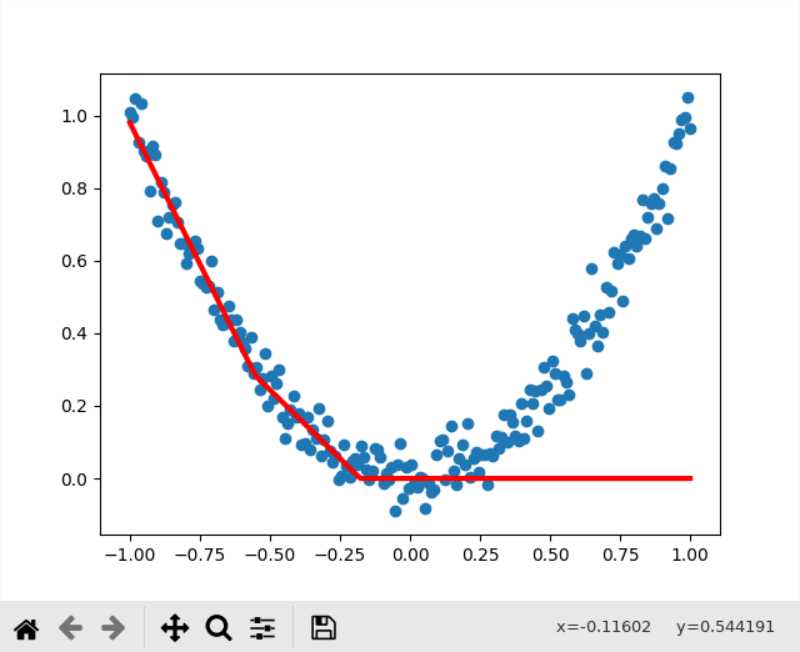
效果差于tanh做激活函数,因为tanh的导数值大于sigmoid,收敛速度实际上是快于sigmoid的,不过我把训练次数翻到了40000次后发现好像sigmoid作为激活函数,训练的上限就是0.004几了,而如果采用ReLU的话,就直接起飞了,根本无法收敛
ReLU还是适合在深度网络中做激活函数,在这种就一层的网络里面来搞效果就比较差(本来的目的就是为了解决深度网络中的梯度爆炸)
https://geektutu.com/post/tensorflow-mnist-simplest.html
分为一个mnist_model.py用于构建网络,一个mnist_train.py用于训练,这种构建方式是大多数神经网络都会采取的方式
一维向量既可以用[1, 维数]来表示,也可以用[None, 维数]来表示
l由于label采用了1-10的独热编码,loss函数使用的是交叉熵,公式为(p为真实分布,q为非真实分布)
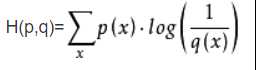
代码为
self.loss = -tf.reduce_sum(self.label * tf.log(self.y + 1e-10))这里加1e-10的目的是为了防止y=0时出现数值溢出错误
关于feed_dict
sess.run() 中的feed_dict

结果是1,本质上就是一个临时赋值的功能
model的代码:
import?tensorflow?as?tf
class?Network:
????def?__init__(self):
????????#?learning?rate
????????self.learning_rate?=?0.01
????????#?input?tensor
????????self.x?=?tf.placeholder(tf.float32,?[None,?784])
????????#?label?tensor
????????self.label?=?tf.placeholder(tf.float32,?[None,?10])
????????#?weight
????????self.w?=?tf.Variable(tf.random_normal([784,?10]))
????????#?bias
????????self.b?=?tf.Variable(tf.random_normal([10]))
????????#?output?tensor
????????self.y?=?tf.nn.softmax(tf.matmul(self.x,?self.w)?+?self.b)
????????#?loss
????????self.loss?=?-tf.reduce_sum(self.label?*?tf.log(self.y?+?1e-10))
????????#?train
????????self.train?=?tf.train.GradientDescentOptimizer(self.learning_rate).minimize(self.loss)
????????#?verify
????????predict?=?tf.equal(tf.arg_max(self.label,?1),?tf.arg_max(self.y,?1))
????????#?calc?the?accuracy
????????self.accuracy?=?tf.reduce_mean(tf.cast(predict,?"float"))train的代码:
train的代码
import?tensorflow?as?tf
from?tensorflow.examples.tutorials.mnist?import?input_data
from?mnist_model?import?Network
class?Train:
????def?__init__(self):
????????self.net?=?Network()
????????#?initialize?session
????????self.sess?=?tf.Session()
????????#?initialize?variables
????????self.sess.run(tf.global_variables_initializer())
????????#?input?data
????????self.data?=?input_data.read_data_sets('/home/satori/python/tensorflow_test/data_set',?one_hot=True)
????????#?create?a?saver
????????self.saver?=?tf.train.Saver()
????def?train(self):
????????batch_size?=?64
????????train_epoch?=?10000
????????save_interval?=?1000
????????display_interval?=?100
????????ckpt_path?=?'./ckpt/mnist-model.ckpt'
????????for?step?in?range(train_epoch):
????????????x,?label?=?self.data.train.next_batch(batch_size)
????????????#?training
????????????self.sess.run(self.net.train,?feed_dict={self.net.x:x,?self.net.label:label})
????????????if?(step?+?1)?%?display_interval?==?0:
????????????????#?print?the?loss
????????????????loss?=?self.sess.run(self.net.loss,?feed_dict={self.net.x:x,?self.net.label:label})
????????????????print("step=%d,?loss=%.2f"?%((step+1),?loss))
????????????
????????????if?(step?+?1)?%?save_interval?==?0:
????????????????#?save?the?model
????????????????self.saver.save(self.sess,?ckpt_path,?global_step=step)
????????????????print("model?saved?in?file?%s"?%ckpt_path)
????def?calculate_accuracy(self):
????????test_x?=?self.data.test.images
????????test_label?=?self.data.test.labels
????????#?using?the?net?trained
????????accuracy?=?self.sess.run(self.net.accuracy,?feed_dict={self.net.x:?test_x,?self.net.label:?test_label})
????????print("accuracy=%.2f,%dof?pictures?are?tested"?%(accuracy,len(test_label)))
????
if?__name__?==?"__main__":
????app?=?Train()
????app.train()
????app.calculate_accuracy()
train中会保存模型,然后我们需要将模型导入predict,对样本进行识别
import?numpy?as?np
import?tensorflow?as?tf
from?PIL?import?Image
from?mnist_model?import?Network
ckpt_path?=?'./ckpt/mnist-model.ckpt-9999'
class?Predict:
????def?__init__(self):
????????#?restore?the?network
????????self.net?=?Network()
????????self.sess?=?tf.Session()
????????self.sess.run(tf.global_variables_initializer())
????????self.restore()
????def?restore(self):
????????saver?=?tf.train.Saver()
????????saver.restore(self.sess,?ckpt_path)
????def?predict(self,?image_path):
????????#?turn?image?into?black?and?white
????????img?=?Image.open(image_path).convert('L')
????????flatten_img?=?np.reshape(img,?784)
????????x?=?np.array([1?-?flatten_img])
????????y?=?self.sess.run(self.net.y,?feed_dict={self.net.x:?x})
????????
????????print(image_path)
????????print('??????????->?Predict?digit',?np.argmax(y[0]))
if?__name__?==?"__main__":
????app?=?Predict()
????app.predict('./test_images/0.png')
????app.predict('./test_images/1.png')
????app.predict('./test_images/4.png')
样本:

运行结果:
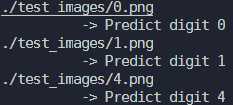
另外在导入模型方面,还可以引入
def restore(self):
saver = tf.train.Saver()
ckpt = tf.train.get_checkpoint_state(CKPT_DIR)
if ckpt and ckpt.model_checkpoint_path:
saver.restore(self.sess, ckpt.model_checkpoint_path)
else:
raise FileNotFoundError("未保存任何模型")进行错误处理
实际上还是可以像线性回归那边一样加入一个summary来方便用tensorboard来可视化,不过因为我上面跑的还挺成功的,就先不搞这个了,总体上还是比较顺利的
机器学习入门实践——线性回归&非线性回归&mnist手写体识别
原文:https://www.cnblogs.com/sasasatori/p/12342134.html