以左为尊,根据根结点的所在顺序,将二叉树的遍历分为三种:
先序遍历:根左右,根在先。
中序遍历:左根右,根在中。
后序遍历:左右根,根在后。
小结
二叉查找树:又叫二叉搜索树或二叉排序树。它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉树。 中序遍历可以得到顺序的结点值。
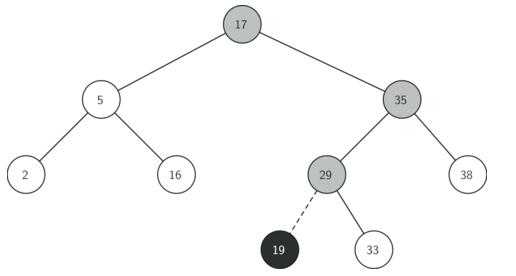
平衡二叉树,又称AVL树,指的是左子树上的所有节点的值都比根节点的值小,而右子树上的所有节点的值都比根节点的值大,且左子树与右子树的高度差最大为1。因此,平衡二叉树满足所有二叉排序(搜索)树的性质。至于AVL,则是取自两个发明平衡二叉树的科学家的名字:G. M. Adelson-Velsky和E. M. Landis。
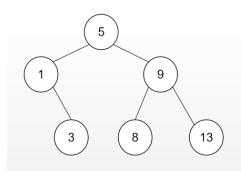
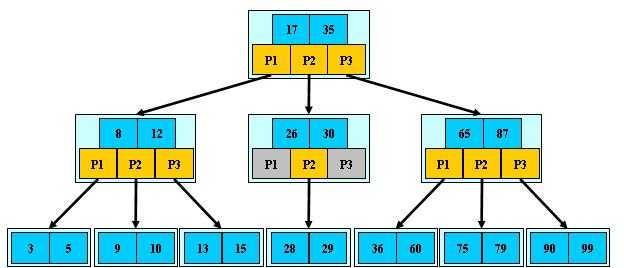
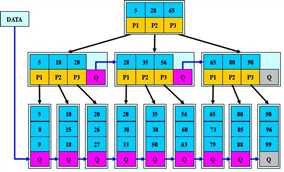
B树:多路搜索树,每个结点存储M/2到M个关键字,非叶子结点存储指向关键 字范围的子结点;所有关键字在整颗树中出现,且只出现一次,非叶子结点可以命中;
B+树:在B树基础上,为叶子结点增加链表指针,所有关键字都在叶子结点中出现,非叶子结点作为叶子结点的索引;B+树总是到叶子结点才命中;
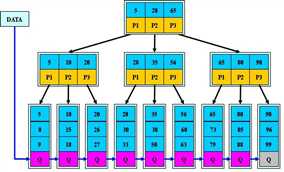
B*树:在B+树基础上,为非叶子结点也增加链表指针,将结点的最低利用率从1/2提高到2/3;
原文:https://www.cnblogs.com/shijianchuzhenzhi/p/12348869.html