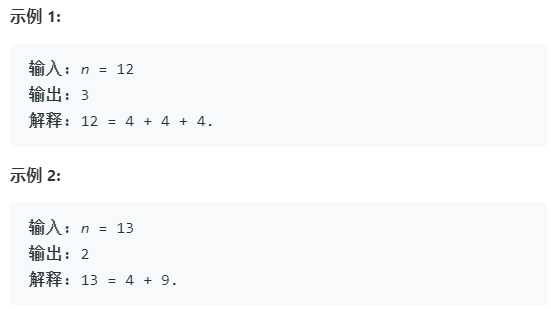
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
初始思路: 给定一个数比如1300,1300下一步分解就有 int( 1300**(0.5) +1) 种选择,再下一步又有很多种选择,这样自顶向下的分解方法无疑是不可行的。
dp思路,从底向上推,从1-1300 每一步的最小步数都存在dp中,这样可以避免很多重复计算。
dp = [ for i in range( n + 1) ]
代码:
class Solution:
def numSquares(self, n: int) -> int:
dp = [i for i in range(n+1)]
for i in range(2,n+1):
for j in range(1,int(i**(0.5))+1):
dp[i] = min(dp[i],dp[i - j*j]+1)
return dp[-1]
本题的技巧:
1. 如果 i - j*j == 0: 刚好访问到 dp[ 0 ],则刚好本步为 dp[ 0 ] + 1 = 1
2. 遍历n下的所有平方数,之后的哪个dp[ n - j*j ]大就取谁。
279.完全平方数(动态规划)
原文:https://www.cnblogs.com/ChevisZhang/p/12352985.html
