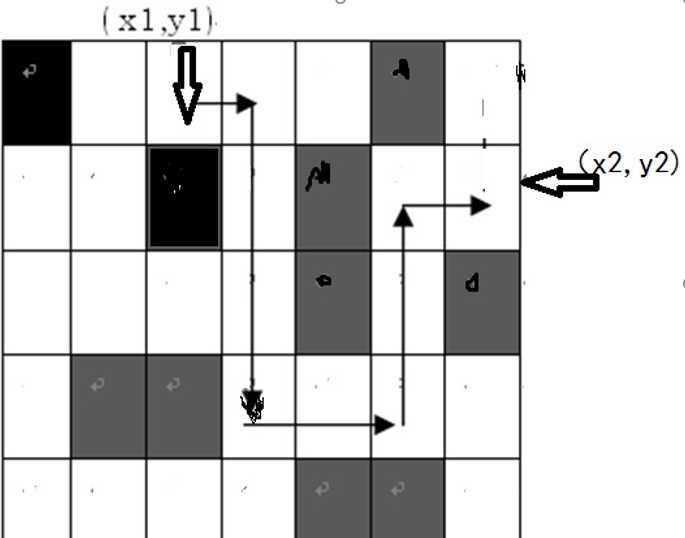
给出一张地图,这张地图被分为n×m(n,m<=100)个方块,任何一个方块不是平地就是高山。平地可以通过,高山则不能。现在你处在地图的(x1,y1)这块平地,问:你至少需要拐几个弯才能到达目的地(x2,y2)?你只能沿着水平和垂直方向的平地上行进,拐弯次数就等于行进方向的改变(从水平到垂直或从垂直到水平)的次数。例如:如图,最少的拐弯次数为5。
输入格式
第1行:n m
第2至n+1行:整个地图地形描述(0:空地;1:高山),
如(图)第2行地形描述为:1 0 0 0 0 1 0
第3行地形描述为:0 0 1 0 1 0 0
第n+2行:x1 y1 x2 y2 (分别为起点、终点坐标)
输出格式
s (即最少的拐弯次数)
样例输入
5 7
1 0 0 0 0 1 0
0 0 1 0 1 0 0
0 0 0 0 1 0 1
0 1 1 0 0 0 0
0 0 0 0 1 1 0
1 3 1 7
样例输入
5
import java.util.ArrayList; import java.util.Scanner; public class test { //王耀辉 static Scanner sc=new Scanner(System.in); //n为长 m为宽 a为地图信息 b为记录点是否走过 l为记录走的点得坐标 min找的得最小值 fang为方向数组 static int n=sc.nextInt(); static int m=sc.nextInt(); static int [][]a=new int[n][m]; static boolean [][]b=new boolean[n][m]; static ArrayList<Integer> l=new ArrayList<Integer>(); static int []fang={-1,0,1,0,0,-1,0,1}; static int min=Integer.MAX_VALUE; public static void main(String[] args) { //存入地图信息 for (int i = 0; i <n; i++) { for (int j = 0; j < m; j++) { a[i][j]=sc.nextInt(); } } //x1,y1起点坐标 x2,y2终点坐标 int x1=sc.nextInt()-1; int y1=sc.nextInt()-1; int x2=sc.nextInt()-1; int y2=sc.nextInt()-1; l.add(x1); l.add(y1); b[x1][y1]=true; f(x1,y1,x2,y2); System.out.println(min); } private static void f(int x1, int y1, int x2, int y2) { // TODO Auto-generated method stub if (x1==x2&&y1==y2) { //存我现在走得方向 int []fang1=new int[2]; //记录我转了几次 int ji=0; //循环我的路线集合 for (int i = 2; i <l.size()-2; i+=2) { //判断我这步走的方向是否和下一步走的一样 if (l.get(i)+fang1[0]==l.get(i+2)&&l.get(i+1)+fang1[1]==l.get(i+3)) { continue; }else { //更改方向 fang1[0]=l.get(i+2)-l.get(i); fang1[1]=l.get(i+3)-l.get(i+1); ji++; } } //找到最小值 if (ji<min) { min=ji; } }else { for (int i = 0; i < fang.length; i+=2) { //接下来要走得坐标 int x=x1+fang[i]; int y=y1+fang[i+1]; //判断接下来是否越界 和 接下来是否走过 接下来走的是否是平原 if (x>=0&&x<n&&y>=0&&y<m&&!b[x][y]&&a[x][y]==0) { x1+=fang[i]; y1+=fang[i+1]; b[x1][y1]=true; l.add(x1); l.add(y1); f(x1,y1,x2,y2); b[x1][y1]=false; x1-=fang[i]; y1-=fang[i+1]; l.remove(l.size()-1); l.remove(l.size()-1); } } } } }
原文:https://www.cnblogs.com/shiaguang/p/12357547.html