Min-Max容斥学习笔记

越学了Min-Max容斥 ， 越发察觉到自己的弱小。。。
对于一个集合S ， 设S中最大的元素为max(S) , 最小的是min(S)
那么Min-Max容斥的结论是

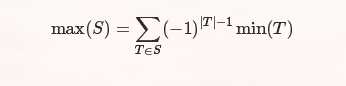
这个Min-Max容斥一般用于集合内的元素没有办法比较大小时。
对于期望也成立。

简略证明一下正确性
（其实就是搬运题解）
设S中的最大值是maxval
若一个集合中的最小值是maxval ， 那这个集合一定是 { maxval } , 也就是maxval这个元素组成的集合。
这个时候系数是1 ， 没毛病。
之后对于一个元素x ， 他是第k大 k < n 那么他作为min出现了\(2^{n-k}\) 次 ， 这其中有一半集合大小为偶数 ， 另一半集合大小为奇数 。 这样一抵消 ， 就把x消去了。

一道例题

• P3175 [HAOI2015]按位或

在这个题里 ， max(S) 就是所有位上都是1 ， min(S) 就是S集合中有一位是1的最早的。
集合里的元素就是各个位置变成1的期望步数，这个东西显然没法比较大小。
由于Min-Max容斥对于期望也成立 。 那么现在问题就变成了怎么求min（S）；

考虑总的集合为U ， 那么P(min(S) == k)是啥。
P是概率。
会有前k-1次选择的是 U ^ S 中的元素 ， 且在第K次选了S中的元素。
\(P(min(S) == k) = P(U xor S) ^{k-1} * (1 - P(U xor S))\)

有一个玩意叫 离散随机变量的几何分布

先说啥叫离散随机变量

离散随机变量就是一个随机变量只可以取一些特定的不连续值，比如全体正整数之类的……

那么我们描述一个离散随机变量的最朴素的方式就是列一个表……，打出每个值的概率，然后就可以描述一个离散随机变量的分布了

那么所谓的集合分布呢，就是这里有一个离散型随机变量X,满足
\(P(x == k) = (1 - p) ^ {k-1} * p\)

其中p是一个常量

那他的期望呢

\(E(x) = \sum_{i=0}^inf P(x == i)\)
$ = \sum_{i=0}^inf (1-p)^(i-1) * p = p * \sum_{i=0}^inf (1-p)^(i-1) = 1 / p$

然后再看\(P(min(S) == k) = P(U xor S) ^{k-1} * (1 - P(U xor S))\)
发现这个式子是满足p = (1 - P(U xor S)) 的离散型随机变量的集合分布。

那么最后一个问题 P(U^S) 怎么求。
P(x) = P(x所有子集)
这个东西用FWT解决即可。

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
const double eps = 1e-8;
inline int read()
{
    register int x = 0 , f = 0; register char c = getchar();
    while(c < '0' || c > '9') f |= c == '-' , c = getchar();
    while(c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0' , c = getchar();
    return f ? -x : x;
}
int n;
int siz[1<<21];
double a[1<<21];
int main()
{
    n = read(); int lim = 1 << n;
    for(int i = 0 ; i < lim ; ++i) scanf("%lf" , &a[i]);
    for(int mid = 1 ; mid < lim ; mid <<= 1)
        for(int j = 0 ; j < lim ; j += mid << 1)
            for(int k = 0 ; k < mid ; ++k)
                a[j + k + mid] += a[j + k];
    for(int i = 1 ; i < lim ; ++i) siz[i] = siz[i >> 1] + (i & 1);
    #define stop { puts("INF"); return 0; }
    double ans = 0;
    for(int i = 1 ; i < lim ; ++i)
    {
        double k = 1.0 - a[(lim - 1) ^ i];
        if(k < eps) stop; k = 1.0 / k;
        if(siz[i] & 1) ans += k; else ans -= k;
    }
    printf("%.10f\n" , ans);
    return 0;
}

Min-Max容斥学习笔记

原文：https://www.cnblogs.com/R-Q-R-Q/p/12358279.html