分析思维 第四篇：数据分析入门阶段——描述性统计分析和相关分析

数据分析的入门思维，首先要认识数据，然后对数据进行简单的分析，比如描述性统计分析和相关性分析等。

一，认识变量和数据

变量和数据是数据分析中常用的概念，用变量来描述事物的特征，而数据是变量的具体值，把变量的值也叫做观测值。

1，变量

变量是用来描述总体中成员的某一个特性，例如，性别、年龄、身高、收入等。

变量可以分为：

• 定性变量：用于分类，一般是文本，例如，性别、颜色
• 定序变量：用于表示等级或次序的变量，例如，学历，职位，排名等，变量的值可以把事务排列为高低或大小，但是各个变量值之间没有确切的间隔距离，无法确定两个定序变量之间相差多少。
• 定量变量：是数量变量，能够比较大小。分为两类：离散变量和连续变量。

2，数据

数据是变量的具体值，按照变量的类型，可以把数据分为：分类数据、顺序数据和数值型数据。

按照数据分析的目的，可以把数据分为实验组（Treatment）和参照组（Control）。

按照数据的类型，可以把数据分为：文本数据、数值型数据和日期时间数据。

3，缺失值

不是所有的数据都是完整的，有些观测值可能会缺失，对于缺失值，通常的处理方式是：删除缺失值所在的数据行，填充缺失值、插补缺失值。

4，观测值的重编码

数据分析中，通常需要把连续型变量转换为定序变量，例如，把学生的成绩划分为优秀、良好、合格和差4个等级，这种操作也称作离散化。

当观测数据所用的单位可能影响数据分析时，还需要对数据进行规范化，常用的规范化方法是：最小-最大规范化，标准化变换等。

观测值的重编码，后续会有详细的介绍。

二，描述性统计分析

描述性统计量分为：集中趋势、离散程度（离中趋势）和分布形态。

1，集中趋势的描述性统计量

• 均值：是指一组数据的算术平均数，描述一组数据的平均水平，是集中趋势中波动最小、最可靠的指标，但是均值容易受到极端值（极小值或极大值）的影响。
• 中位数：是指当一组数据按照顺序排列后，位于中间位置的数，不受极端值的影响，对于定序型变量，中位数是最适合的表征集中趋势的指标。
• 众数：是指一组数据中出现次数最多的观测值，不受极端值的影响，常用于描述定性数据的集中趋势。

2，离散程度的描述性统计量

• 最大值和最小值：是一组数据中的最大观测值和最小观测值
• 极差：又称全距，是一组数据中的最大观测值和最小观测值之差，记作R，一般情况下，极差越大，离散程度越大，其值容易受到极端值的影响。
• 方差和标准差：是描述一组数据离散程度的最常用、最适用的指标，值越大，表明数据的离散程度越大。

3，分布形态的描述性统计量

偏度：用来评估一组数据的分布呈先的对称程度，当偏度=0时，分布是对称的；当偏度>0时，分布呈正偏态；当偏度<0时，分布呈负偏态。

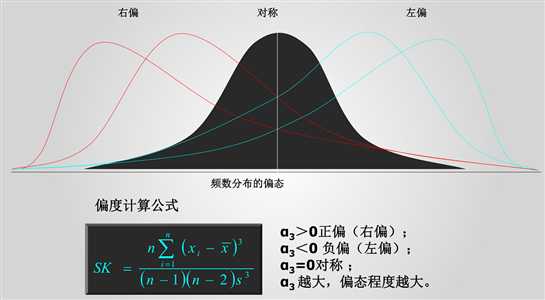
峰度：用来评估一组数据的分布形状的高低程度的指标，当峰度=0时，分布和正态分布基本一直；当峰度>0时，分布形态高狭；当峰度<0时，分布形态低阔。

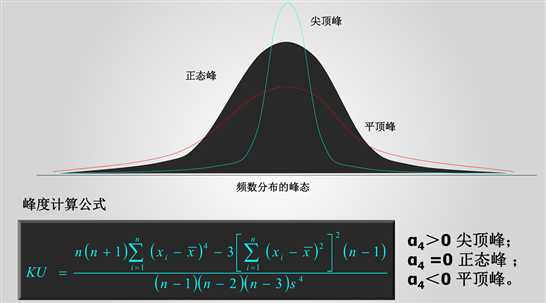
4，频率分析

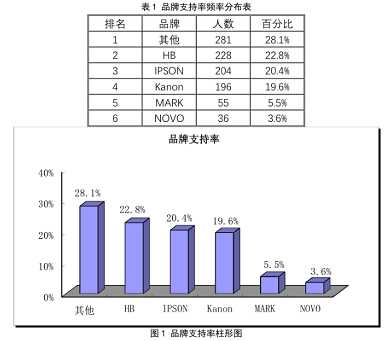
频数分布分析（又称频率分析）主要通过频数分布表、条形图和直方图、百分位值等来描述数据的分布特征。

在做频数分布分析时，通常按照定性数据（即分类的类别），统计各个分类的频数，计算各个分类所占的百分比，进而得到频率分布表，最后根据频率分布表来绘制频率分布图。

5，按照时间递增的趋势分析

特殊情况下，当X轴是日期数据，Y轴是统计量（比如均值、总数量）时，可以绘制出统计量按照时间递增的趋势图，从图中可以看到统计量按照时间增加的趋势（无变化、递增或递减）和周期性。

例如，下图的X轴是日期，Y轴的统计量是总数量，两条折线分别是湖北确诊病例人数和湖北新增确诊病例人数：

三，相关性分析 

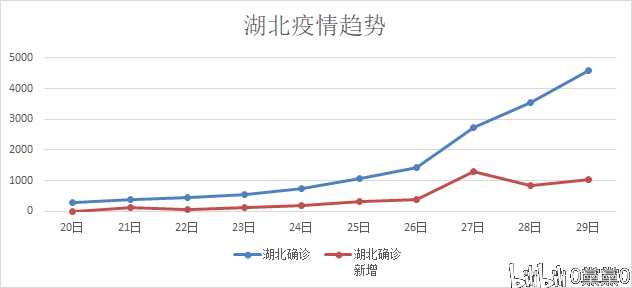
相关性分析是研究事务之间是否存在某种依存关系，并对具有依存关系的现象进行相关方向和相关程度的分析。

相关程度用相关系数r表示，|r|<=1，r=0表示不相关，通常情况下，0 < | r | <1表示变量之间存在不同程度的线性相关，根据约定的规则：

• | r | <=0.3 ：为弱线性相关或不存在线性相关；
• 0.3 < | r | <=0.5 ：低度线性相关，认为存在线性相关，但是相关性不明显
• 0.5 < | r | <=0.8 ：显著线性相关，认为存在强线性相关，存在明显的相关性
• | r | >0.8 ：高度相关，认为存在极强的线性相关

参考文档：

分析思维 第四篇：数据分析入门阶段——描述性统计分析和相关分析

原文：https://www.cnblogs.com/ljhdo/p/11501415.html