Harris角点检测算法

• 1.利用水平，竖直差分算子对图像的每个像素进行滤波以求得Ix,Iy,进而求得M中的四个元素的值。
  
  
  

  代码中如果窗口数组array为-1,0,1,-1,0,1,-1,0,1}则是求解X方向的，如果为{-1,-1,-1,0,0,0,1,1,1}为Y方向的，则Ix和Iy求解结束，求解IX2相对比较简单，像素相乘即可。

• 2.对M的四个元素进行高斯平滑滤波，为的是消除一些不必要的孤立点和凸起，得到新的矩阵M。
• 3.3.接下来利用M计算对应每个像素的角点响应函数R，即：
  
• 4、局部极大值抑制，同时选取其极大值
• 5.在矩阵R中，同时满足R(i,j)大于一定阈值threshold和R(i,j)是某领域内的局部极大值，则被认为是角点

三，代码

 1 from pylab import *
 2 from PIL import Image
 3 from PCV.localdescriptors import harris
 4 """
 5 Example of detecting Harris corner points (Figure 2-1 in the book).
 6 """
 7 # 读入图像
 8 im = array(Image.open(r‘b3.jpg‘).convert(‘L‘))
 9 # 检测harris角点
10 harrisim = harris.compute_harris_response(im)
11 # Harris响应函数
12 harrisim1 = 255 - harrisim
13 figure()
14 gray()
15 #画出Harris响应图
16 subplot(141)
17 imshow(harrisim1)
18 print (harrisim1.shape)
19 axis(‘off‘)
20 axis(‘equal‘)
21 threshold = [0.01, 0.05, 0.1]
22 for i, thres in enumerate(threshold):
23     filtered_coords = harris.get_harris_points(harrisim, 6, thres)
24     subplot(1, 4, i+2)
25     imshow(im)
26     print (im.shape)
27     plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], ‘*‘)
28     axis(‘off‘)
29 show()

四，运行结果

　4.1纹理平坦的图

　　　4.1.1正面

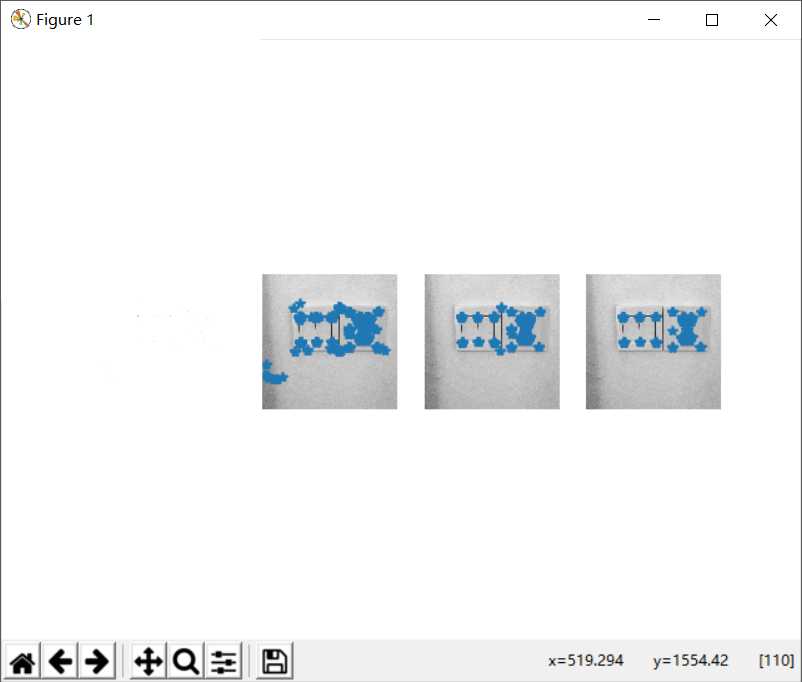
　　　4.1.2侧面

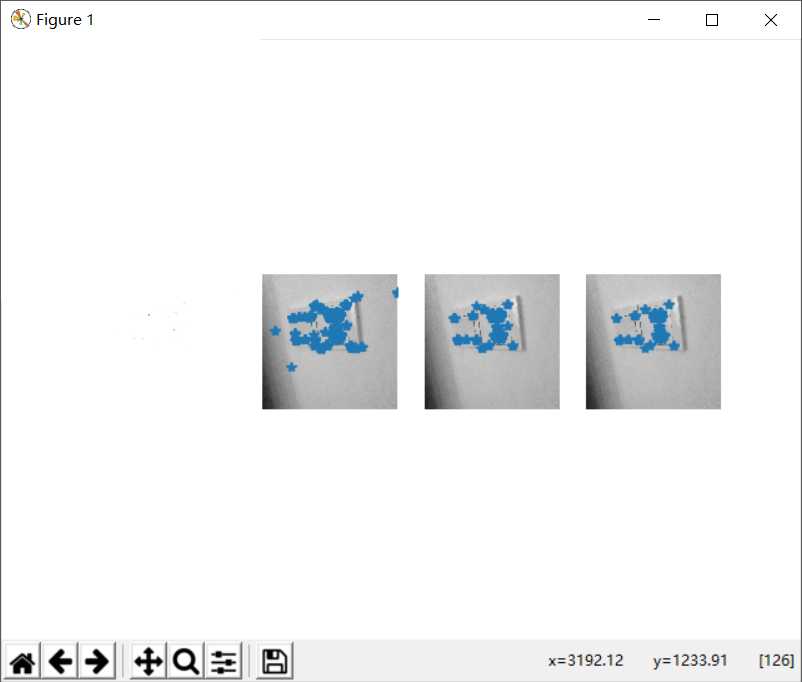
　　　4.1.3旋转

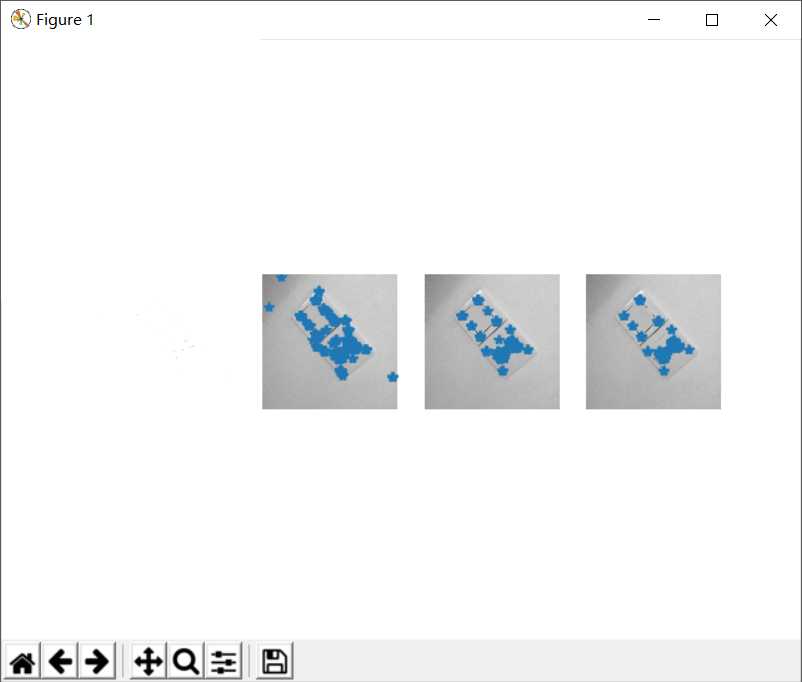
　　　4.1.4相对较远处

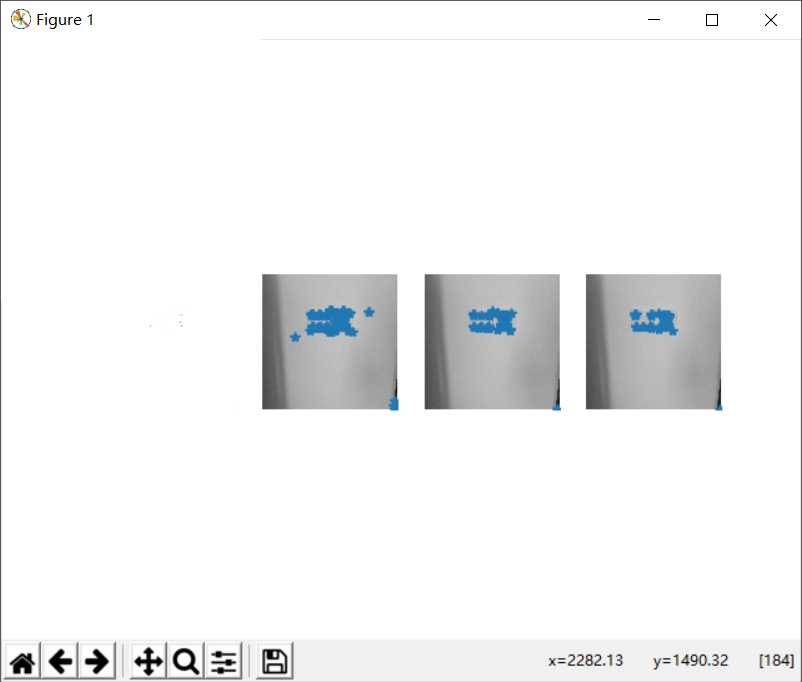
　　　 4.1.5较亮情况

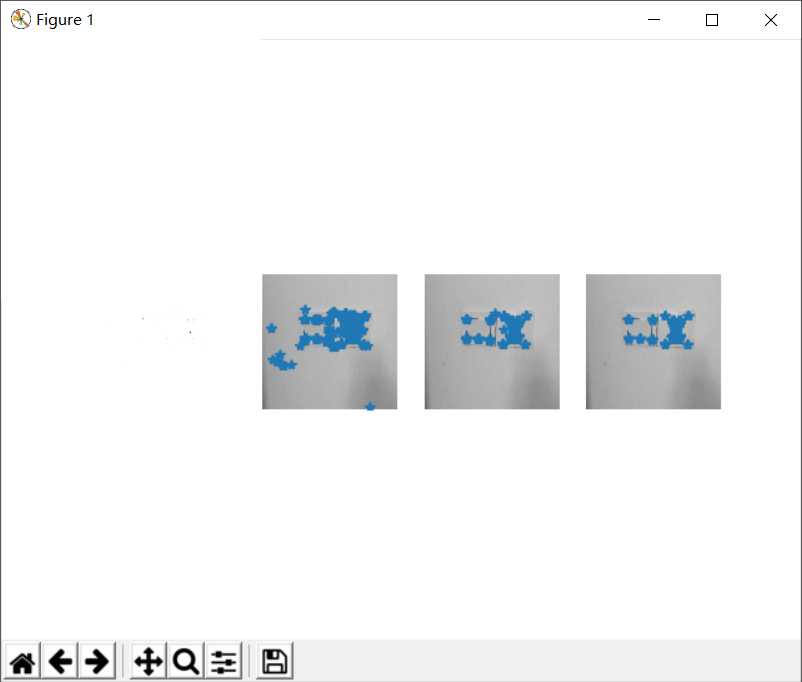
　4.2垂直或水平边缘多

　　  4.2.1正面

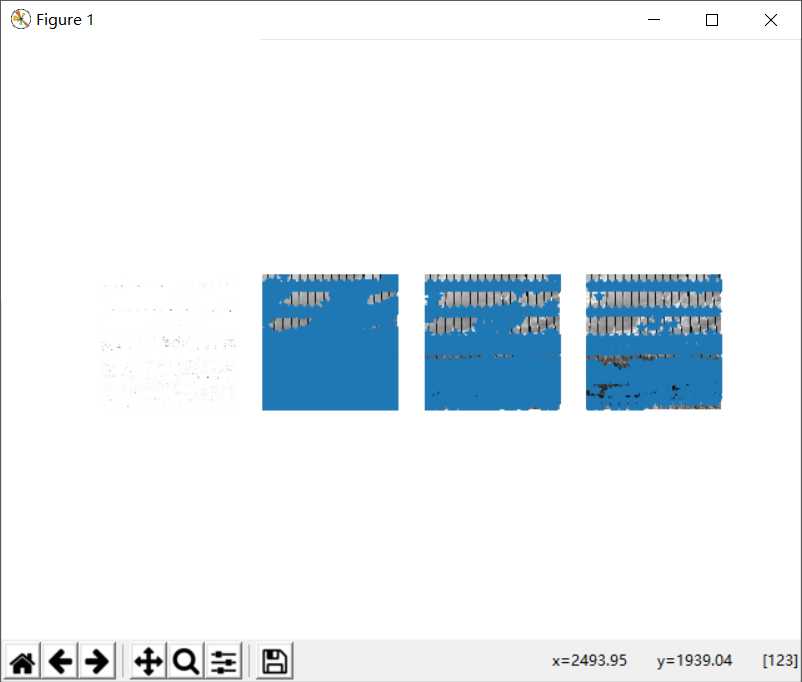
　　　 4.2.2侧面

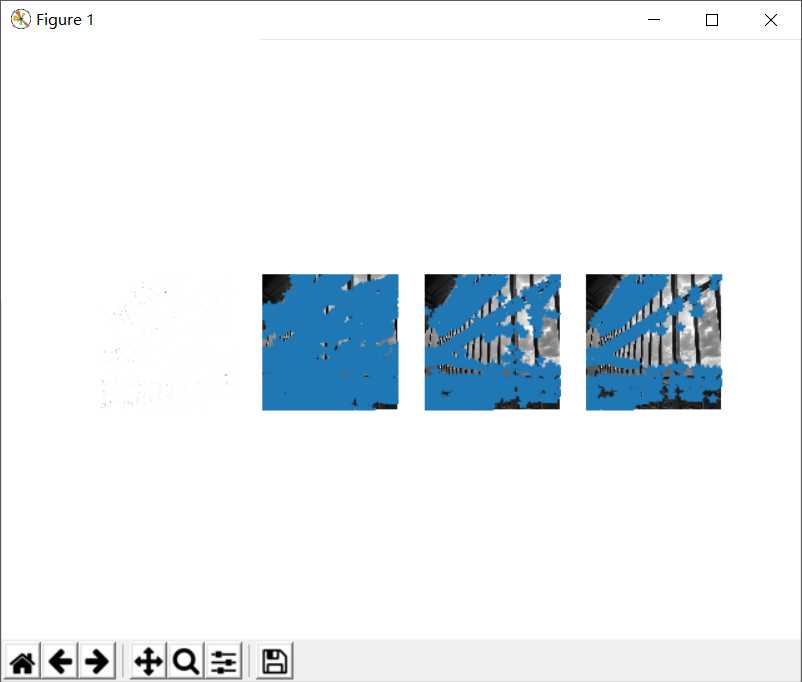
　　　4.2.3旋转

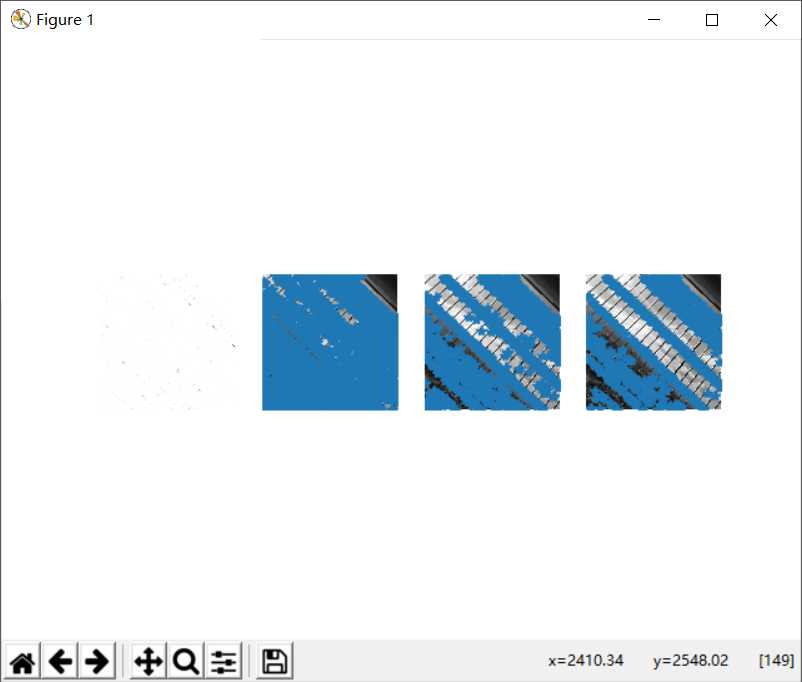
　　　　4.2.4相对较远处

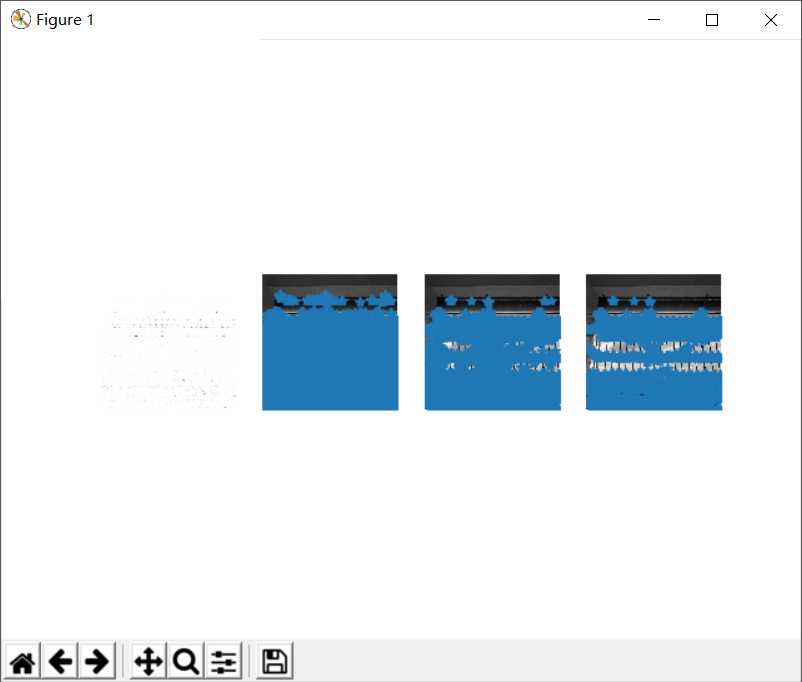
　4.3纹理角点丰富

　　   4.3.1正面

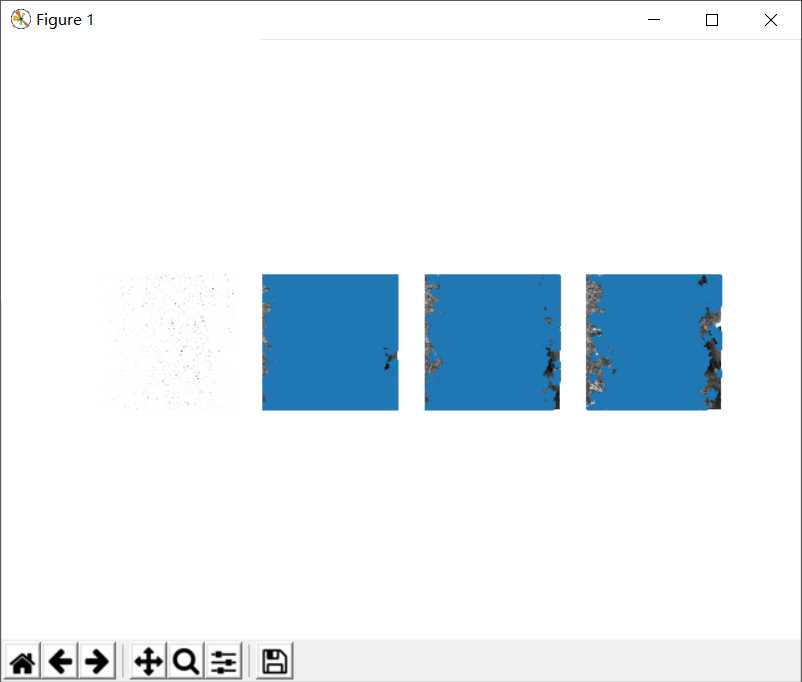
　　　  4.3.2侧面

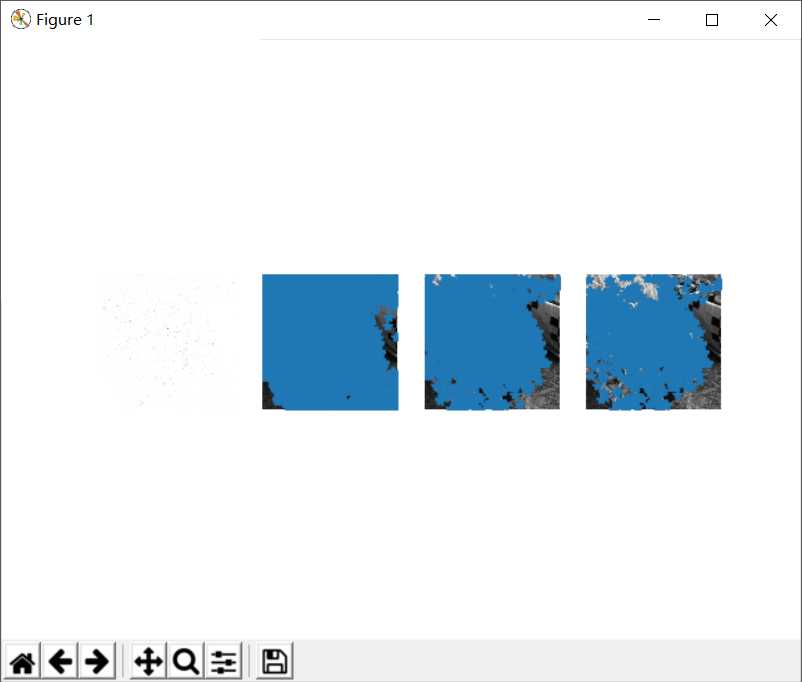
　　　4.3.3旋转

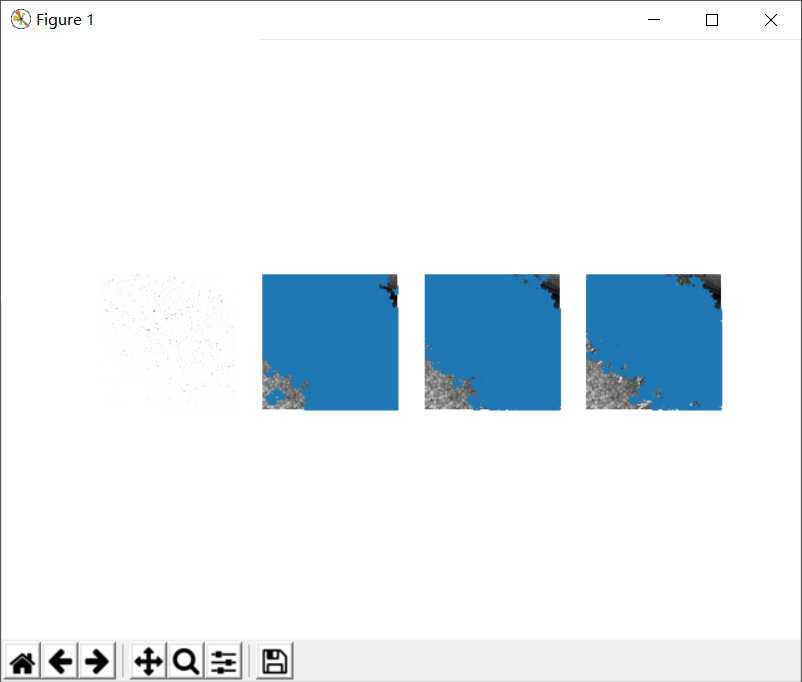
　　　4.3.4相对较远处

五，结论以及实验中遇到的问题

　5.1实验结果分析

1. Harris角点具有旋转不变性。

Harris角点检测通过窗口对应的二阶矩阵M 的特征值得到角点响应值R，从而判断角点。当图像转动时，角点区域的像素点梯度坐标和拟合椭圆对应地发生旋转，但是矩阵的特征值（也可以理解为数据点区域的拟合椭圆）不变，因此图像旋转不影响角点的检测。

2. Harris角点检测算子对亮度和对比度的变化不灵敏
　　这是因为在进行Harris角点检测时，使用了微分算子对图像进行微分运算，而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。换言之，对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置，但是，阈值的选择可能会影响角点检测的结果。

3. Harris角点检测算子不具有尺度不变性

当图像被缩小或放大时，在检测窗口尺寸不变的前提下，在窗口内所包含图像的内容是完全不同的，角点检测的性能也会发生改变。

　5.2实验中遇到的问题

　　PCV，是一个很老的包了，从下载地址：https://github.com/jesolem/PCV (原链接，适用于python2），但在python3的时代里已不适用。需要将原文件里的多个print语句改写成python3的形式才能正常安装。