C++ 全排列问题——递减进位法

求一个全排列的下m个全排列，我们发现递增进位法每次进位的次数太多，因此为了对其进行优化出现了递减进位法。

例题

原创例题

题目描述
求排列a[1]，a[2]，a[3]，……，a[n]之后按递减进位法的第m个全排列。

输入格式
共三行。
第一行一个正整数N（1 <= N <= 10000）。
第二行一个正整数M（1 <= N <= 100）。
下一行是1到N这N个整数的一个排列，用空格隔开。

输出格式
N个整数，表示按递减进位法第m个全排列。每两个相邻的数中间用一个空格分开。（这里不是字典序）

输入输出样例
输入

5
3
1 2 3 4 5

输出

1 5 2 3 4

全排列问题——递减进位法

这里对于一个全排列我们需要一个中介数，举个例子假设我们要求839647521按递增进位法的下100个全排列，这里我们生成其对应的中介数：1后面比1小的有0个数，2后面比2小的有1个数，3后面比3小的有2个数，4后面比4小的有2个数……mid[i]表示i后面比i小的数的个数，这里把i换成a[i]，经过整理i = a[i]，mid[a[i]]可以表示a[i]后面比a[i]小的数的个数，得到中介数mid = 012224376。

我们可以发现对于mid[i]最大为(i - 1)，因为比i小的数只有(i - 1)个。这样我们就可以发现中介数mid除去第一个0就是一个递增进位制数（第i位的进位制是i，首位是二进制，因为一进制恒为0），这样我们让这个递减进位制数12224376加上100，就是12224527。

递减进位制(12224376) + 十进制(100)

• 倒数第一位是6 + 100 = 106，进位制是9，所以向下一位进11，mid[n] = 7。
• 倒数第二位是7 + 11 = 18，进位制是8，所以向下一位进2，mid[n - 1] = 2。
• 倒数第三位是3 + 2 = 5，进位制是7，所以不再进位，mid[n - 2] = 5。

最后得到递减进位制(12224527)，这也就是下100个排列的中介数了。这里我们就发现递减进位法的进位次数就比递增进位法的进位次数少了许多。

这里要加个特判：如果mid[1]大于0了，代表这个排列比排列n，(n - 1)，……，1还大，那么根本没有这种排列，所以直接返回false就行了。

用递减进位制数再求出排列：中介数mid[i]表示i后面比i小的数的个数，因此我们每次从第n个位置倒着数(mid[i] + 1)个空位，这里选过的位置不能再算在其中，最后再把i放到数到的这个位置上就完成了一个i（i要从n到1倒着进行枚举），下面是例子。

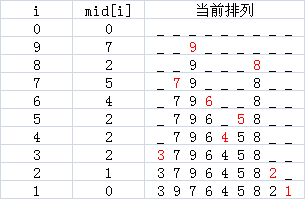
最后算一下算法时间复杂度：最多的有两重循环，所以时间复杂度是O(n^2^)。

代码

# include <cstdio>
# include <cmath>
# include <cstring>
# include <algorithm>

using namespace std;

const int N_MAX = 10000;

int n, m = 1;
int a[N_MAX + 10];
int mid[N_MAX + 10]; // mid[i]表示排列中i这个数后面比i小的数的个数
bool flag[N_MAX + 10]; // flag[i]表示新排列中位置i是否被占用 

bool permutation()
{
    memset(mid, 0, sizeof(mid));
    memset(flag, 0, sizeof(flag));
    for (int i = 1; i <= n - 1; i++)
        for (int j = i + 1; j <= n; j++)
            mid[a[i]] += (a[i] > a[j]);
    mid[n] += m;
    for (int i = n; i >= 2 && mid[i] >= i; i--) {
        mid[i - 1] += mid[i] / i;
        mid[i] %= i;
    }
    if (mid[1] > 0) return false;
    for (int i = n; i >= 1; i--) {
        int pos = n;
        for (int j = 0; pos >= 1; pos--) {
            j += !flag[pos];
            if (j > mid[i]) break;
        }
        flag[pos] = true;
        a[pos] = i;
    }
    return true;
}

int main()
{
    scanf("%d", &n);
    scanf("%d", &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    permutation();
    for (int i = 1; i <= n; i++)
        printf("%d ", a[i]);
    printf("\n");
    return 0;
}

C++ 全排列问题——递减进位法

原文：https://www.cnblogs.com/000zwx000/p/12365145.html