C++ 全排列问题——递增进位法

求一个全排列的下m个全排列，有时我们并不想按字典序找，而是想换一种顺序去找。

例题

原创例题

题目描述
求排列a[1]，a[2]，a[3]，……，a[n]之后按递增进位法的第m个全排列。

输入格式
共三行。
第一行一个正整数N（1 <= N <= 10000）。
第二行一个正整数M（1 <= N <= 100）。
下一行是1到N这N个整数的一个排列，用空格隔开。

输出格式
N个整数，表示按递增进位法第m个全排列。每两个相邻的数中间用一个空格分开。（这里不是字典序）

输入输出样例
输入

5
3
1 2 3 4 5

输出

2 3 1 4 5

全排列问题——递增进位法

这里对于一个全排列我们需要一个中介数，举个例子假设我们要求839647521按递增进位法的下100个全排列，这里我们生成其对应的中介数：9后面比9小的有6个数，8后面比8小的有7个数，7后面比7小的有3个数，6后面比6小的有4个数……mid[i]表示(n - i + 1)后面比(n - i + 1)小的数的个数，这里把(n - i + 1)换成a[i]，经过整理i = n - a[i] + 1，mid[n - a[i] + 1]可以表示a[i]后面比a[i]小的数的个数，得到中介数mid = 673422210。

我们可以发现对于mid[i]最大为(n - i)，因为比(n - i + 1)小的数只有(n - i)个。这样我们就可以发现中介数mid除去最后一个0就是一个递增进位制数（第i位的进位制是(n - i + 1)，最后一位是二进制，因为一进制恒为0），这样我们让这个递增进位制数67342221加上100，就是67351311。

递增进位制(67342221) + 十进制(100)

• 倒数第一位是1 + 100 = 101，进位制是2，所以向下一位进50，mid[n - 1] = 1。
• 倒数第二位是2 + 50 = 52，进位制是3，所以向下一位进17，mid[n - 2] = 1。
• 倒数第三位是2 + 17 = 19，进位制是4，所以向下一位进4，mid[n - 3] = 3。
• 倒数第四位是2 + 4 = 6，进位制是5，所以向下一位进1，mid[n - 4] = 1。
• 倒数第五位是4 + 1 = 5，进位制是6，所以不再进位，mid[n - 5] = 5。

最后得到递增进位制(67351311)，这也就是下100个排列的中介数了。

这里要加个特判：如果mid[0]大于0了，代表这个排列比排列n，(n - 1)，……，1还大，那么根本没有这种排列，所以直接返回false就行了。

用递增进位制数再求出排列：中介数mid[i]表示(n - i + 1)后面比(n - i + 1)小的数的个数，因此我们每次从第n个位置倒着数(mid[i] + 1)个空位，这里选过的位置不能再算在其中，最后再把(n - i + 1)放到数到的这个位置上就完成了一个i，下面是例子。

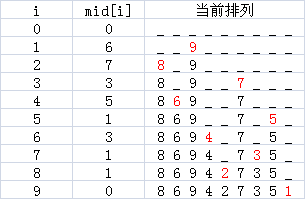
最后算一下算法时间复杂度：最多的有两重循环，所以时间复杂度是O(n^2^)。

代码

# include <cstdio>
# include <cmath>
# include <cstring>
# include <algorithm>

using namespace std;

const int N_MAX = 10000;

int n, m;
int a[N_MAX + 10];
int mid[N_MAX + 10]; // mid[i]表示排列中(n - i + 1)这个数后面比(n - i + 1)小的数的个数
bool flag[N_MAX + 10]; // flag[i]表示新排列中位置i是否被占用 

bool permutation()
{
    memset(mid, 0, sizeof(mid));
    memset(flag, 0, sizeof(flag));
    for (int i = 1; i <= n - 1; i++)
        for (int j = i + 1; j <= n; j++)
            mid[n - a[i] + 1] += (a[i] > a[j]);
    mid[n - 1] += m;
    for (int i = n - 1; i >= 1 && mid[i] >= n - i + 1; i--) {
        mid[i - 1] += mid[i] / (n - i + 1);
        mid[i] %= n - i + 1;
    }
    if (mid[0] > 0) return false;
    for (int i = 1; i <= n; i++) {
        int pos = n;
        for (int j = 0; pos >= 1; pos--) {
            j += !flag[pos];
            if (j > mid[i]) break;
        }
        flag[pos] = true;
        a[pos] = n - i + 1;
    }
    return true;
}

int main()
{
    scanf("%d", &n);
    scanf("%d", &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    permutation();
    for (int i = 1; i <= n; i++)
        printf("%d ", a[i]);
    printf("\n");
    return 0;
}

C++ 全排列问题——递增进位法

原文：https://www.cnblogs.com/000zwx000/p/12365074.html