牛顿迭代法主要解决的是方程近似求根问题,关于牛顿迭代法的详细推导和数学原理见此链接;
https://www.matongxue.com/madocs/205.html
https://oi-wiki.org/math/newton/
接下来主要说一下怎么利用牛顿迭代法进行求根,其实就是利用这种迭代计算思想来借助递推公式进行求解;
对于一个数n来说,如果相求他的二次方根,本质上就是使得x^2=n,求出x即可;
假若对于一个一般性的方程y=x^2-n,如果求他的根,也就是当y=0时,x为何值,对于代数解法,有:
y=0=x^2-n得到x^2=n,所以解出的x即为所需要的根;
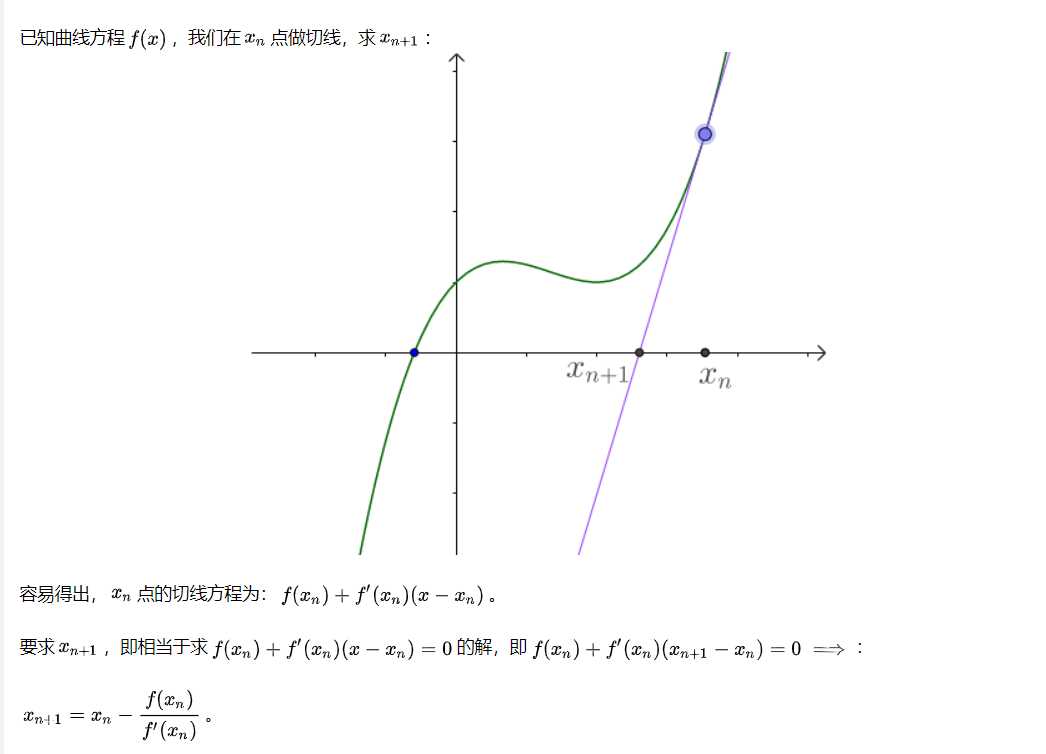
所以如果按照这个递推公式推导,则有:
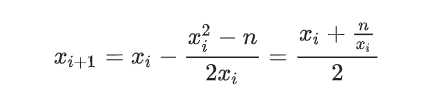
所以本质上就是一直按照这个递推公式进行求导;
如果设置误差eps,则时每次第i个x和第i+1个x相减小于误差eps;
#include<iostream> #include<fstream> #include<sstream> #include<vector> #include<string> #include<cstring> #include<algorithm> #include<math.h> using namespace std; double newsqrt(double n,double eps) { double x = 1; while (1) { double nx = (x + n / x) / 2; if (abs(nx - x) < eps) return nx; x = nx; } } int main(){ int n; double e = 1e-10; cin >> n; printf("%lf\n", newsqrt(double(n), e)); return 0; }
原文:https://www.cnblogs.com/songlinxuan/p/12368395.html