链接:https://leetcode-cn.com/problems/combination-sum/
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
由于可以无限制选取,所以我们如果选了一次某数字之后,我们还可以再次选择这个数。
注意题目说了无重复元素。所以只要我们按顺序找,并且不选取之前已经放弃的元素,我们最终的解就不会重复。
比如:1,3,2,Target=6。我们第一层遍历时选取了1,然后一定会得到一个1+3+2=6的解。之后我们不选择1,从3开始寻找新的解。除了得到3+3=6之外,我们不能再选取1,因为我们选取1的情况已经在之前考虑过了。
避免重复选取元素的方法有两个:
1 class Solution { 2 public: 3 vector<vector<int>> res; 4 vector<int> cur; 5 vector<vector<int>> combinationSum(vector<int>& candidates, int target) { 6 dfs(0,target,candidates); 7 return res; 8 } 9 void dfs(int idx,int to_go,vector<int>& nums){ 10 //从idx开始继续选取可能的元素,to_go是距离目标值的差值 11 if(to_go==0){ 12 res.emplace_back(cur); 13 return; 14 } 15 if(idx>=nums.size()){ 16 return; 17 } 18 for(int i=idx;i<nums.size();++i){ 19 if(nums[i]<=to_go){ 20 cur.emplace_back(nums[i]); 21 dfs(i,to_go-nums[i],nums);//注意这里选取i之后,递归的dfs又继续从i开始选取 22 cur.pop_back(); 23 } 24 } 25 } 26 };
由于本题没有重复元素,所以如果我们的每个解的组成数字都是严格递增or递减的,我们也不会求出重复解。那么这种做法要求我们先对数组排序。(虽然其实排好序按元素递增顺序遍历,也是相当于按照数组索引顺序遍历,但毕竟一开始的出发点是不一样的。)
1 class Solution { 2 public: 3 vector<vector<int>> res; 4 vector<int> cur; 5 vector<vector<int>> combinationSum(vector<int>& candidates, int target) { 6 sort(candidates.begin(),candidates.end()); 7 dfs(0,target,candidates); 8 return res; 9 } 10 void dfs(int idx,int to_go,vector<int>& nums){ 11 //从idx开始继续选取可能的元素,to_go是距离目标值的差值 12 if(to_go==0){ 13 res.emplace_back(cur); 14 return; 15 } 16 if(idx>=nums.size()){ 17 return; 18 } 19 for(int i=idx;i<nums.size();++i){ 20 if(nums[i]<=to_go){ 21 cur.emplace_back(nums[i]); 22 dfs(i,to_go-nums[i],nums);//注意这里选取i之后,递归的dfs又继续从i开始选取 23 cur.pop_back(); 24 } 25 } 26 } 27 };
链接:https://leetcode-cn.com/problems/combination-sum-ii/
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
首先该数组没说无重复,那么就意味着会有重复元素。比如1,2,1,Target=3这种例子,我们只能求出一组(1,2)的解,不能求出(1,2)和(2,1)两组解,因为这是重复解。
另外该数组每个数字只能使用一次,即我们选取了某个数字i,则之后的遍历中都不能选择i了。
所以我们代码需要在前一题的基础上做一些修改。
首先是for循环中递归dfs的时候,需要把下次选取的起始索引从i改为i+1,因为在每个数字只能使用一次的前提下,我们既然选取了i就不能再次选取i了。
即:
1 dfs(i+1,to_go-nums[i],nums);//注意这里选取i之后,递归的dfs从i+1开始选取
如果我们只改动这一句,运行一下我们的代码:
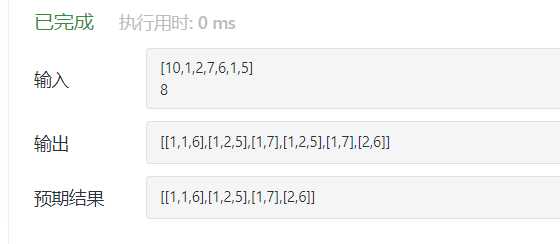
发现会算出重复的解。不难理解,这是由于原数组有重复的元素,而我们的算法没有考虑重复的元素出现。
那么如何去重?有两个方法:
1.暴力。全部解算完之后,对每个解内部排序,放入集合去重,但这样显然不是很好的方法。
2.我们可以举栗子看下为什么算出重复的解:用上面图片的栗子,我们的解出现了两个[1,2,5],原因是先取了第一个1和后面的2,5,它们组成了一个解。之后不取第一个1继续往后遍历。直到选取了2,5和第二个1,这样又构成了一组解。所以看来问题是同样的元素如果分散在数组两侧,我们就可能会算出一样的解。
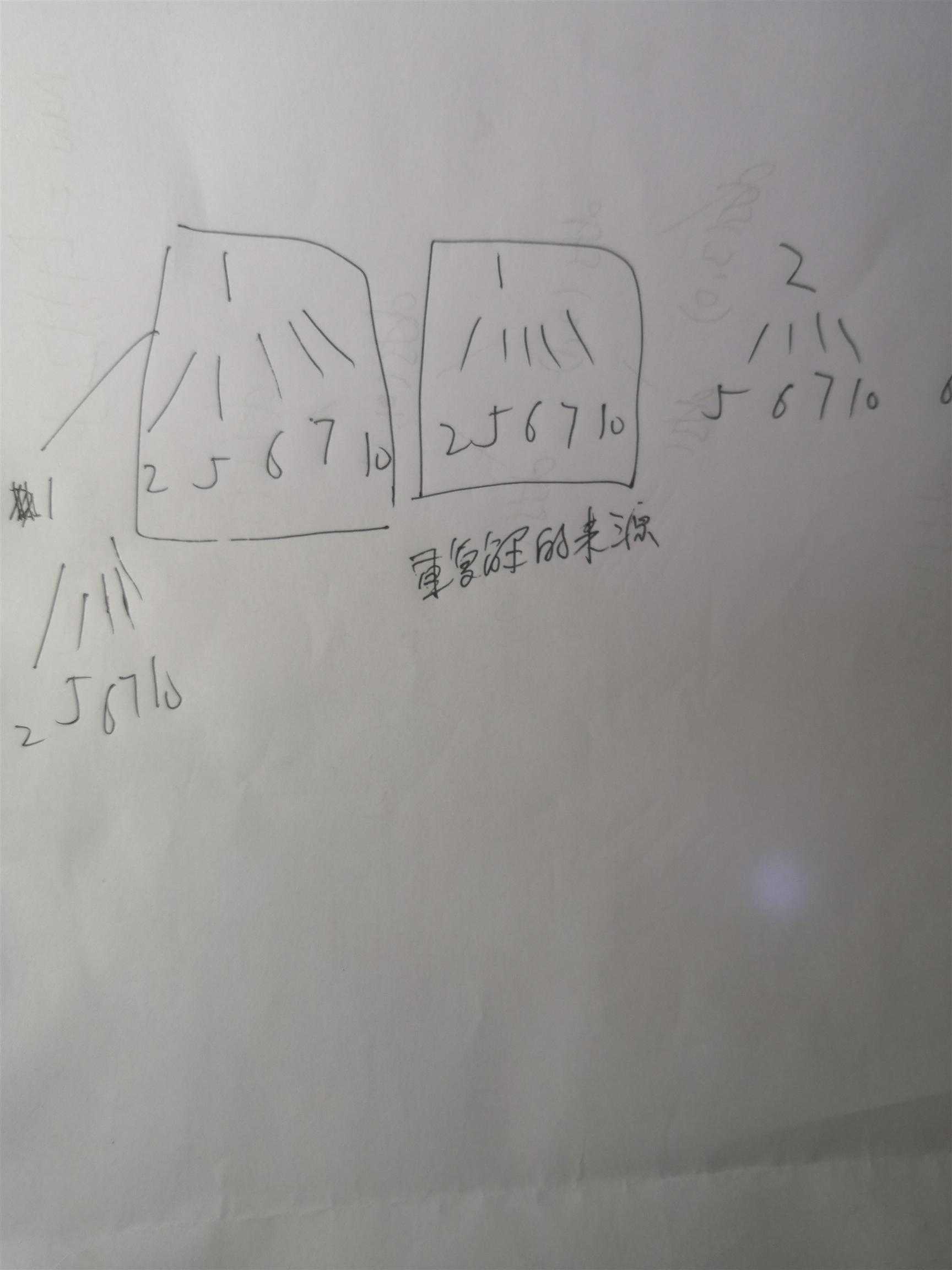
那么我们先对数组排序,得到1,1,2,5,6,7,10。每一次dfs函数里,我们循环查找能够选取的元素,我们第一次循环中选取了1,那么下次循环中我们就不能再选相邻的第二个1了,即我们要保证每层dfs中我们选取的元素不能有重复的。这也就保证了我们最终得到的每个解内部都是严格非降序的。也就不可能得到重复解了。
如下图,我们画出如下的递归图,可以发现如果第一层中我们选取第二个1,其下面的递归树是选取第一个1的递归树的子集!所以从这里做剪枝是最好的办法,从根源上杜绝了重复解的出现。
1 class Solution { 2 public: 3 vector<vector<int>> res; 4 vector<int> cur; 5 vector<vector<int>> combinationSum2(vector<int>& candidates, int target) { 6 sort(candidates.begin(),candidates.end());//先排序 7 dfs(0,target,candidates); 8 return res; 9 } 10 void dfs(int idx,int to_go,vector<int>& nums){ 11 //从idx开始继续选取可能的元素,to_go是距离目标值的差值 12 if(to_go==0){ 13 res.emplace_back(cur); 14 return; 15 } 16 if(idx>=nums.size()){ 17 return; 18 } 19 for(int i=idx;i<nums.size();++i){ 20 if(i>idx and nums[i]==nums[i-1]){//该层里不能选取一样的元素(剪枝) 21 continue; 22 } 23 if(nums[i]<=to_go){ 24 cur.emplace_back(nums[i]); 25 dfs(i+1,to_go-nums[i],nums);//注意这里选取i之后,递归的dfs从i+1开始选取 26 cur.pop_back(); 27 } 28 } 29 } 30 };
链接:https://leetcode-cn.com/problems/combination-sum-iii/
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
所有数字都是正整数。
解集不能包含重复的组合。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
这题我觉得比上一题简单。首先这道题也要求不存在重复数字,即选取了i之后,就不能再次选取i了。
另外本题的另一个新要求就是解的大小必须恰好是k,比如n=7,k=3的情况,[1,6],[2,5],[7]这样的解都不是有效解,因为长度不满足要求。
我采取的方法是最终放入结果数组时检查当前解的长度是否满足要求。不过还有优化的空间,提前剪枝:
1.如果已经确定之后剩下的元素全放入当前解,长度也不够k,那么就可以提前返回。
2.当前遍历到数字num(num<9),如果当前解加上num到9的元素和都不够n,那么也可以提前返回。
不过这道题数据很小,不必优化。
1 class Solution { 2 public: 3 vector<vector<int>> res; 4 vector<int> cur; 5 int k,n; 6 vector<vector<int>> combinationSum3(int k,int n) { 7 this->k=k,this->n=n; 8 dfs(1,n); 9 return res; 10 } 11 void dfs(int idx,int to_go){ 12 //从idx开始继续选取可能的元素,to_go是当前元素和距离n的差值 13 if(to_go==0 and cur.size()==k){ 14 res.emplace_back(cur); 15 return; 16 } 17 if(cur.size()>=k){//最多k个数的限制 18 return; 19 } 20 for(int i=idx;i<10;++i){ 21 if(i<=to_go){ 22 cur.emplace_back(i); 23 dfs(i+1,to_go-i);//注意这里选取i之后,递归的dfs从i+1开始选取 24 cur.pop_back(); 25 } 26 } 27 } 28 };

链接:https://leetcode-cn.com/problems/combination-sum-iv/
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
示例:
nums = [1, 2, 3] target = 4 所有可能的组合为: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1) 请注意,顺序不同的序列被视作不同的组合。 因此输出为 7。
进阶:
如果给定的数组中含有负数会怎么样?
问题会产生什么变化?
我们需要在题目中添加什么限制来允许负数的出现?
首先按照前面的题目照猫画虎写出dfs:
1 class Solution { 2 public: 3 int res=0; 4 int cur=0; 5 int combinationSum4(vector<int>& nums, int target) { 6 sort(nums.begin(),nums.end()); 7 dfs(target,nums); 8 return res; 9 } 10 void dfs(int to_go,vector<int>& nums){ 11 //to_go是距离目标值的差值 12 if(to_go==0){ 13 res+=1; 14 return; 15 } 16 for(int i=0;i<nums.size() and nums[i]<=to_go;++i){ 17 dfs(to_go-nums[i],nums);//注意这里选取i之后,递归的dfs又继续从i开始选取 18 } 19 } 20 };
然后英勇的超时了
看来这题需要动态规划,dfs无法AC。
DP思路其实很简单,对于[1,2,3]的数组,target=4。
那么我们可以把4看成不同加法的结果:
1+3,其中3的所有可能组合数我们已知;
2+2,其中2的可能组合数我们已知;
3+1;
可以用自顶向下带备忘录的方法,不过我一般习惯使用自底向上求解。
简单递推一下上面的例子:
1:只能1自己,所以dp[1]=1。
2:可以分为1+1,dp[1]=1,所有dp[2]+=1。另外2自己也可以,所以dp[2]+=1,等于2。
3:分为1+2,其中dp[2]=2,所以dp[3]+=2=2;分为2+1,其中dp[1]=1,dp[3]+=1,等于3;3自己也可以,加一,所以最终dp[3]=4。
4:分为1+3,dp[4]+4=4;2+2,dp[4]+2=6;3+1,dp[4]+1=7;最终dp[4]就等于7。
这题C++的整数溢出比较烦,而可以注意到最终题目返回的却是int。这说明如果某个dp[i]值我们算的超过了INT_MAX,那这个dp[i]最终一定用不上。所以我们简单的跳过不管就好了
1 class Solution { 2 public: 3 int combinationSum4(vector<int>& nums, int target) { 4 if(nums.empty()){return 0;} 5 vector<int> dp(target+1,0);//dp[i]:元素和为i的可能组合个数 6 sort(nums.begin(),nums.end()); 7 int min_val=nums[0]; 8 for(int cur=min_val;cur<=target;++cur){ 9 int i=0; 10 for(;i<nums.size() and nums[i]<cur and INT_MAX-dp[cur]>=dp[cur-nums[i]];++i){ 11 //如果超过了INT_MAX就不计算了,反正最后计算dp[target]肯定用不到 12 dp[cur]+=dp[cur-nums[i]]; 13 } 14 if(dp[cur]!=INT_MAX and i<nums.size() and nums[i]==cur){//cur自己单独也是一个解 15 dp[cur]+=1; 16 } 17 } 18 return dp[target]; 19 } 20 };
完结撒花????
leetcode四道组合总和问题总结(39+40+216+377)
原文:https://www.cnblogs.com/FdWzy/p/12377757.html