【Course】Machine learning：Week 1-Lecture1&Lecture2

一、Introduction

• 略

  二、Linear Regression with One Variable

• 0 Model

  本节课的问题是房价预测问题：
  

• 1 model and cost function

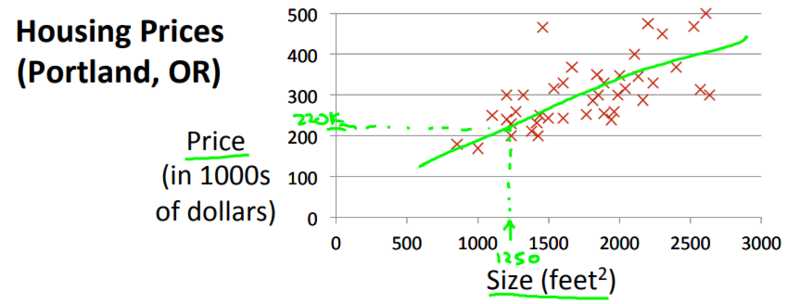
  Andrew Ng在cost function Intuition I中对hypothesis和cost function做了对比
  

  
  \(\theta_0\)已经假设等于0，于是只剩下一个参数\(\theta_1\)。

• hypothesis \(h_{\theta}(x)\)：是x的函数（对于一个固定的\(\theta_1\)）

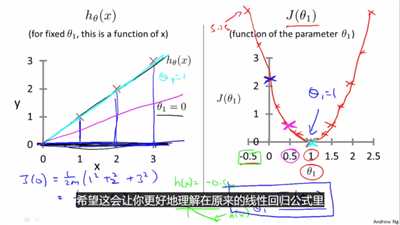
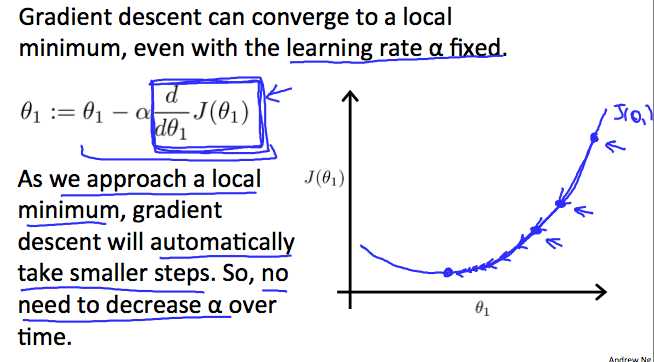
• cost function \(J(\theta_1)\)：是参数\(\theta_1\)的函数

• 2 Gradient Descent

• （1）针对这个单变量线性回归问题，如下图，有个要点：

  

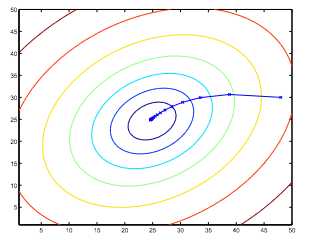
• \(\theta_1\)和\(\theta_2\)要同时更新，不然就会出错

• （2）梯度下降算法公式：

  \[\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1)\]
  无论\(\frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1)\)的符号是什么，\(\theta_1\)都会收敛到使得cost function取得最小值的点，符号是正时，\(\theta_1\)减小，符号是负时，\(\theta_1\)增大。

• （3）$\alpha的值要合理

  
• 此外

• （4）\(\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta_0, \theta_1)\)的推导过程

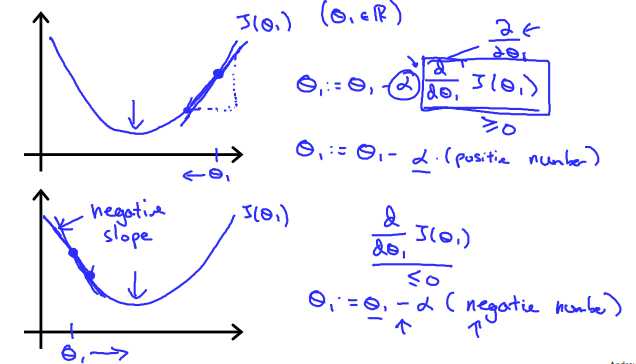
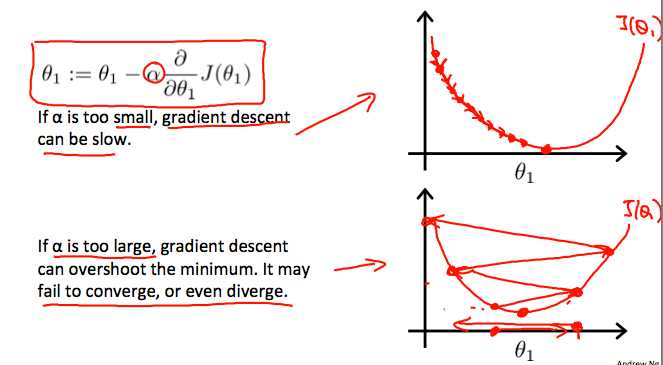
\[ \begin{aligned} \frac{\partial}{\partial \theta_{j}} J(\theta) &=\frac{\partial}{\partial \theta_{j}} \frac{1}{2}\left(h_{\theta}(x)-y\right)^{2} \&=2 \cdot \frac{1}{2}\left(h_{\theta}(x)-y\right) \cdot \frac{\partial}{\partial \theta_{j}}\left(h_{\theta}(x)-y\right) \&=\left(h_{\theta}(x)-y\right) \cdot \frac{\partial}{\partial \theta_{j}}\left(\sum_{i=0}^{n} \theta_{i} x_{i}-y\right) \&=\left(h_{\theta}(x)-y\right) x_{j} \end{aligned} \]

• （5）一个梯度下降的例子

  梯度下降的轨迹，初始值为(48,30)

【Course】Machine learning：Week 1-Lecture1&Lecture2

原文：https://www.cnblogs.com/Ireland/p/12383594.html