PCA/NLPCA
主成分分析(Principal Component Analysis,PCA), 是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。主成分分析首先是由K.皮尔森(Karl Pearson)对非随机变量引入的,尔后H.霍特林将此方法推广到随机向量的情形。信息的大小通常用离差平方和或方差来衡量
在用统计分析方法研究多变量的数据时,变量个数太多就会增加数据的复杂性。人们自然希望变量个数较少而得到的信息较多。在很多情形,变量之间是有一定的相关关系的,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此数据的信息有一定的重叠。主成分分析是对于原先提出的所有变量,将重复的变量(关系紧密的变量)删去多余,建立尽可能少的新变量,使得这些新变量是两两不相关的,而且这些新变量在反映数据的信息方面尽可能保持原有的信息。
PCA(主分量分析):
PCA用一系列直线来描述数据集中最为主要的一些变化趋势,其中每条直线都由观察变量的加权线性组合定义的。第一条直线(或称主成分),用来描述最主要的变化趋势:在保证和前期成分(直线)正交性(即不相关性)的同时,后续的成分(直线)描述尽可能大的变化趋势。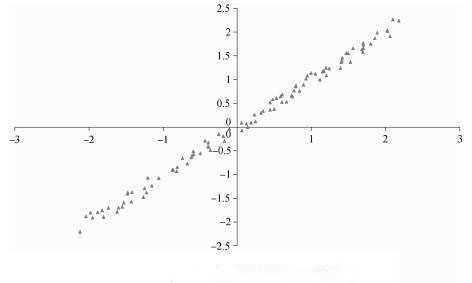
NLPCA(非线性主分量分析):
与PCA仅使用直线不同,非线性主成分分析NLPCA使用若干条开放曲线或闭合曲线来描述数据集的变化趋势。闭合曲线(如圆环),是一条首尾相接无端点的曲线。图3.2为一条开放曲线。可见,NLPCA具有使用较低维度的空间描述非线性问题的能力。
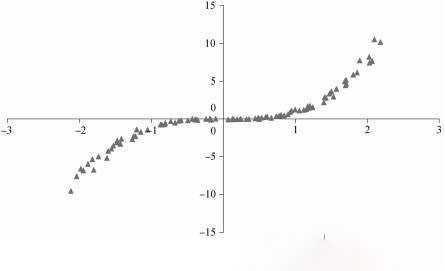
区别意义:
PCA实际计算中只涉及到输入数据概率密度分布函数(Pdf)的二阶特性(协方差矩阵),所以解出的各主分量只互相正交(不相关),但并不满足相互独立。而且信号的大部分重要特征往往包含在Pdf的高阶统计特性中,所以只有观测数据是服从高斯分布的源信号构成,PCA方法才有效。NLPCA即将高阶累积量引入标准的PCA中。高阶累积量引入计算,则可以处理非高斯分布的信号,适用于很多富有挑战性的问题。
附github大神代码下载地址:https://codeload.github.com/bavdekar/pca/zip/master
————————————————
版权声明:本文为CSDN博主「柒一水」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/qq_28156907/article/details/102895757
原文:https://www.cnblogs.com/sggggr/p/12392676.html