深度学习之正向传播、反向传播和计算图——2020.3.1

一、正向传播

（ 一 ） 定义

?????正向传播是指对神经?络沿着从输?层到输出层的顺序，依次计算并存储模型的中间变量（包括输出）。为简单起?，假设输?是?个特征为 \(x \in R^d\) 的样本，且不考虑偏差项，那么中间变量:
\[z = W^{(1)}x\]
其中 \[W^{(1)} \in R^{h \times d}\]是隐藏层的权重参数。把中间变量 \(z \in R^h\) 输?按元素运算的激活函数$ \phi$后，将得到向量?度为 \(h\)的隐藏层变量:
\[h = \phi \left( z \right)\]
隐藏层变量 \(h\)也是?个中间变量。假设输出层参数只有权重 \(W^{(2)} \in R^{q \times h}\) ，可以得到向量?度为 \(q\) 的输出层变量
\[o = W^{(2)}h\]

假设损失函数为 \(l\)，且样本标签为 \(y\)，可以计算出单个数据样本的损失项
\[L = l(o,y)\]
根据 \(L_2\)范数正则化的定义，给定超参数 \(\lambda\)，正则化项即

\[s=\frac{\lambda}{2} \left( ||W^{(1)}||^2_F + ||W^{(2)}_F|| \right)\]
其中矩阵的Frobenius范数等价于将矩阵变平为向量后计算 \(L_2\) 范数。最终，模型在给定的数据样本上带正则化的损失为:

\[J = L+s\]
将 \(J\) 称为有关给定数据样本的?标函数。

（ 二 ）正向传播的计算图

?????可通过绘制计算图来可视化运算符和变量在计算中的依赖关系。例如前节softmax回归实现中，绘制的样例模型正向传播的计算图，其中左下?是输?，右上?是输出。可以看到，图中箭头?向?多是向右和向上，其中?框代表变量，圆圈代表运算符，箭头表示从输?到输出之间的依赖关系。

二、反向传播

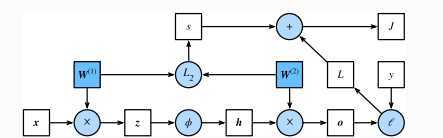
?????反向传播指的是计算神经?络参数梯度的?法。总的来说，反向传播依据微积分中的链式法则，沿着从输出层到输?层的顺序，依次计算并存储?标函数有关神经?络各层的中间变量以及参数的梯度。
?????关于反向传播的计算，主要会用到链式法则。

深度学习之正向传播、反向传播和计算图——2020.3.1

原文：https://www.cnblogs.com/somedayLi/p/12392521.html