题目-数字在排序数组中出现的次数
统计一个数字在排序数组中出现的次数。
如Input:
array=1,2,3,3,3,3,4,6
k=3
Output:
4
思路
1.由于输入的数组是排序的,那么二分查找算法很适用这个场景。二分查找很容易找到一个3,由于3可能出现很多次,因此我们可以在3的左右两边按顺序扫描,分别找到第一个3和最后一个3.
因为要查找的数字在长度为n的数组中有可能出现O(n)次,所以顺序扫描的时间复杂度为O(n)
2.优化的解法是:用二分查找算法直接找到第一个k和最后一个k
思路就是:(以找到第一个k为例)二分查找总是拿数组中间的数字和k作比较,如果中间的数字比k大,那么k只有可能出现在数组的前半段,下一轮只要在数组的前半段查找就好了。反之。
如果中间数字==k,那么先判断这个数字是不是第一个k。如果位于中间数字的前一个数不是k,那么说明中间数就是第一个k;如果前一个数也是k,说明第一个k肯定在数组的前半段,下一轮依然需要在数组的前半段查找。
这样查找第一个k和最后一个k都是,使用二分查找法在数组中查找一个合乎要求的数字,时间复杂度都是O(logn)。
解法
public class Solution { public int GetNumberOfK(int [] array , int k) { if(array.length == 0) return 0; int left=0; int right=array.length-1; int index=0; //二分查找,找到靠中间的那个k while(left<right){ int mid = (left+right)/2; if(array[mid] == k){ index = mid; break; } else if(array[left]<array[mid]){ left = mid+1; } else{ right = mid-1; } } //遍历查找k int count=0; //从找到的index,往前查找 for(int i=index; i>=0 && array[i]==k; i--) count++; //从找到的index,往后查找 for(int i=index+1; i<array.length && array[i]==k; i++) count++; return count; } }
题目-二叉树的深度
输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
思路
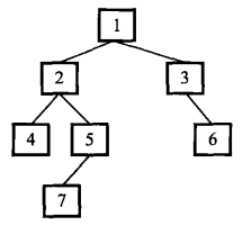
(该树的深度为4,由于从根结点到叶结点最长的路径包含4个结点)
如果一棵树只有一个结点,那么深度为1;
如果根结点只有左子树没有右子树,那么树的深度应该是左子树深度+1;
反之,深度应该是右子树深度+1;
如果既有左子树又有右子树,那么就是深度的较大值+1.
可以使用递归来实现。
解法
/** public class TreeNode { int val = 0; TreeNode left = null; TreeNode right = null; public TreeNode(int val) { this.val = val; } } */ public class Solution { public int TreeDepth(TreeNode root) { if(root == null) return 0; int left = TreeDepth(root.left); int right = TreeDepth(root.right); return (left>right)?(left+1):(right+1); } }
题目-平衡二叉树
输入一棵二叉树,判断该二叉树是否是平衡二叉树。
思路
平衡二叉树的概念是:如果某二叉树中任意结点的左右子树的深度相差不超过1。
1.最简单的思路就是直接在遍历树的每个结点的时候,调用上面的求树深度的函数得到结点的 左右子树 的深度。如果某结点的左右子树深度相差超过1,则不是平衡树。
这种方式出现一个结点会被重复遍历多次的情况,导致时间效率不高。
2.因此考虑每个结点只遍历一次的解法
如果用后序遍历的方式遍历二叉树的每个结点,在遍历到一个结点之前,已经遍历到它的左右子树。
那么只要在遍历每个结点的时候记下它的深度,就可以一边遍历一边判断每个结点是不是平衡的。
解法
public class Solution { private boolean isBalanced=true; public boolean IsBalanced_Solution(TreeNode root) { height(root); return isBalanced; } private int height(TreeNode root){ if(root==null || !isBalanced) return 0; int left = height(root.left); int right = height(root.right); //平衡树中任意结点的左右子树的深度相差不超过1 if(Math.abs(left-right)>1) isBalanced = false; return 1+Math.max(left, right); } }
题目-数组中只出现一次的数字
一个整型数组里除了两个数字之外,其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。
思路
1.我们首先可以考虑如果只有一个数字出现了一次,那么考虑异或的性质:任何一个数字异或它自己都等于0.即从头到尾遍历数组,最后的结果是只出现一次的数字,成对出现两次的数字全部在异或中抵消了。
2.那么有了上面的思路。对于原题,我们可以试图把原数组拆分成两个子数组,使每个子数组包含一个只出现一次的数字,其他数字都承兑出现两次。
3.那么如何这样拆分数组呢?
由于不相同的元素在位级表示中必定会有一位不同,那么所有元素异或得到的结果是 不存在重复的两个元素异或的结果。也就是这个结果 的二进制表示中 至少有一位 为1,我们在结果数字中找到第一个为1的位的位置,记为n。
以第n位是不是1为标准,把原数组中的数字分为两个子数组。第一个子数组中每个数字的第n位都是1,而第二个子数组中每个数字的第n位都是0.
diff &= -diff 得到出 diff 最右侧不为 0 的位,也就是不存在重复的两个元素在位级表示上最右侧不同的那一位,利用这一位就可以将两个元素区分开来。
解法
//num1,num2分别为长度为1的数组。传出参数 //将num1[0],num2[0]设置为返回结果 public class Solution { public void FindNumsAppearOnce(int [] array,int num1[] , int num2[]) { int diff=0; //相同的数字异或为0,0与其他数字异或得到原数字 //全部异或运算得到一个值,此时结果一定非0 for(int num:array){ diff^=num; } //得到diff最右侧不为0的位,也就是不存在重复的两个元素在位级表示上最右侧不同的那一位,利用这一位可以将两个元素区分开 //即得到该值二进制最低位1的位置index diff &= -diff; //按照最低位index是0/1把原数组分为两组 //每组进行连续异或运算得到只出现一次的数字,因为相同的数会得0 for(int num:array){ if((num&diff)==0) num1[0]^=num; else num2[0]^=num; } } }
题目-和为S的两个数字
输入一个递增排序的数组和一个数字S,在数组中查找两个数,使得他们的和正好是S,如果有多对数字的和等于S,输出两个数的乘积最小的。
思路
使用两个指针,一个指向数组头,一个指向数组尾。
头指针往后遍历,尾指针向前遍历。
不断收拢两个指针的间距,直到符合和为S的要求。
如果多对,需要输出乘积最小的,由于是从头尾开始查找,当前满足条件的头指针位置一定是最小的。因此能得到乘积最小。
解法
import java.util.ArrayList; public class Solution { public ArrayList<Integer> FindNumbersWithSum(int [] array,int sum) { ArrayList<Integer> ret = new ArrayList<Integer>(); if(array==null) return ret; int start=0,end=array.length-1; while(start<end){ int curSum=array[start]+array[end]; //如果和大于,则减小 if(curSum>sum){ end--; } //如果小于,则加 else if(curSum<sum){ start++; } else{ ret.add(array[start]); ret.add(array[end]); break; } } return ret; } }
题目-和为S的连续正数序列
小明很喜欢数学,有一天他在做数学作业时,要求计算出9~16的和,他马上就写出了正确答案是100。但是他并不满足于此,他在想究竟有多少种连续的正数序列的和为100(至少包括两个数)。没多久,他就得到另一组连续正数和为100的序列:18,19,20,21,22。现在把问题交给你,你能不能也很快的找出所有和为S的连续正数序列? Good Luck!
思路
借鉴上题的经验,那我们同样也可以以int设置两个指针start,end,分别表示序列的最小值和最大值。
如果序列之和大于S,那么就从序列中去除较小的数,就增大start的值;
如果和小于S,那么就增加end,在序列中增加更多的数字。
如果和==S,那么就是找到一个序列。首先把它添加进去,然后再增加end和start,把整个序列往后移动一位。再次进行比较和查找
解法
import java.util.ArrayList;
public class Solution {
public ArrayList<ArrayList<Integer> > FindContinuousSequence(int sum) {
ArrayList<ArrayList<Integer>> ret = new ArrayList<>();
int start = 1,end = 2;
int curSum = 3;
while(end < sum){
//大于sum,则从序列中去掉较小的值。也就是当前的start增大
if(curSum > sum){
curSum=curSum-start;
start++;
}
//小于sum,那么需要让序列包含更多的数字
else if(curSum < sum){
end++;
curSum=curSum+end;
}
//找到一个序列
else{
ArrayList<Integer> list = new ArrayList<>();
//由于是连续序列,把序列中的数字加到list中
for(int i=start; i<=end; i++){
list.add(i);
}
ret.add(list);
curSum=curSum-start;
start++;
end++;
curSum=curSum+end;
}
}
return ret;
}
}
题目-左旋转字符串
汇编语言中有一种移位指令叫做循环左移(ROL),现在有个简单的任务,就是用字符串模拟这个指令的运算结果。对于一个给定的字符序列S,请你把其循环左移K位后的序列输出。例如,字符序列S=”abcXYZdef”,要求输出循环左移3位后的结果,即“XYZdefabc”。是不是很简单?OK,搞定它!
思路
对于这个,我们可以列出字符串及其旋转后的效果。那么我们可以发现一些规律:
比如对于序列S="abcXYZdef",可以将其分为两部分,前面的3个字符为第一部分,后面的为第二部分。
然后我们分别反转这两部分,变成cba和fedZYX。
那么再将整个字符串旋转,得到左移3位的效果,“XYZdefabc”
(注意在java中,为了处理单个字符,我们通常需要把String类型转化为char[] )
解法
public class Solution { public String LeftRotateString(String str,int n) { if(str.length() <= n){ return str; } char[] chars = str.toCharArray(); reverse(chars, 0, n-1); reverse(chars, n, str.length()-1); reverse(chars, 0, str.length()-1); return new String(chars); } private void reverse(char[] chars, int i, int j){ while(i<j){ swap(chars, i++, j--); } } private void swap(char[] chars, int i, int j){ char temp = chars[i]; chars[i] = chars[j]; chars[j] = temp; } }
题目-翻转单词顺序列
牛客最近来了一个新员工Fish,每天早晨总是会拿着一本英文杂志,写些句子在本子上。同事Cat对Fish写的内容颇感兴趣,有一天他向Fish借来翻看,但却读不懂它的意思。例如,“student. a am I”。后来才意识到,这家伙原来把句子单词的顺序翻转了,正确的句子应该是“I am a student.”。Cat对一一的翻转这些单词顺序可不在行,你能帮助他么?
思路
整个题与上一题类似。
同样是使用翻转,那么可以把这个翻转拆分为两步:
1.把每个单词都翻转,使用start和end记录当前这个单词的位置,也就是需要翻转的位置。
2.把整个句子翻转
3.这个翻转过程需要注意:只有一个单词的情况;有标点符号的情况
解法
public class Solution { public String ReverseSentence(String str) { if(str==null){ return null; } int n = str.length(); char[] chars = str.toCharArray(); //记录要反转单词的起始位置 int start=0, end=0; for(end=0; end<=n; end++){ if(end == n || chars[end] == ‘ ‘){ reverse(chars, start, end-1); start = end+1; } } reverse(chars, 0, n-1); return new String(chars); } private void reverse(char[] chars, int i, int j){ while(i<j){ swap(chars, i++, j--); } } private void swap(char[] chars, int i, int j){ char temp = chars[i]; chars[i] = chars[j]; chars[j] = temp; } }
题目-扑克牌顺子
LL今天心情特别好,因为他去买了一副扑克牌,发现里面居然有2个大王,2个小王(一副牌原本是54张^_^)...他随机从中抽出了5张牌,想测测自己的手气,看看能不能抽到顺子,如果抽到的话,他决定去买体育彩票,嘿嘿!!“红心A,黑桃3,小王,大王,方片5”,“Oh My God!”不是顺子.....LL不高兴了,他想了想,决定大\小 王可以看成任何数字,并且A看作1,J为11,Q为12,K为13。上面的5张牌就可以变成“1,2,3,4,5”(大小王分别看作2和4),“So Lucky!”。LL决定去买体育彩票啦。 现在,要求你使用这幅牌模拟上面的过程,然后告诉我们LL的运气如何, 如果牌能组成顺子就输出true,否则就输出false。为了方便起见,你可以认为大小王是0。
思路
1.怎么判断数字是不是连续呢,直观的方法就是将数组排序。
2.由于有癞子的存在,那么可以用癞子(0)去填补数组中的空缺,如果排序后的数组不是连续的,也就是相邻的数字间隔若干个数字,只要我们有足够多的癞子,那就可以去填补这个空缺。
3.那么总结起来过程就是:1)数组排序;2)统计数组中0的个数;3)最后统计排序后的数组中相邻数字间的空缺;4)判断0是否足够去填补空缺。
4.需要注意的是,顺子中不能出现对子,也就是不能出现重复的数字。
解法
import java.util.Arrays; public class Solution { public boolean isContinuous(int [] numbers) { if(numbers.length < 5){ return false; } Arrays.sort(numbers); //统计大小王,当成癞子 int cnt=0; for(int num:numbers){ if(num==0){ cnt++; } } //使用癞子补全顺子 for(int i=cnt;i<numbers.length-1;i++){ //存在相同的数字,那么就不是顺子 if(numbers[i+1] == numbers[i]) return false; cnt-=numbers[i+1]-numbers[i]-1; } //如果能剩下癞子,或刚好够补,那么则是顺子 return cnt>=0; } }
题目-孩子们的游戏(圆圈中最后剩下的数)
每年六一儿童节,牛客都会准备一些小礼物去看望孤儿院的小朋友,今年亦是如此。HF作为牛客的资深元老,自然也准备了一些小游戏。其中,有个游戏是这样的:首先,让小朋友们围成一个大圈。然后,他随机指定一个数m,让编号为0的小朋友开始报数。每次喊到m-1的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续0...m-1报数....这样下去....直到剩下最后一个小朋友,可以不用表演,并且拿到牛客名贵的“名侦探柯南”典藏版(名额有限哦!!^_^)。请你试着想下,哪个小朋友会得到这份礼品呢?(注:小朋友的编号是从0到n-1) 如果没有小朋友,请返回-1
思路
1.这是一个经典的约瑟夫环问题,那么通过分析每次被删除的数字的规律 来直接计算圆圈中剩下的数字。
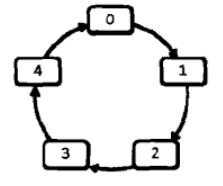

最后得到一个递归公式:
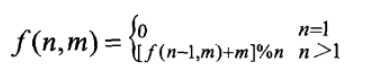
要得到n个数字的序列中最后剩下的数,只需要得到n-1个数字的序列中最后剩下的数字。以此类推。
2.模拟小朋友退出游戏的过程,用LinkedList链表来表示圆圈。然后每次按照要求删除结点,((removeIndex+m-1)%list.size();)
解法
//解法1
import java.util.LinkedList; public class Solution { public int LastRemaining_Solution(int n, int m) { if(n == 0) return -1; if(n == 1){ return 0; } int last=0; for(int i=2; i<=n; i++) last=(last+m)%i; return last; }
//解法2
import java.util.LinkedList; public class Solution { public int LastRemaining_Solution(int n, int m) { if(n<1 || m<1){ return -1; } LinkedList<Integer> list = new LinkedList<Integer>(); for(int i=0;i<n;i++){ list.add(i); } //当前删除的结点下标 int removeIndex=0; while(list.size()>1){ //下一个要删除的结点的下标 removeIndex=(removeIndex+m-1)%list.size(); list.remove(removeIndex); } return list.getFirst(); } }
原文:https://www.cnblogs.com/lyeeer/p/12397869.html