最小乘积模型

最小乘积模型

每种物品有两个权值\(a_i,b_i\)，求选出\(k\)个物品，使得\(\sum{a_i}*\sum{b_i}\)最小

考虑先求出\(\sum{a_i}\)和\(\sum{b_i}\)最小的两种方案，记为\(A,B\)

我们将\(\sum{a_i}\)和\(\sum{b_i}\)看作两个坐标，则\(A,B\)可以看作二维平面上的两个点

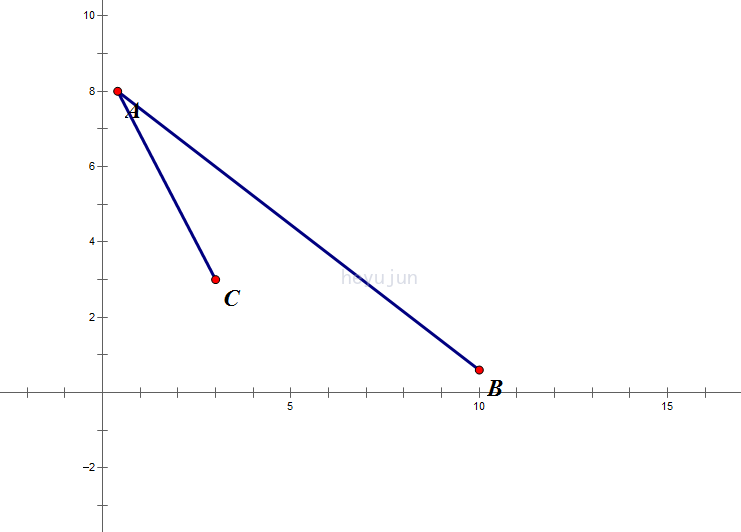
据说图片来自\(hyj\)的\(blog\)，侵删

我们发现我们要找的点应该是位于\(A,B\)的左下方，且\(S_{ABC}\)最大的点

根据\(S_{ABC}=-\frac{AB×AC}{2}\)（此处是叉积）

可以得出我们要让\(AB\)与\(AC\)的叉积最小（因为是负数）

化简一下

\[AB×AC=(x_B??x_A?)(y_C??y_A?)?(x_C??x_A?)(y_B??y_A?)=(x_B-x_A)*y_C+(y_A-y_B)*x_C-(x_B-x_A)*y_A+(y_B-y_A)*x_A\]

发现后两项中没有\(C\)，我们将物品权值改为\(c_i=(x_B-x_A)*b_i+(y_A-y_B)*a_i\)

然后求最小\(\sum{c_i}\)，递归到\(AB×AC\ge 0\)为止

例题

#include<bits/stdc++.h>
using namespace std;
namespace red{
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define mid ((l+r)>>1)
    inline int read()
    {
        int x=0;char ch,f=1;
        for(ch=getchar();(ch<'0'||ch>'9')&&ch!='-';ch=getchar());
        if(ch=='-') f=0,ch=getchar();
        while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();} 
        return f?x:-x;
    }
    const int N=1e4+10;
    int n,m,suma,sumb;
    struct point
    {
        int x,y,a,b,c;
        inline bool operator < (const point &t) const{ return c<t.c; }
    }a[N];
    struct node
    {
        int x,y;
        inline node operator - (const node &t) const
        {
            return (node){x-t.x,y-t.y};
        }
        inline int cross(const node &t) const
        {
            return x*t.y-y*t.x;
        }
    }A,B,ret;
    int f[N];
    inline int find(int k){return f[k]==k?k:f[k]=find(f[k]);}
    inline node kruskal()
    {
        for(int i=1;i<=n;++i) f[i]=i;
        sort(a+1,a+m+1);
        int suma=0,sumb=0,tot=0;
        for(int i=1;i<=m;++i)
        {
            int x=find(a[i].x),y=find(a[i].y);
            if(x==y) continue;
            f[x]=y;
            suma+=a[i].a,sumb+=a[i].b;
            if(++tot==n-1) break;
        }
        if(1ll*suma*sumb<1ll*ret.x*ret.y||(1ll*suma*sumb==1ll*ret.x*ret.y&&suma<ret.x)) ret.x=suma,ret.y=sumb;
        return (node){suma,sumb};
    }
    inline void solve(node A,node B)
    {
        for(int i=1;i<=m;++i)
            a[i].c=(B.x-A.x)*a[i].b+(A.y-B.y)*a[i].a;
        node C=kruskal();
        if((B-A).cross(C-A)>=0) return;
        solve(A,C),solve(C,B);
    }
    inline void main()
    {
        n=read(),m=read();
        for(int i=1;i<=m;++i)
            a[i].x=read()+1,a[i].y=read()+1,a[i].a=a[i].c=read(),a[i].b=read();
        ret.x=ret.y=1e9+7;
        A=kruskal();
        for(int i=1;i<=m;++i) a[i].c=a[i].b;
        B=kruskal();
        solve(A,B);
        printf("%d %d",ret.x,ret.y);
    }
}
signed main()
{
    red::main();
    return 0;
}

最小乘积模型

原文：https://www.cnblogs.com/knife-rose/p/12404044.html