大数定律:实验条件不变的情况下,重复试验N次,随机事件的频率近似它的频率。
通过掷骰子进行模拟:一枚骰子出现1-6各个数字的概率都是1/6,我们通过生成1-6的随机数字,统计各个数字出现的频率是否近似这个概率。
import random import collections ‘‘‘ 实验条件不变的条件下,重复试验多次,随机事件的频率近似它的频率. 以掷骰子为例,1-6出现的概率都是1/6. ‘‘‘ list_num = [i*random.randint(1,6)/i for i in range(100000) if i>0] c = collections.Counter(list_num) print(c)
通过random模块中的randint()生成[1,6]范围内的随机整数,循环10万次。通过列表解析,生成列表。
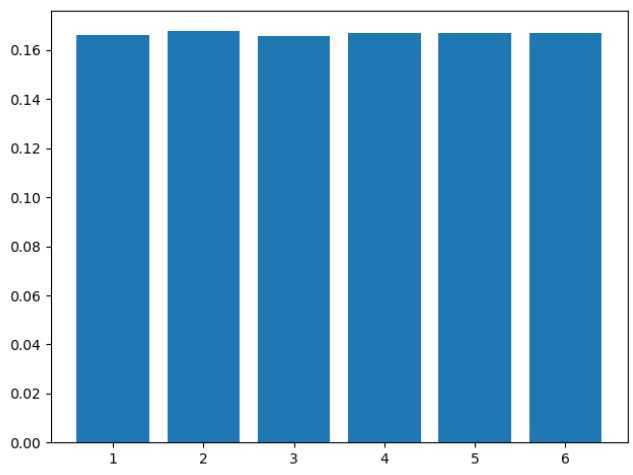
通过collections中的Couter函数,统计列表中相同元素出现的次数,即1-6各个数字出现的次数。返回的是字典形式的统计结果,通过肉眼观察,出现的次数几乎都是在1.6万次上。
Counter({4.0: 16786, 2.0: 16722, 5.0: 16683, 1.0: 16643, 6.0: 16635, 3.0: 16530})
出现的频率:
原文:https://www.cnblogs.com/liuhuacai/p/12404823.html