? 支持向量机(Support Vector Machine,以下简称SVM),是一个二元分类( dualistic classification)的广义线性分类器(generalized linear classifier),通过寻找分离超平面作为决策边界(decision boundary),分离少量的支持向量(support vector),从而达到分类目的\([1][2][3]\)。
? 可采用一对一(One Versus One)、一对多(One Versus Rest)等策略转变为多分类问题\([6]\)。
? 原问题(primal problem)仅支持硬间隔最大化(hard margin maximum),添加松弛变量(slack variable)后支持软间隔最大化(soft margin maximum)。
? 属性:稀疏性和稳健性(Robust)\([1]\)、非参数模型(nonparametric models)、监督学习(supervised learning)、判别模型(discriminant model)、【KKT条件(Karush-Kuhn-Tucker condition)约束,对偶形式(dual form)转换,序列最小优化(Sequential Minimal Optimization,以下简称为SMO)算法求解\([1][4][5]\)】、支持核方法(kernel method)。
? 求解:使用门页损失函数(hinge loss function)计算经验风险(empirical risk)并在求解时加入了正则化项以优化结构风险(structural risk),1.直接进行二次规划(Quadratic Programming)求解;2.利用拉格朗日算子( Lagrange multipliers),将其转为,符合KKT条件(Karush-Kuhn-Tucker condition)的对偶形式(dual form),再进行二次规划(Quadratic Programming)求解\([1]\)。
? 扩展:利用正则化、概率学、结构化、核方法改进算法,包括偏斜数据、概率SVM、最小二乘SVM(Least Square SVM, LS-SVM)、结构化SVM(structured SVM)、多核SVM(multiple kernel SVM);也可扩充到回归(Support Vector Regression)、聚类、半监督学习(Semi-Supervised SVM, S3VM)。
当样本数据集线性可分(linear separable)时,寻找正负样本中各自距离对方最近的样本数据(称为支持向量,即SVM的名字由来)(一般为三个),利用相对位置(排除坐标缩放影响,也是采用几何间隔的原因),构建最大间隔(几何间隔)进行分类[3]。
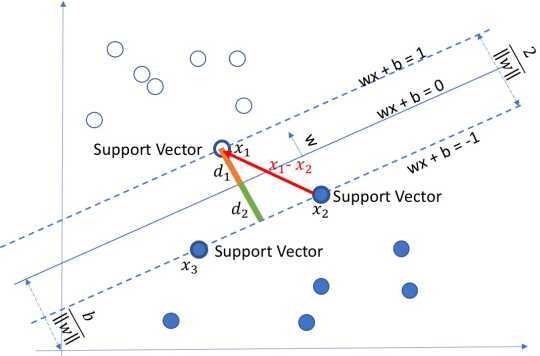
\[from:greedyai.com\]
如图,当硬间隔最大化时,正类支持向量(positive support vector)(图中\(x_1\))与负类支持向量(negative support vector)(图中\(x_2, x_3\))使
\(sign\)表示符号函数,即计算括号内的值,值为正数则取正类别,反之亦然。
(求解推导请查看下方dual problem内容)
? 硬间隔最大化无法满足实际条件中,异常值间隔、线性不可分等情况,因此引入软间隔(soft margin)方式: 在原问题基础上,添加松弛变量(slack variable),增加容错率。
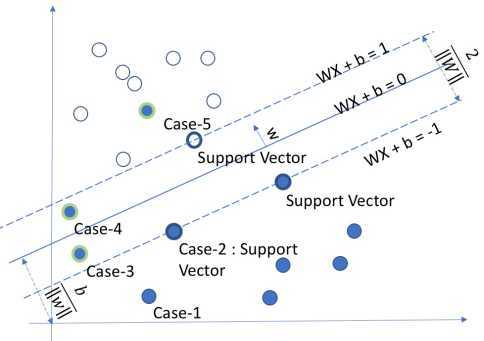
\[from:greedyai.com\]
(求解推导请查看下方dual problem内容)
成立条件:
内容(具体问题中有不同表现形式):
\[
\begin{cases}
\frac{\partial }{\partial w_i}L(w^\star,\alpha^\star,\beta^\star)=0 & i=1,\dots,d \\frac{\partial }{\partial \beta_i}L(w^\star,\alpha^\star,\beta^\star)=0 & i=1,\dots,l \{\color{red}{\alpha^\star g_i(w^\star)=0}}& i=1,\dots,k\g_i(w^\star)\leq 0 & i=1,\dots,k \\alpha^\star \geq 0 & i=1,\dots,k \\end{cases}
\rightarrow
\alpha^\star>0, g_i(w^\star)=0
\]
留意\(\alpha^\star>0, g_i(w^\star)=0\),即非支持向量的样本令\(g_i(w^\star)\neq 0\),可得\(\alpha^\star=0\);
原优化问题:
\[
\begin{align}
&min_w\;f(w) \s.t.
&g_i(w)\leq 0 \&h_i(w)=0
\end{align}
\]
(from greedyai.com)
\[ \begin{align} &min_{(w,b)}\,\frac{1}{2}\|W\|^2 \s.t. &y_i(W^{\top}x_i+b)\geq 1 \end{align} \]
改造:符合对偶形式一般流程(dual form normal processing)
\[
\begin{align}
g_i(w)=
-y_i(W^{\top}x_i+b)+1
\leq 0
\end{align}
\]
转换:拉格朗日函数
\[
\begin{align}
{\cal{L}(w,\alpha,\beta)}
&=
f(w) +
\sum_{i=1}^k\alpha_ig_i(w)+
\sum_{i=1}^l\beta_ih_i(w) \&=\frac{1}{2}\|W\|^2-
\sum_{i=1}^n\alpha_i[y_i(W^{\top}x_i+b)-1]
\end{align}
\]
去除:未知值\(w,b\)求解
\[
\begin{align}
\nabla_w{\cal{L}(w,b,\alpha,\beta)}
&=\nabla_w\large[\frac{1}{2}\|W\|^2-
\sum_{i=1}^n\alpha_i[y_i(W^{\top}x_i+b)-1]\large] \&=w-\sum_{i=1}^n\alpha_iy_ix_i
{\color{red}{\rightarrow0}} \\rightarrow w
&=\sum_{i=1}^n\alpha_iy_ix_i
\tag{3.1} \\nabla_b{\cal{L}(w,b,\alpha,\beta)}
&=\nabla_b\large[\frac{1}{2}\|W\|^2-
\sum_{i=1}^n\alpha_i[y_i(W^{\top}x_i+b)-1]\large] \&=\sum_{i=1}^n\alpha_iy_i
{\color{red}{\rightarrow0}}
\tag{3.2} \\end{align}
\]
代入:将\(3.1,3.2\)代入拉格朗日函数
\[
\begin{align}
{\cal{L}(w,b,\alpha,\beta)}
&=
\frac{1}{2}[\sum_{i=1}^n\alpha_iy_ix_i]^2-
\sum_{i=1}^n\alpha_i[y_i(\sum_{i=1}^n\alpha_jy_jx_ix_j+b)-1] \&=
\frac{1}{2}\sum_{i=1}^n\alpha_i\alpha_jy_iy_jx_ix_j-
\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_ix_j-b\sum_{i=1}^n\alpha_iy_i+
\sum_{i=1}^n\alpha_i \&=
-\frac{1}{2}\sum_{i=1}^n\alpha_i\alpha_jy_iy_jx_ix_j-
0+
\sum_{i=1}^n\alpha_i \&=
\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\alpha_i\alpha_jy_iy_jx_ix_j
\tag{3.3}
\end{align}
\]
dual问题:
\[
\begin{align}
max_\alpha\;W(\alpha)
&=
\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\alpha_i\alpha_jy_iy_jx_ix_j \s.t.\;
&\alpha_i\geq 0 \&\sum_{i=1}^n\alpha_iy_i=0
\end{align}
\]
推导\(b\):(homework)
\[
\begin{align}
b=-\frac{1}{2}
(max_{i:y_i=-1}W^\top x_i+min_{i:y=1}W^\top x_i)
\end{align}
\]
决策子:
\[
\begin{align}
f(w)
&=
W^\top x+b \&=(\sum_{i=1}^n\alpha_iy_ix_i)x-
\frac{1}{2}
(max_{i:y_i=-1}W^\top x_i+min_{i:y=1}W^\top x_i) \\end{align}
\]
补充:当前形式的KKT条件(参考\([9]\) -1)
\[
\begin{cases}
&\alpha_i&=&0 &\Rightarrow
&y_i(W^{\rm{T}}x+b) &\geq 1 \&\alpha_i&>&0 &\Rightarrow
&y_i(W^{\rm{T}}x+b)&= 1 \\end{cases}
\]
由KKT condition分析,知:
(from greedyai.com)4:19
\[ \begin{align} &min_{(w,b,\color{red}{\xi\geq 0})}\,\frac{1}{2}\|W\|^2+\color{red}{C\sum_{i}\xi_i} \s.t. &y_i(W^{\rm{T}}x_i+b)\geq 1\color{red}{-\xi_i} \end{align} \]
改造:符合对偶形式一般流程(dual form normal processing)
\[
\begin{align}
g_i(w)=
-y_i(W^{\top}x_i+b)+1{\color{red}{-\xi_i}}
\leq 0
\end{align}
\]
转换:拉格朗日函数
\[
\begin{align}
{\cal{L}(w,\alpha,\beta)}
&=
f(w) +
\sum_{i=1}^k\alpha_ig_i(w)+
\sum_{i=1}^l\beta_ih_i(w) \&=\frac{1}{2}\|W\|^2+{\color{red}{C\sum_{i}\xi_i}}-
\sum_{i=1}^n\alpha_i[y_i(W^{\top}x_i+b)-1{\color{red}{+\xi_i}}]
\end{align}
\]
去除:未知值\(w,b,\xi\)求解
\[
\begin{align}
\nabla_w{\cal{L}(w,b,\xi,\alpha,\beta)}
&=w-\sum_{i=1}^n\alpha_iy_ix_i
{\color{red}{\rightarrow0}} \\rightarrow w
&=\sum_{i=1}^n\alpha_iy_ix_i
\tag{3.4} \\nabla_b{\cal{L}(w,b,\xi,\alpha,\beta)}
&=\sum_{i=1}^n\alpha_iy_i
{\color{red}{\rightarrow0}}
\tag{3.5} \\nabla_\xi{\cal{L}(w,b,\xi,\alpha,\beta)}
&=\nabla_\xi\large[\frac{1}{2}\|W\|^2+\color{red}{C\sum_{i}\xi_i}\&\qquad -\sum_{i=1}^n\alpha_i[y_i(W^{\top}x_i+b)-1+{\color{red}{\xi_i}}]\&\qquad -\sum_i \lambda_i{\color{red}{\xi_i}}\large] \&=0+\sum_iC-\sum_{i=1}^n\alpha_i-\sum_i\lambda_i
{\color{red}{\rightarrow0}} \\rightarrow C&=\alpha_i+\lambda_i
\tag{3.6}
\end{align}
\]
代入:将\(3.4,3.5,3.6\)代入拉格朗日函数
\[
\begin{align}
{\cal{L}(w,b,\xi,\alpha,\beta)}
&=
\large[\frac{1}{2}\|W\|^2+\color{red}{C\sum_{i}\xi_i}\&\qquad -\sum_{i=1}^n\alpha_i[y_i(W^{\top}x_i+b)-1+{\color{red}{\xi_i}}]\&\qquad -\sum_i \lambda_i{\color{red}{\xi_i}}\large] \&=
\frac{1}{2}\sum_{i=1}^n\alpha_i\alpha_jy_iy_jx_ix_j+(\alpha_i+\lambda_i)\sum_i{\color{red}{\xi_i}}\&\qquad -\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_jx_ix_j-b\sum_{i=1}^n\alpha_iy_i+
\sum_{i=1}^n\alpha_i (1-{\color{red}{\xi_i}})\&\qquad -\sum_i\lambda_i\color{red}{\xi_i}\&=
-\frac{1}{2}\sum_{i=1}^n\alpha_i\alpha_jy_iy_jx_ix_j-
0+
\sum_{i=1}^n\alpha_i +
0\sum_i\color{red}{\xi_i}\&=
\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\alpha_i\alpha_jy_iy_jx_ix_j
\tag{3.7}
\end{align}
\]
dual问题:
\[
\begin{align}
max_{\alpha}\;W(\alpha)
&=
\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\alpha_i\alpha_jy_iy_jx_ix_j \s.t.\;
&\alpha_i\geq 0\&\sum_{i=1}^n\alpha_iy_i=0 \&{\color{red}{\alpha_i\leq C}}
\end{align}
\]
推导\(b\):(同上)
决策子:(同上)
补充:当前形式的KKT条件(参考\([5]\) -7)
\[
\begin{cases}&\alpha_i&=&0 &\Rightarrow &y_i(W^{\rm{T}}x+b) &\geq 1 \\&\alpha_i&=&C &\Rightarrow &y_i(W^{\rm{T}}x+b)&\leq 1 \\0&<&\alpha_i&<C&\Rightarrow &y_i(W^{\rm{T}}x+b)&= 1 \\\end{cases}
\]
由上可得dual 问题,模型:
\[
\begin{align}
max_{\alpha}\;W(\alpha)
&=
\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\alpha_i\alpha_j
{\color{blue}{y_iy_j}}{\color{green}{x_ix_j}} \s.t.\;
&\alpha_i\geq 0\&\sum_{i=1}^n{\color{orange}{\alpha_iy_i}}=0 \&C\geq \alpha_i
\end{align}
\]
模型中元素(蓝色、绿色、橙色标注):
\[
\begin{align}
max &\begin{cases}
-{\color{blue}{y_iy_j}}:\;
两样本标签同类,值减少 & 阻碍max
\-{\color{green}{x_ix_j}}:\;
两样本数据相似,值减少 & 阻碍max
\-{\color{blue}{y_iy_j}}{\color{green}{x_ix_j}}:\;
两样本内在逻辑类似,值减少 & 阻碍max
\\end{cases}\\sum_{i=1}^n &\begin{cases}
{\color{orange}{\alpha_iy_i}}:\;
不同类标签各自加和,绝对值相等
\\end{cases}\\end{align}
\]
(感觉有点模糊,可能此处反应出SVM模型潜在变量和支持向量的\(\alpha>0\)有关)
(from greedyai.com)
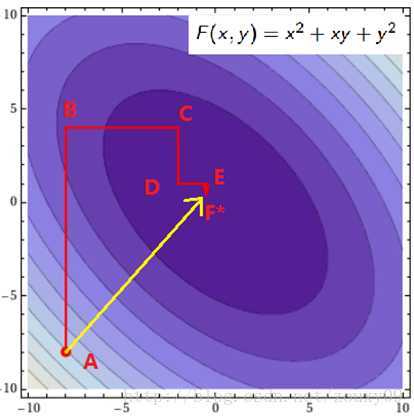
from \([5]\)
迭代公式
for i in range(n):
"""
X: sample data matrix
alpha: Lagrangian multiplier
d: coordinate direction
"""
# i^th sample k^th feature
X[i][k] = X[i-1][k]+alpha[i][k]*d[i][k]
d[i][k] = e[i]收敛依据
\[
\|x_n^k-x_0^k\|\leq \varepsilon
\]
通用流程,无约束优化方法——坐标轮换法,
CS 229, Autumn 2009 - The Simplified SMO Algorithm, SVM-w-SMO,
(SMO是一种坐标下降法\([1]\) )
选择:待固定权重\(\alpha_i,\alpha_j\)(启发式搜索)
判断:判断权重结果,不符合则重新选择
\[
\begin{align}
&k={\cal{K}}(i,i)+{\cal{K}}(j,j)-2{\cal{K}}(i,j) \;
,s.t.\,k>0
\end{align}
\]
更新:合适地更新权重\(\alpha_i,\alpha_j\)
\[
\begin{align}
&\alpha_j^{new}=
\begin{cases}
U & min\\alpha_j^{old}+\frac{y(E_j-E_i)}{k} & \alpha \V & max \\end{cases} \&\alpha_i^{new}=\alpha_i^{old}+y_iy_j(\alpha_j^{old}-\alpha_j^{new})\s.t.&\;U\leq \alpha_j\leq V \&\define&\;\begin{cases}
E_m=\sum_{l=1}^n[\alpha_jy_lK(l,m)]+b-y_m \U=
\begin{cases}
max(0,\alpha_j^{old}-\alpha_i^{old}) &y_i\neq y_j\max(0,\alpha_j^{old}+\alpha_i^{old}-C) &y_i= y_j\\end{cases}\V=
\begin{cases}
min(0,\alpha_j^{old}-\alpha_i^{old})+C &y_i\neq y_j\min(C,\alpha_j^{old}+\alpha_i^{old}) &y_i= y_j\\end{cases}\\end{cases} \\end{align}
\]
更新:合适地更新\(b\)
\[
\begin{align}
b=&(b_x+b_y)/2,\;\;init\;0\b_x&=b-E_{\color{blue}{i}}\&\qquad-y_i(\alpha_i^{new}-\alpha_i^{old}){\cal{K}}(i,{\color{blue}{i}})\&\qquad-y_i(\alpha_j^{new}-\alpha_j^{old}){\cal{K}}({\color{blue}{i}},j),\;\;0<\alpha_{\color{blue}{i}}^{new}<C\b_y&=b-E_{\color{green}{j}}\&\qquad-y_i(\alpha_i^{new}-\alpha_i^{old}){\cal{K}}(i,{\color{green}{j}})\&\qquad-y_i(\alpha_j^{new}-\alpha_j^{old}){\cal{K}}({\color{green}{j}},j),\;\;0<\alpha_{\color{green}{j}}^{new}<C\\\\end{align}
\]
收敛:满足KKT条件
Polynomial Kernel
\[
\begin{align}
&{\cal{K}}(x_i,x_j)=
({\large<}x_i,x_j{\large>}+c)^d \\end{align}
\]
Gaussian Kernel(need:feature standardization)
\[
\begin{align}
&{\cal{K}}(x_i,x_j)=
\exp(-\frac{\|x_i-x_j\|_2^2}{2\sigma^2}) \&\qquad\begin{cases}
lower\;bias&low\;\sigma^2\lower\;variance&high\;\sigma^2\\end{cases}
\end{align}
\]
Sigmoid Kernel(equal:NN without hidden layer)
\[
\begin{align}
&{\cal{K}}(x_i,x_j)=
\tanh(\alpha{\large<}x_i,x_j{\large>}+c) \\end{align}
\]
Cosine Similarity Kernel(used:text similarity)
\[
\begin{align}
&{\cal{K}}(x_i,x_j)=
\frac{{\large<}x_i,x_j{\large>}}
{\|x_i\|\|x_j\|} \\end{align}
\]
Chi-squared Kernel
\[
\begin{align}
SVM:\;&{\cal{K}}(x_i,x_j)=
1-\sum_{i=1}^n{\frac{(x_i-y_i)^2}{0.5(x_i+y_i)}}\rest:\;&{\cal{K}}(x_i,x_j)=
\sum_{i=1}^n{\frac{2x_iy_i}{x_i+y_i}} \\end{align}
\]
直观模型
\[
\begin{align}
&{\color{gray}{max_{\alpha}\;W(\alpha)=
\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\alpha_i\alpha_jy_iy_j}}{\color{red}{x_ix_j}} \&{\color{black}{max_{\alpha}\;W(\alpha)=
\sum_{i=1}^n\alpha_i-\frac{1}{2}\sum_{i=1}^n\alpha_i\alpha_jy_iy_j}}{\color{blue}{\cal{K}(x_i,x_j)}} \&s.t.\;
0\leq \alpha_i\leq C,\;\sum_{i=1}^n\alpha_iy_i=0 \&define:\;
{\cal{K}(x_i,x_j)}=
\large<\varPhi(x_i),\varPhi(x_j)\large>\\end{align}
\]
kernel trick
关于正定核\({\cal{K}_i}\)的函数可以转为关于另一个正定核\({\cal{K}_j}\)的函数
预测:
\[
\begin{align}
{\color{gray}{h(x)}}
&{\color{gray}{=sign(W^{\top}X+b)}} \h(x)
&=sign(W^\top\varPhi(X)+b) \&=sign(\sum_i\alpha_iy_i{\cal{K}}(x_i,x)+b)
\end{align}
\]
高维映射(核空间定义可参看B站-3Blue1Brown-微积分的本质)
\[
\begin{align}
polynomial\;kernel&(c=0,d=2):\&{\cal{K}}(x_i,x_j)=
({\large<}x_i,x_j{\large>}+0)^2\&\qquad\qquad={\large<}\varPhi(x_i),\varPhi(x_j){\large>}\&\begin{cases}
\varPhi(x_i)=[x_{i1}^2,x_{i2}^2,\sqrt{2}x_{i1}x_{i2}] \\varPhi(x_j)=
[x_{j1}^2,x_{j2}^2,\sqrt{2}x_{j1}x_{j2}] \\end{cases}\\end{align}
\]
kernel & basis expansion(compared)
Oxford-Basis Expansion, Regularization, Validation, SNU-Basis expansions and Kernel methods,
类似:使用创建多项式方法创建新特征,都可用于线性分类(线性核),都能升维
不同:feature map不同(\(\varPhi(x)\)),存在非线性核
模型:
\[
\begin{align}
linear\;model:
&y=w{\cdot}\varPhi(x)+\epsilon\basis:
&\begin{cases}
\varPhi(x)=[1,x_1,x_2,x_1x_2,x_1^2,x_2^2], D^dfeatures \define:\;D\,dimension,\;d\,polynomials\\end{cases}\kernel:
&\begin{cases}
\varPhi(x)={\cal{K}}(x_1,x_2)
={\large<}x_1,x_2{\large>},\;2\;features\\varPhi(x)=[1,{\cal{K}}(\mu_i,x)],\mu\,is\,centre,
\;i\,features\\end{cases}\\end{align}
\]
重点推荐\([5][6][10]\):
原文:https://www.cnblogs.com/AndrewWu/p/12405767.html