使用mat函数创建矩阵:matr1 = np.mat("1 2 3;4 5 6;7 8 9")
使用matrix函数创建矩阵:matr2 = np.matrix([[123],[456],[789]])
使用bmat函数合成矩阵:np.bmat("arr1 arr2;arr1 arr2")
In[1]: import numpy as np #导入NumPy库
matr1 = np.mat("1 2 3;4 5 6;7 8 9") #使用分号隔开数据
print(matr1)
Out[1]: [[1 2 3]
[4 5 6]
[7 8 9]]
In[2]: matr2 = np.matrix([[1,2,3],[4,5,6],[7,8,9]])
print()
Out[2]: [[1 2 3]
[4 5 6]
[7 8 9]]
In[3]: arr1 = np.eye(3) #创建数组1
print(arr1)
Out[3]: [[1. 0. 0. ]
[0. 1. 0.]
[0. 0. 1. ]]
In[4]: arr2 = 3 * arr1 #创建数组2
print(arr2)
Out[4]: [[3. 0. 0. ]
[0. 3. 0. ]
[0. 0. 3. ]]
In[5]: np.bmat("arr1 arr2;"arr1 arr2) #创建的矩阵
Out[5]: [[1. 0. 0. 3. 0. 0. ]
[0. 1. 0. 0. 3. 0. ]
[0. 0. 1. 0. 0. 3. ]]
In[6]: matr1 = np.bmat("1 2 3;4 5 6;7 8 9") #创建矩阵
print(matr1)
Out[6]: [[1 2 3]
[4 5 6]
[7 8 9]]
矩阵的运算:
矩阵与数相乘:matrl*3
矩阵相加减:,atr1+-matr2
矩阵相乘:matr1*matr2
矩阵对应元素相乘:np.multiply(matr1,matr2)
矩阵特有属性:
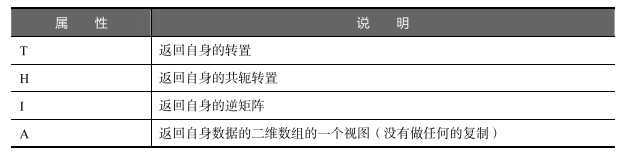
In[6]: matr1 = np.mat("1 2 3;4 5 6;7 8 9") #创建矩阵1
print(matr1)
Out[6]: [[1 2 3]
[4 5 6]
[7 8 9]]
In[7]: matr2 = matr1*3 #创建矩阵2
print(matr2)
Out[7]: [[3 6 9]
[12 15 18]
[21 24 27]]
In[8]: print(matr1+matr2) #矩阵相加
Out[8]: [[4 8 12]
[16 20 24]
[28 32 36]]
In[9]: print(matr1 - matr2) #矩阵相减
Out[9]: [[-2 -4 -6]
[-8 -10 -12]
[-14 -16 -18]]
In[10]: print(matr1 * matr2) #矩阵相乘
Out[10]: [[90 108 126]
[198 243 288]
[306 378 450]]
In[11]: print(np.multiply(matr1,matr2))
Out[11]: [[3 12 27]
[48 75 108]
[147 192 243]]
In[12]: print(matr1.T) #转置
Out[12]: [[1 4 7]
[2 5 8]
[3 6 9]]
In[13]: print(matr1.H) #共轭转置(实数的共轭就是其本身)
Out[13]: [[1 4 7]
[2 5 8]
[3 6 9]]
In[14]: print(matr1.I) #逆矩阵
Out[14]: [[-4.50359963e+15 9.00719925e+15 -4.05359963e+15]
[9.00719925e+15 -1.80143985e+16 9.00719925e+15]
[-4.50359963e+15 9.00719925e+15 -4.50359963e+15]]
In[15]: print(matr1.A) #返回二维数组的视图
Out[15]: [[1 2 3]
[4 5 6]
[7 8 9]]
全称通用函数,是一种能够对数组中所有元素进行操作的函数。
四则运算:加(+)、减(-)、乘(*)、除(/)、幂(**)。数组间的四则运算表示对每个数组中的元素分别进行四则运算,所以形状必须相同。
比较运算:>、<、==、<=、!=。比较运算返回的结果是一个布尔数组,每个元素为每个数组对应元素的比较结果。
逻辑运算:np.any函数表示逻辑"or",np.all函数表示逻辑"and"。运算结果返回布尔值。
In[16]: x = np.array[1,2,3]
y = np.array[4,5,6]
print(x + y) #数组相加
Out[16]: [5 7 9]
In[17]: print(x - y) #数组相减
Out[17]: [-3 -3 -3]
In[18]: print(x * y) #数组相乘
Out[18]: [4 10 18]
In[19]: print(x / y) #数组相除
Out[19]: [0.25 0.4 0.5]
In[20]: print(x ** y) #数组幂运算
Out[20]: [1 32 729]
数组的比较运算:
In[21]: x = np.array([1,3,5])
y = np.array([2,3,4])
print(x < y)
Out[21]: [True False False]
In[22]: print(x > y)
Out[22]: [False False True]
In[23]: print(x == y)
Out[23]: [False True False]
In[24]: print(x >= y)
Out[24]: [False True True]
In[25]: print(x <= y)
Out[25]: [True True False]
In[26]: print(x != y)
Out[26]: [True False True]
In[27]: print(np.all(x == y)) #np.all( )表示逻辑and
Out[27]: False
In[28]: print(np.any(x == y)) #np.any( )表示逻辑or
Out[28]: True
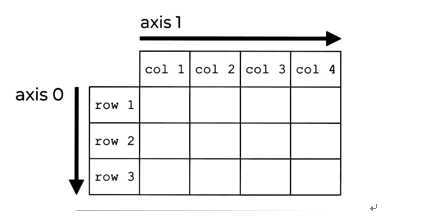
ufunc函数的广播机制:
广播是指不同形状的数组之间执行算数运算的方式。需要遵循4个原则。
* 让所有输入数组都向其中shape最长的数组看齐,shape中不足的部分都通过在前面加1补齐。
* 输出数组的shape是输入数组shape的各个轴上的最大值。
* 如果输入数组的某个轴和输出数组的对应轴的长度相同或者其长度为1时,这个数组能够用来计算,否则出错。
* 当输入数组的某个轴的长度为1时,沿着此轴运算时都用此轴上的第一组值。
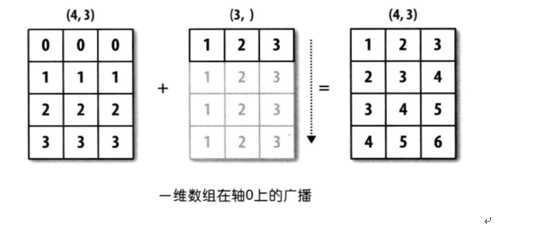
一维数组的广播机制:
In[29]: arr1 = np.array([[0,0,0],[1,1,1],[2,2,2],[3,3,3]])
print(arr1)
Out[29]: [[0 0 0]
[1 1 1]
[2 2 2]
[3 3 3]]
In[30]: print(arr1.shape)
Out[30]: (4, 3)
In[31]: arr2 = np.array([1,2,3])
print(arr2)
Out[31]: [1 2 3]
In[32]: print(arr2.shape)
Out[32]: (3,)
In[33]: print(arr1 + arr2)
Out[33]: [[1 2 3]
[2 3 4]
[3 4 5]
[4 5 6]]
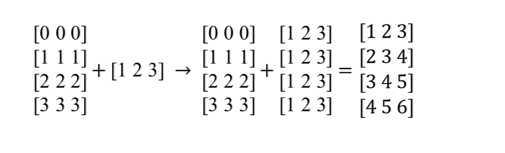
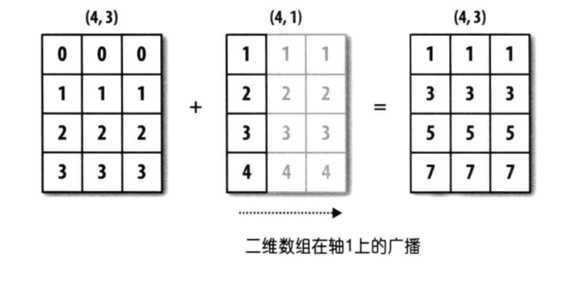
二维数组的广播机制:
In[34]: arr1 = np.array([0,0,0],[1,1,1],[2,2,2],[3,3,3])
print(arr1)
Out[34]: [[0 0 0]
[1 1 1]
[2 2 2]
[3 3 3]]
In[35]: print(arr1.shape)
Out[35]: (4,3)
In[36]: arr2 = np.array([1,2,3,4]).reshape((4,1))
print(arr2)
Out[36]: [[1]
[2]
[3]
[4]]
In[37]: print(arr2.shape)
Out[37]: (4, 1)
In[38]: print(arr1 + arr2)
Out[38]: [[1 1 1]
[3 3 3]
[5 5 5]
[7 7 7]]
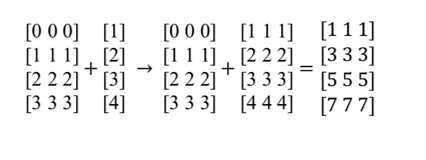
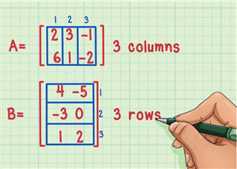
1、确认矩阵是否可以相乘。只有第一个矩阵的列的个数等于第二个矩阵的行的个数,这样的两个矩阵才能相乘。图示的两个矩阵可以相乘,因为第一个矩阵,矩阵A有3列,而第二个矩阵,矩阵B有3行。
2、计算结果矩阵的行列数。画一个空白的矩阵,来代表矩阵乘法的结果。矩阵A和矩阵B相乘得到的矩阵,与矩阵A有相同的行数,与矩阵B有相同的列数。
矩阵A有2行,所以结果矩阵也有2行。矩阵B有2列,所以结果矩阵也有2列。最终的结果矩阵就有2行2列。
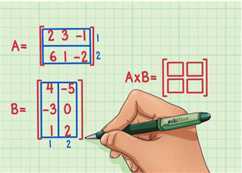
3、计算第一个“点”。要计算矩阵中的第一个“点”,你需要用第一个矩阵第一行的第一个数乘以第二个矩阵第一列的第一个数,第一行的第二个数乘以第一列的第二个数,第一行的第三个数乘以第一列的第三个数,然后将这三个结果加到一起,得到第一个点。先来计算一下结果矩阵中第二行第二列的数,下面是算法:
6 x -5 = -30
1 x 0 = 0
2 x 2 = -4
-30 + 0 + (-4) = -34
结果是-34,对应了矩阵最右下角的位置。
在你计算矩阵乘法时,结果所处的行列位置要满足,行和第一个矩阵的行相同,列和第二个矩阵的列相同。比如,你用矩阵A最下面一行的数乘以矩阵B最右一列的数,得到的结果是-34,所以-34应该是结果矩阵中最右下角的一个数。
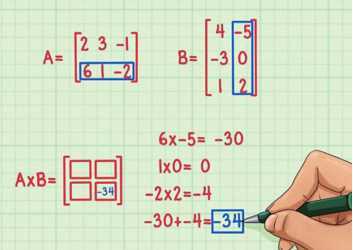
4、计算第二个“点”。比如计算最左下角的数,你需要用第一个矩阵最下面一行的数乘以第二个矩阵最左列的数,然后再把结果相加。具体计算方法和上面一样。
6 x 4 = 24
1 x (-3) = -3
(-2) x 1 = -2
24 + (-3) + (-2) = 19
结果是-19,对应矩阵左下角的位置。

5、在计算剩下的两个“点”。要计算左上角的数,用矩阵A的最上面一行的数乘以矩阵B左侧一列的数,下面是具体算法:
2 x 4 = 8
3 x (-3) = -9
(-1) x 1 = -1
8 + (-9) + (-1) = -2
结果是-2,对应的位置是左上角。
要计算右上角的数,用矩阵A的最上面一行的数乘以矩阵B右侧一列的数,下面是具体算法:
2 x (-5) = -10
3 x 0 = 0
(-1) x 2 = -2
-10 + 0 + (-2) = -12
结果是-12,对应的位置是右上角。
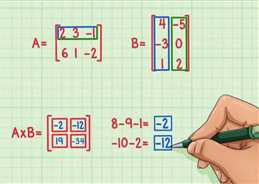
6、检查相应的数字是否出现在正确的位置。19在左下角,-34在右-2在左上角,-12在右上角。

------------恢复内容开始------------
使用mat函数创建矩阵:matr1 = np.mat("1 2 3;4 5 6;7 8 9")
使用matrix函数创建矩阵:matr2 = np.matrix([[123],[456],[789]])
使用bmat函数合成矩阵:np.bmat("arr1 arr2;arr1 arr2")
In[1]: import numpy as np #导入NumPy库
matr1 = np.mat("1 2 3;4 5 6;7 8 9") #使用分号隔开数据
print(matr1)
Out[1]: [[1 2 3]
[4 5 6]
[7 8 9]]
In[2]: matr2 = np.matrix([[1,2,3],[4,5,6],[7,8,9]])
print()
Out[2]: [[1 2 3]
[4 5 6]
[7 8 9]]
In[3]: arr1 = np.eye(3) #创建数组1
print(arr1)
Out[3]: [[1. 0. 0. ]
[0. 1. 0.]
[0. 0. 1. ]]
In[4]: arr2 = 3 * arr1 #创建数组2
print(arr2)
Out[4]: [[3. 0. 0. ]
[0. 3. 0. ]
[0. 0. 3. ]]
In[5]: np.bmat("arr1 arr2;"arr1 arr2) #创建的矩阵
Out[5]: [[1. 0. 0. 3. 0. 0. ]
[0. 1. 0. 0. 3. 0. ]
[0. 0. 1. 0. 0. 3. ]]
In[6]: matr1 = np.bmat("1 2 3;4 5 6;7 8 9") #创建矩阵
print(matr1)
Out[6]: [[1 2 3]
[4 5 6]
[7 8 9]]
矩阵的运算:
矩阵与数相乘:matrl*3
矩阵相加减:,atr1+-matr2
矩阵相乘:matr1*matr2
矩阵对应元素相乘:np.multiply(matr1,matr2)
矩阵特有属性:

In[6]: matr1 = np.mat("1 2 3;4 5 6;7 8 9") #创建矩阵1
print(matr1)
Out[6]: [[1 2 3]
[4 5 6]
[7 8 9]]
In[7]: matr2 = matr1*3 #创建矩阵2
print(matr2)
Out[7]: [[3 6 9]
[12 15 18]
[21 24 27]]
In[8]: print(matr1+matr2) #矩阵相加
Out[8]: [[4 8 12]
[16 20 24]
[28 32 36]]
In[9]: print(matr1 - matr2) #矩阵相减
Out[9]: [[-2 -4 -6]
[-8 -10 -12]
[-14 -16 -18]]
In[10]: print(matr1 * matr2) #矩阵相乘
Out[10]: [[90 108 126]
[198 243 288]
[306 378 450]]
In[11]: print(np.multiply(matr1,matr2))
Out[11]: [[3 12 27]
[48 75 108]
[147 192 243]]
In[12]: print(matr1.T) #转置
Out[12]: [[1 4 7]
[2 5 8]
[3 6 9]]
In[13]: print(matr1.H) #共轭转置(实数的共轭就是其本身)
Out[13]: [[1 4 7]
[2 5 8]
[3 6 9]]
In[14]: print(matr1.I) #逆矩阵
Out[14]: [[-4.50359963e+15 9.00719925e+15 -4.05359963e+15]
[9.00719925e+15 -1.80143985e+16 9.00719925e+15]
[-4.50359963e+15 9.00719925e+15 -4.50359963e+15]]
In[15]: print(matr1.A) #返回二维数组的视图
Out[15]: [[1 2 3]
[4 5 6]
[7 8 9]]
全称通用函数,是一种能够对数组中所有元素进行操作的函数。
四则运算:加(+)、减(-)、乘(*)、除(/)、幂(**)。数组间的四则运算表示对每个数组中的元素分别进行四则运算,所以形状必须相同。
比较运算:>、<、==、<=、!=。比较运算返回的结果是一个布尔数组,每个元素为每个数组对应元素的比较结果。
逻辑运算:np.any函数表示逻辑"or",np.all函数表示逻辑"and"。运算结果返回布尔值。
In[16]: x = np.array[1,2,3]
y = np.array[4,5,6]
print(x + y) #数组相加
Out[16]: [5 7 9]
In[17]: print(x - y) #数组相减
Out[17]: [-3 -3 -3]
In[18]: print(x * y) #数组相乘
Out[18]: [4 10 18]
In[19]: print(x / y) #数组相除
Out[19]: [0.25 0.4 0.5]
In[20]: print(x ** y) #数组幂运算
Out[20]: [1 32 729]
数组的比较运算:
In[21]: x = np.array([1,3,5])
y = np.array([2,3,4])
print(x < y)
Out[21]: [True False False]
In[22]: print(x > y)
Out[22]: [False False True]
In[23]: print(x == y)
Out[23]: [False True False]
In[24]: print(x >= y)
Out[24]: [False True True]
In[25]: print(x <= y)
Out[25]: [True True False]
In[26]: print(x != y)
Out[26]: [True False True]
In[27]: print(np.all(x == y)) #np.all( )表示逻辑and
Out[27]: False
In[28]: print(np.any(x == y)) #np.any( )表示逻辑or
Out[28]: True
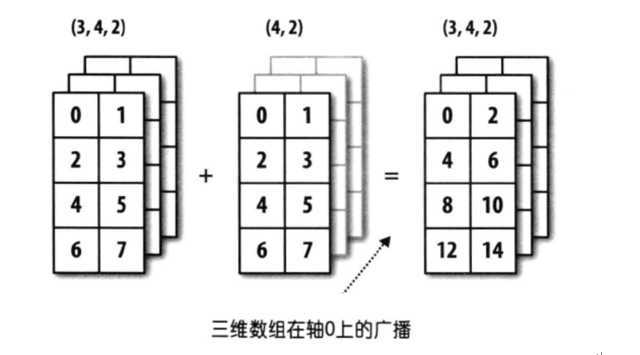
ufunc函数的广播机制:
广播是指不同形状的数组之间执行算数运算的方式。需要遵循4个原则。
* 让所有输入数组都向其中shape最长的数组看齐,shape中不足的部分都通过在前面加1补齐。
* 输出数组的shape是输入数组shape的各个轴上的最大值。
* 如果输入数组的某个轴和输出数组的对应轴的长度相同或者其长度为1时,这个数组能够用来计算,否则出错。
* 当输入数组的某个轴的长度为1时,沿着此轴运算时都用此轴上的第一组值。
一维数组的广播机制:
In[29]: arr1 = np.array([[0,0,0],[1,1,1],[2,2,2],[3,3,3]])
print(arr1)
Out[29]: [[0 0 0]
[1 1 1]
[2 2 2]
[3 3 3]]
In[30]: print(arr1.shape)
Out[30]: (4, 3)
In[31]: arr2 = np.array([1,2,3])
print(arr2)
Out[31]: [1 2 3]
In[32]: print(arr2.shape)
Out[32]: (3,)
In[33]: print(arr1 + arr2)
Out[33]: [[1 2 3]
[2 3 4]
[3 4 5]
[4 5 6]]
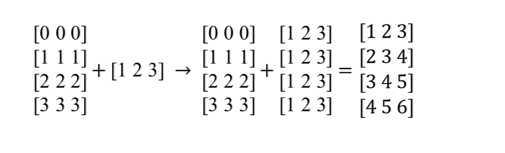

二维数组的广播机制:
In[34]: arr1 = np.array([0,0,0],[1,1,1],[2,2,2],[3,3,3])
print(arr1)
Out[34]: [[0 0 0]
[1 1 1]
[2 2 2]
[3 3 3]]
In[35]: print(arr1.shape)
Out[35]: (4,3)
In[36]: arr2 = np.array([1,2,3,4]).reshape((4,1))
print(arr2)
Out[36]: [[1]
[2]
[3]
[4]]
In[37]: print(arr2.shape)
Out[37]: (4, 1)
In[38]: print(arr1 + arr2)
Out[38]: [[1 1 1]
[3 3 3]
[5 5 5]
[7 7 7]]
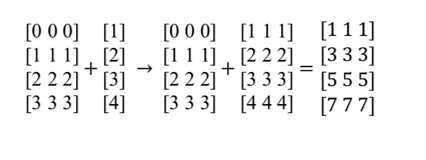



1、确认矩阵是否可以相乘。只有第一个矩阵的列的个数等于第二个矩阵的行的个数,这样的两个矩阵才能相乘。图示的两个矩阵可以相乘,因为第一个矩阵,矩阵A有3列,而第二个矩阵,矩阵B有3行。

2、计算结果矩阵的行列数。画一个空白的矩阵,来代表矩阵乘法的结果。矩阵A和矩阵B相乘得到的矩阵,与矩阵A有相同的行数,与矩阵B有相同的列数。
矩阵A有2行,所以结果矩阵也有2行。矩阵B有2列,所以结果矩阵也有2列。最终的结果矩阵就有2行2列。

3、计算第一个“点”。要计算矩阵中的第一个“点”,你需要用第一个矩阵第一行的第一个数乘以第二个矩阵第一列的第一个数,第一行的第二个数乘以第一列的第二个数,第一行的第三个数乘以第一列的第三个数,然后将这三个结果加到一起,得到第一个点。先来计算一下结果矩阵中第二行第二列的数,下面是算法:
6 x -5 = -30
1 x 0 = 0
2 x 2 = -4
-30 + 0 + (-4) = -34
结果是-34,对应了矩阵最右下角的位置。
在你计算矩阵乘法时,结果所处的行列位置要满足,行和第一个矩阵的行相同,列和第二个矩阵的列相同。比如,你用矩阵A最下面一行的数乘以矩阵B最右一列的数,得到的结果是-34,所以-34应该是结果矩阵中最右下角的一个数。
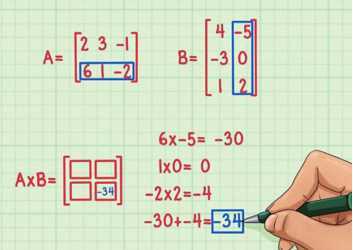
4、计算第二个“点”。比如计算最左下角的数,你需要用第一个矩阵最下面一行的数乘以第二个矩阵最左列的数,然后再把结果相加。具体计算方法和上面一样。
6 x 4 = 24
1 x (-3) = -3
(-2) x 1 = -2
24 + (-3) + (-2) = 19
结果是-19,对应矩阵左下角的位置。

5、在计算剩下的两个“点”。要计算左上角的数,用矩阵A的最上面一行的数乘以矩阵B左侧一列的数,下面是具体算法:
2 x 4 = 8
3 x (-3) = -9
(-1) x 1 = -1
8 + (-9) + (-1) = -2
结果是-2,对应的位置是左上角。
要计算右上角的数,用矩阵A的最上面一行的数乘以矩阵B右侧一列的数,下面是具体算法:
2 x (-5) = -10
3 x 0 = 0
(-1) x 2 = -2
-10 + 0 + (-2) = -12
结果是-12,对应的位置是右上角。

6、检查相应的数字是否出现在正确的位置。19在左下角,-34在右-2在左上角,-12在右上角。
原文:https://www.cnblogs.com/XiaMengJie/p/12431405.html