一、 算法入门

博主在市面上发现了很多，很多有关书算法的书籍，但是真正能够让初学者易懂的算法书籍，只是一点点，以下我讲以
Aditya Bhargava写的一本关于算法的入门书籍，为参考，这本书非常的优秀，浅显易懂，图文并茂！带你走进算法的世界，要知道，作为一名优秀的程序员，不会算法是不行滴。
书籍的地址，可以给博主留言，也可以加我QQ或者微信，欢迎你和我一起来探讨，编程世界的秘密

二、 算法简介

所谓的算法是一组完成任务的指令，这个任务可以是有关数学的，也可以是有关功能的实现，

算法是计算机的灵魂

• 我们学习算法可以干些什么呢？

具体说来，我们可以实现编写跟着用户的AI系统，编写推荐系统，当然了还有NP的一些问题。不过呢，准备好掉头发了吗？让我们一起来掉头发吧！！

第一个算法——二分查找

所谓的二分查找算法，是一个非常简单的入门算法，它的目的是加快数据的查找

1.让我们从需求出发

• 我这里现在有1~10的数子，我现在随机说一个数组，你去猜。我们基本上可以使用两种方法

1. 一个一个的去猜，假如我说的1那么恭喜你，你一下子就猜到了。要是我说的是10？那你可能要猜10次
2. 使用二分查找法，假如我说的1那么你可以猜5，我说”不对，大了“,那你又说”2”，我说“不对，大了”，如何你又猜到1，我说 “猜对了“这时候，你只需要猜3次就猜到了

• 在大量的数学论证中，我们可以用数学公式对二分查找所需要的最大次数，得出这样的一个公式

\[ x=log_2 N,2^3=8，log_28=3,log_22^3=3 \]
它指的是如果你在n个要查找的元素中，需要找一个元素，那么你最多需要x步。

• 注意如果你连上述的公式都看不懂，那么我也许会怀疑你的高数是不是体育老师教的了。
• 需要提醒你的是，这n个元素要有顺序！，也就是说 如果是一个无序的组合，那么这个算法行不通

2. 如何用代码表示呢?（Python）

特别需要你注意的是：我们这选用python做为编程语言，python简单易学

博主比较忙，简单的代码就不敲了，复杂一些的会带着大家敲一下

三、对于算法的效率

1. 通过前面的学习，我们可能绝对这个二分查找好像并没有多块啊，但是如果你要查找40亿个数据，使用二分查找你只需要35次

\[ log_240(亿)= 35 \]
\[ log_2100 \approx7 \]

1. 那么我们如何用另一种算法来表示，它运算的时间呢？

   难不倒我们伟大的程序员，这里哟一种叫做大O表示法，一张图告诉你
   

2. 我们可以这样子去理解，所谓的大O表示法，其实是 从算法运算的时间增量的角度来衡量的，它没有单位

例子1：比如下面的例子，有助于你的理解，

假设还是二分查找和普通的算法，查找一次需要用到1毫秒ms，从n个中找一个元素，n=100时，普通算法需要的时间是100ms，而二分查找需要的时间约等于7ms,当n=1000时，普通算法是10s，二分查找需要耗费14ms，

有此我们可以使用以下的公式来表示，它们运行的速度

\[ 普通算法：O_(n), \]
\[ 二分算法：O_(log_2n) \]

我们这里的（）括号里的数表示的操作数，表示执行这个算法需要操作多少步，或者说操作多少次。

例子2：现在有一个需求，在一张纸上面绘制16个各种，那么如何用大O表示法，来观察它的运行速度呢？

算法1：一个一个的去画，你需要画16次，
算法2：二分的去画，只需要画4次，这个4怎么得来的呢？我们能不能用数学表示出来呢？当然可以，看我们的公式

\[ log_216=4 \]

所以在例子二中，算法1，2用大O表示法就是

\[ 普通算法：O_(n), \]
\[ 二分算法：O_(log_2n) \]

再说一遍，我们的运行速度指是运算的时间的增量

1.我这里指出了参加的大O运行时间

再来一个简单的例子：
还是要绘制16个各种，如果现在要求绘制的1024的格子呢？我们如何用以上的5种表示法表示出来？

• 实际上，不可能如此干净的把大O运行时间转化为操作数，就目前来看，这种情况下的精度就够了，后面我们再来深入的套路大O表示法

2.总结一下

四.有趣的问题（旅行商的问题）

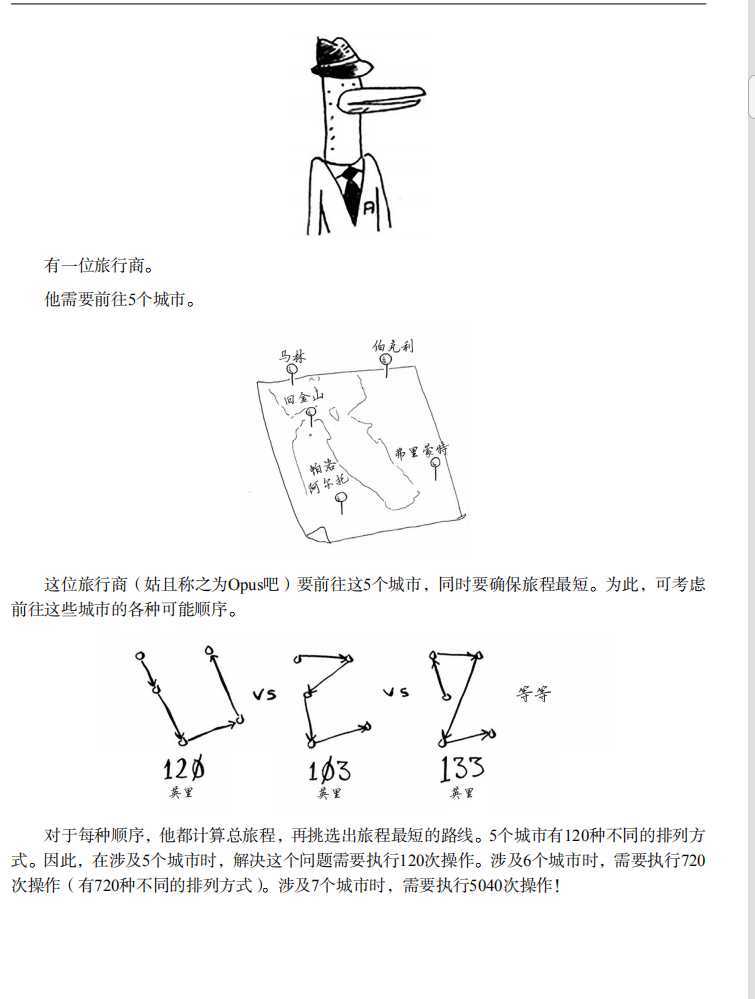
这是一个著名的计算机科学领域的问题，它充分的表示了最后一种大O表示法的运行速度

五、总结

• 二分查找的速度要快于简单查找

\[ 普通算法：O_(n),比较慢，而且元素越多越慢 \]
\[ 二分算法：O_(log_2n) \]

• 算法的运行时间不是s为单位，而是以其运算的增速角度来度量的
• 运算时间可以用大O来表示

算法入门——二分查找，旅行商问题，大O表示法

原文：https://www.cnblogs.com/BM-laoli/p/12431467.html