以下的排序都以按数值大小升序为最终的排序目标
非常暴力且直接的思路,每个元素两两比较,直到所有元素都放在了正确的位置。
实际上达到的效果是每一趟循环都把一个当前最小的元素(或最大的元素)放到了正确位置。
for (int i = 0; i < n; ++i) {
for (int j = n - 1; j >= i; --j) {
if (arr[j] < arr[j - 1]) {
swap(arr[j], arr[j - 1]);
}
}
}j从0 -> n - i则是每一趟把最大的元素放在了最后;j从n-1 -> i则是每一趟把最小的元素放在了最前。无论哪种,序列的待排序的片段总是每次长度-1,即每一次的有序子段总是长度+1.
可以发现冒泡排序是对未排完序的部分序列进行的完整遍历,每一次遍历也可以看作是对剩余片段的一次检查,所以可以使用一个变量flag来标识此趟遍历是否进行过了交换,若没有,则说明序列当前已经有序,已经可以结束算法了。
for (int i = 0; i < n; ++i) {
bool flag = false;
for (int j = 1; j < n - i; ++j) {
if (arr[j] < arr[j - 1]) {
swap(arr[i], arr[j]);
flag = true;
}
}
if (!flag) break; // 已经有序,结束算法
}暴力遍历\(O(n^2)\)
跟冒泡排序非常相似,只不过其思路更加直观:每次选择未排好序中的最小值,添加到已经排好序的子序列。实际上可以看作是延迟交换的冒泡排序。
这里已经排好序的子序列,其实就是逻辑上已经排好序的前缀,初始长度为0。(当然每次将最大的元素放到后缀也是一样的)
// tail 为已经排好序前缀的下一个位置下标
// low_index 用于记录最小值的下标
for (int tail = 0; tail < n; ++tail) {
int low_index = tail;
for (int j = tail + 1; j < n; ++j) {
if (arr[j] < arr[low_index]) low_index = j;
}
swap(arr[low_index], arr[tail]);
}\(n \rightarrow 1\) 长度等差序列求和,复杂度\(O(n^2)\)。
插入排序是一种由子结构逐渐构造的思路,假设序列(L)有序,那么插入一个新的元素到正确位置后,(L+1)仍然有序。
我们将原序列逻辑上分成两个部分,一个部分是有序前缀(初始长度为0),一个是无序后缀(初始就是序列本身)。逐个拓展前缀,每次新的入列元素与前面已排序的子序列进行比较,将新的记录插入到有序子序列中的正确位置,此消彼长直至前缀的长度为原序列的长度。
// len 前缀末尾的下一个位置,初始为1或0都一样
// 每一次len的增加就相当于添加了一个新的元素,将其放到正确位置即可
for (int len = 1; len < n; ++len) {
for (int i = len; i > 0 && arr[i] < arr[i - 1]; --i)
// 已经排好序的子序列为0~i-1,i是最新进来的元素,给其找一个正确的位置
// 找到正确的位置即可停止交换,即当arr[j]已经<=arr[j-1]时
swap(arr[i], arr[i - 1]);
}也是等差数列求和,复杂度\(O(n^2)\)。
希尔排序是排序史上对\(O(n^2)\)的一次突破,基本动机是利用,在序列基本有序的前提下,插入排序的时间效率可以提高到\(Θ(n)\).它是插入排序的升级版。
思路是:按照一定的增量,将原序列分组,对每组进行插入排序,随着增量逐渐减少,分组的序列越来越长。当增量减为1时,就是对已经基本有序的数组进行插入排序。
// 最直观的版本
for (int incr = n / 2; incr > 0; incr /= 2) {
for (int i = 0; i < incr; ++i) { // 每组的首元素
// 组内插入排序
for (int j = i + incr; j < n; j += incr)
for (int k = j; k > i && arr[k] < arr[k - incr]; k -= incr)
swap(arr[k], arr[k - incr]);
}
}
// 改进版本
// 不是每一次都针对某个组进行插入排序
// 而是在遍历的时候遇到哪个组,就对哪个组进行插入排序
for (int incr = n / 2; incr > 0; incr /= 2) { // 增量
for (int i = incr; i < n; ++i) {
for (int j = i; j >= incr && arr[j] < arr[j - incr]; j -= incr)
swap(arr[j], arr[j - incr]);
}
}emm,这个就很难说了,跟你的增量序列选取有关,平均是\(Θ(n^{1.5})\)。
学排序若你不会快排就白学了~这个是一个非常伟大的排序算法。
比起之前的暴力遍历,快速排序采用了分治的思想,是一种划分交换排序。
基本思路是每次找一个轴值
pivot,用划分算法将剩余序列分为两部分,比pivot大的放在后部分,小的放在前部分,接着分别对前后两部分继续用上述思路确定pivot直至部分的长度为1
// @return 轴值在序列中的正确位置
// l r 要划分的闭区间界限
int partition(int arr[], int l, int r, int pivot_index) {
int pivot = arr[pivot_index];
int low = l-1;
for (int i = l; i <= r; ++i) {
if (arr[i] < pivot) {
swap(arr[++low], arr[i]);
}
}
return low + 1;
}
// 这个版本的划分是许多教科书上的
// 个人觉得没那么好理解,能简化的东西就简化吧
int partition(int arr[], int l, int r, int pivot_index) {
int pivot = arr[pivot_index];
int low = l, high = r;
while (low <= high) {
while(arr[low] < pivot) ++low;
while(low < high && arr[high] > pivot) --high;
swap(arr[low], arr[high]);
}
return low;
}
// l 和 r 是闭区间界限
void quick_sort(int arr[], int l, int r) {
if (l < r) {
int pivot = arr[l];
swap(arr[l], arr[r]); // 将轴值放到最后,对剩余序列及逆行划分
int k = partition(arr, l, r - 1, r);
swap(arr[k], arr[r]);
quick_sort(arr, l, k - 1);
quick_sort(arr, k + 1, r);
}
}最优情况下:每次划分均匀,那么递归树应该是比较平衡的,可以领用递归的方式计算
\[
T(n) = 2T(n/2) + n \\T(n) = 2(2T(n/4) + n) + n \\\rightarrow T(n) = 2^{logn} + nlogn = n + logn\\\rightarrow O(logn)
\]
最糟糕的情况下:递归树是一颗斜树,那么比较次数就是等差数列求和了,复杂度\(O(n^2)\)。
平均情况下\(O(nlogn)\)。
也是一种基于比较的分治排序法,这里仅介绍简单的二路归并。将两个有序的序列合并成一个有序的序列是非常简便的,归并排序就利用了这种想法。
基本思路:(1) 长度为n的待排序序列,分为n个有序子序列,长度为1就必然是有序嘛~ (2) 两两归并子序列,获得若干个长度更长的有序序列 (3) 重复第2步直至序列归一
从递归树的角度看,归并排序的信息是从叶子开始逐渐自底向上传递
void merge_sort(int arr[], int l, int r, int tmp[]) {
if (l >= r) return; // 只有一个元素(基例)
int mid = (l + r) >> 1; // 地板除2,划分序列
merge_sort(arr, l, mid); // 先继续向下完善信息,之后才能够自底向上传递信息
merge_sort(arr, mid+1, r);
// merge
for (int i = l; i <= r; ++i) {
tmp[i] = arr[i];
}
int i1 = l, i2 = mid + 1;
for (int c = l; c <= r; ++c) {
if (i1 > mid) arr[c] = tmp[i2++];
else if (i2 > r) arr[c] = tmp[i1++];
else arr[c] = tmp[i1] < tmp[i2] ? tmp[i1++] : tmp[i2++];
}
}分析过程和快排类似,时间复杂度\(O(nlogn)\)。但是由于每次都是均匀划分,所以递归树不会出现像快排那样的斜树情况,故归并排序算法的复杂度是比较稳定的。
这种排序简直是精彩!利用了堆这个漂亮的数据结构!
堆是一个层层部分有序的完全二叉树,所以最优的存储方式就是数组,完美切合了我们的序列,所以只需要:
将要排序的序列构建成最大值堆,之后逐个删除堆顶元素(所谓的删,是逻辑删,其实是将堆顶移到了最后的叶子节点),就可以获得一个升序序列了。
void shift_down(int arr[], int t, int n) {
while (t < n) {
int lef = (t<<1) + 1, rig = lef + 1;
if (rig < n && arr[lef] < arr[rig]) // 方便之后统一与lef指针交换
lef = rig;
if (lef < n && arr[t] < arr[lef]) {
swap(arr[t], arr[lef]);
t = lef;
} else break;
}
}
// 交换建堆法,构建最大值堆
// 从第一个非叶子节点开始,进行下拉操作
// 如何找到第一个非叶子节点呢?
// 节点i,左孩子(2*i+1),右孩子(2*i+2),若左孩子存在就是非叶子了
// 也可以这么看,最后一个叶子(n-1)的爸爸就是第一个非叶子节点 => (n-2) / 2
void make_heap(int arr[], int n) {
for (int i = (n-2) >> 1 ; i >= 0; --i) {
shift_down(arr, i, n);
}
}
void pop_heap(int arr[], int n) {
// 删除
swap(arr[0], arr[n - 1]);
// 维护
shift_down(arr, 0, n - 1);
}
void heap_sort(int arr[], int n) {
make_heap(arr, n);
for (int i = n; i > 1; --i) {
pop_heap(arr, i);
}
}交换建堆\(O(n)\),n次删除\(O(nlogn)\)。所以复杂度为\(O(nlogn)\)。
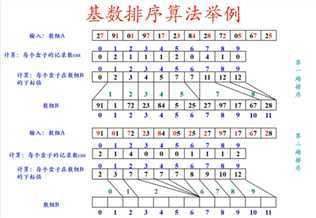
哇,个人觉得这种排序的思路能想出来真的是神仙~感觉有些颠覆之前的值比较算法,我们在比较两个数的时候,除了最直接的值比较,还可以由最低位开始到高位,一旦出现了某个位数数值的不同,两数的大小就已分高下。基数排序就是利用了这种思路。
所谓基数(Radix)就是指数的进制,基本思路:
将所有待排序的数值(正整数)按照基数r,统一为一样长度的数(不够长可以前边补0),然后从最低位开始依次进行数值的计数排序。
// A[] 待排序数组
// B[] 用于装载结果
// n 数组元素个数
// k 数字的位数
void radix_sort(int A[], int B[], int n, int k, int r, int cnt[]) {
int j;
// rtok 用于辅助获取某一位
for (int i = 0, rtok=1; i < k; ++i, rtok *= r) {
memset(cnt, 0, sizeof(cnt));
// cnt 数组记录当前位数的0-r出现个数
// 之后利用前缀和,计算出0-r每个数在B数组中位置的**后界限**
for (j = 0; j < n; ++j) cnt[ (A[i]/rtok) % r ] += 1;
for (j = 1; j < r; ++j) cnt[j] = cnt[j - 1] + cnt[j];
for (j = n - 1; j >= 0; --j)
B[ --cnt[ (A[j]/rtok) % r ] ] = A[j];
for (j = 0; j < n; ++j)
A[j] = B[j]; // 更新完的结果拷贝回A[]
}
}
\(O(nk + rk)\)
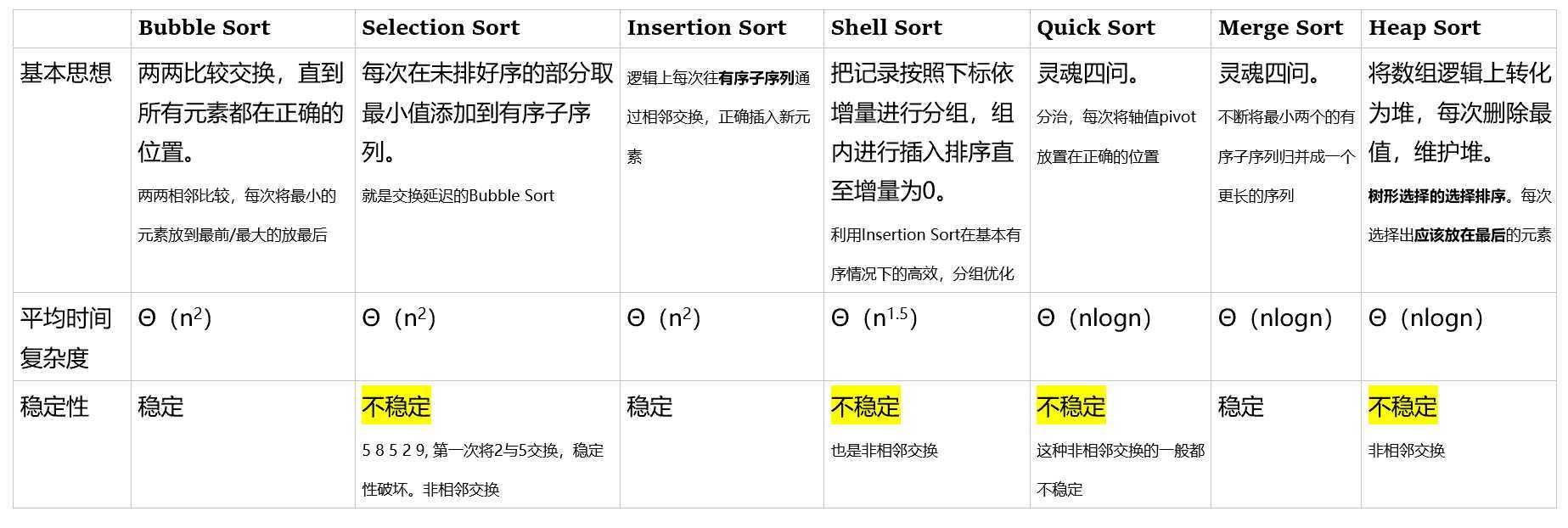
附上笔者自己总结的一张表吧
原文:https://www.cnblogs.com/GorgeousBankarian/p/12458121.html