
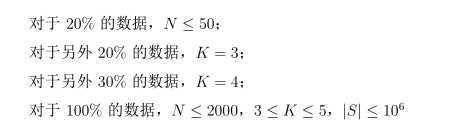
考虑用总数-不合法数
因为相同情况只有轮换和翻转,所以总数=\(n^{\underline{K}}/2K\)
K=3时,不合法的情况只有三元组的一个点有两条向外的边,并且每个三元组中只有一个这样的点,统计一下即可
K=4时减只有一个向外的加有两个向外的,K=5同理,只不过两个向外的点连了一个共同点,两个不同点
bitset即可做到O(n^3/ω),需要预处理每个点的出度
注意细节
#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define ll long long
#define file
using namespace std;
bitset<2001> a[2001],A;
int m,i,j,k,l,x,y;
char st[1000001];
ll c[2001],n,ans,s,s1,s2;
void nxt()
{
if (y<n) ++y;
else ++x,y=x+1;
}
int main()
{
freopen("deathstar.in","r",stdin);
#ifdef file
freopen("deathstar.out","w",stdout);
#endif
scanf("%lld%d",&n,&m);
scanf("%s",st);l=strlen(st);
x=1;y=2;
fo(i,0,l-1)
{
if (st[i]>='0' && st[i]<='9')
j=st[i]-'0';
else
j=st[i]-'A'+10;
if (j&8) a[x][y]=1,++c[x]; else a[y][x]=1,++c[y]; nxt(); if (x==n) break;
if (j&4) a[x][y]=1,++c[x]; else a[y][x]=1,++c[y]; nxt(); if (x==n) break;
if (j&2) a[x][y]=1,++c[x]; else a[y][x]=1,++c[y]; nxt(); if (x==n) break;
if (j&1) a[x][y]=1,++c[x]; else a[y][x]=1,++c[y]; nxt(); if (x==n) break;
}
switch (m)
{
case 3:{
ans=n*(n-1)*(n-2)/6;
fo(i,1,n)
{
s=c[i];
ans-=s*(s-1)/2;
}
break;
}
case 4:{
ans=n*(n-1)*(n-2)*(n-3)/8;
fo(i,1,n)
{
s=c[i];
ans-=s*(s-1)/2*(n-3);
}
fo(i,1,n-1)
{
fo(j,i+1,n)
{
s=(a[i]&a[j]).count();
ans+=s*(s-1)/2;
}
}
break;
}
case 5:{
ans=n*(n-1)*(n-2)*(n-3)*(n-4)/10;
fo(i,1,n)
{
s=a[i].count();
ans-=s*(s-1)/2*(n-3)*(n-4);
}
fo(i,1,n-1)
{
fo(j,i+1,n)
{
A=a[i]&a[j];
s=A.count();
s1=c[i]-s-a[i][j];
s2=c[j]-s-a[j][i];
ans+=s*s1*s2+s*s1*(s-1)+s*(s-1)*s2+s*(s-1)*(s-2);
}
}
break;
}
}
printf("%lld\n",ans);
fclose(stdin);
fclose(stdout);
return 0;
}原文:https://www.cnblogs.com/gmh77/p/12459268.html