题目链接:https://www.luogu.com.cn/problem/P3233
世界树是一棵无比巨大的树,它伸出的枝干构成了整个世界。在这里,生存着各种各样的种族和生灵,他们共同信奉着绝对公正公平的女神艾莉森,在他们的信条里,公平是使世界树能够生生不息、持续运转的根本基石。
世界树的形态可以用一个数学模型来描述:世界树中有 \(n\) 个种族,种族的编号分别从 \(1\) 到 \(n\),分别生活在编号为 \(1\) 到 \(n\) 的聚居地上,种族的编号与其聚居地的编号相同。有的聚居地之间有双向的道路相连,道路的长度为 \(1\)。保证连接的方式会形成一棵树结构,即所有的聚居地之间可以互相到达,并且不会出现环。定义两个聚居地之间的距离为连接他们的道路的长度;例如,若聚居地 \(a\) 和 \(b\) 之间有道路,\(b\) 和 \(c\) 之间有道路,因为每条道路长度为 \(1\) 而且又不可能出现环,所以 \(a\) 与 \(c\) 之间的距离为 \(2\)。
出于对公平的考虑,第 \(i\) 年,世界树的国王需要授权 \(m_i\) 个种族的聚居地为临时议事处。对于某个种族 \(x\)(\(x\) 为种族的编号),如果距离该种族最近的临时议事处为 \(y\)(\(y\) 为议事处所在聚居地的编号),则种族 \(x\) 将接受 \(y\) 议事处的管辖(如果有多个临时议事处到该聚居地的距离一样,则 \(y\) 为其中编号最小的临时议事处)。
现在国王想知道,在 \(q\) 年的时间里,每一年完成授权后,当年每个临时议事处将会管理多少个种族(议事处所在的聚居地也将接受该议事处管理)。 现在这个任务交给了以智慧著称的灵长类的你:程序猿。请帮国王完成这个任务吧。
\(N\leq 300000\), \(q\leq 300000\), \(\sum^q_{i=1}m_i \leq 300000\)
调了 5 天,细节真的很多很烦。自闭到一度想要放弃233。
首先看见 \(m\) 的和不超过 \(3\times 10^5\),容易想到虚树。那么对于每一组询问,构建虚树后,分为 3 个部分来分别计算:
显然原树中的任意一个节点可以归属到上面三类中的一类的。
这个很好办。分别用两次 dfs 求出虚树上一个点 \(x\) 往下走和往上走能到达的最近关键节点即可。
具体来说,设 \(dep[x]\) 表示 \(x\) 在原树中的深度,\(dis[x]\) 表示 \(x\) 到关键节点的最短距离,\(pos[x]\) 表示 \(x\) 在哪个关键节点的管辖范围之内。
第一遍 dfs 遍历 \(x\) 的每一个子节点 \(y\),如果 \(dis[y]+dep[y]-dep[x]<dis[x]\) 或者两者相等且 \(pos[x]>pos[y]\),那么就用 \(pos[y]\) 来更新 \(pos[x]\)。
第二遍 dfs,对于 \(x\) 的父节点 \(fa\),判断 \(dis[fa]+dep[x]-dep[fa]\) 是否小于 \(dis[x]\)。其余和 1 一样。
什么意思?哪样例来说
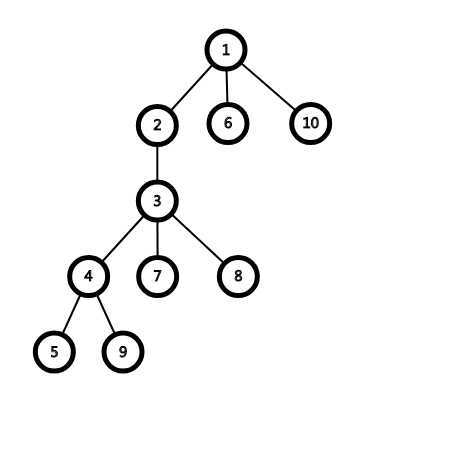
对于第二组询问2 7 3 6 9,以 3 号节点为例,他有三个子节点 4,7,8,其中 4,7 的子树中都有关键点,仅有 8 的子树中没有关键点,所以设 \(pos[4]=x\),那么原树中 8 节点的子树一定都归属于 \(x\)。
这一部分怎么计算呢?考虑用该节点原树中的大小减去虚树中的子树大小,因为不在虚树中的子节点一定没有关键节点后代。
那么这一部分也计算完了。
容易发现,对于虚树中的一条边 \(y\to x\),在原树中是一条链,且链上一定存在一个节点 \(p\),\(p\) 以下的节点全部归属于 \(pos[x]\),\(p\) 以上的节点全部归属于 \(pos[y]\)。
如何求出这个 \(p\)?既然满足单调,那么倍增即可。
注意不仅仅是这条链上的点,是这条链上的点以及他们的其他子树(不在虚树上的子树)节点一同归属。实在不是很好解释,画个图看看吧。
那么这三个部分都解决了。清空还是最傻的办法,直接开 \(\operatorname{set}\) 记录虚树中的点。显然有更好的方法但是懒。
细节真的很多,调样例可能都要调很久,然后交上去发现还 WA 了233。
\[\color{white}{\texttt{主要还是 stoorzTCL}}\]
时间复杂度 \(O(Q\log n)\)
很丑
#include <set>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=300010,LG=20,Inf=1e9;
int dep[N],head[N],dis[N],f[N][LG+1],dfn[N],a[N],id[N],st[N],pos[N],ans[N],size[N];
int n,Q,m,tot,top;
bool key[N];
set<int> vis;
struct edge
{
int next,to;
}e[N*2];
bool cmp(int x,int y)
{
return dfn[x]<dfn[y];
}
void add(int from,int to)
{
e[++tot].to=to;
e[tot].next=head[from];
head[from]=tot;
}
int lca(int x,int y)
{
if (dep[x]<dep[y]) swap(x,y);
for (int i=LG;i>=0;i--)
if (dep[f[x][i]]>=dep[y]) x=f[x][i];
if (x==y) return x;
for (int i=LG;i>=0;i--)
if (f[x][i]!=f[y][i])
x=f[x][i],y=f[y][i];
return f[x][0];
}
void dfs1(int x,int fa)
{
dfn[x]=++tot;
dep[x]=dep[fa]+1; f[x][0]=fa;
for (int i=1;i<=LG;i++)
f[x][i]=f[f[x][i-1]][i-1];
for (int i=head[x];~i;i=e[i].next)
if (e[i].to!=fa)
{
dfs1(e[i].to,x);
size[x]+=size[e[i].to];
}
size[x]++;
}
void build()
{
top=tot=0;
sort(a+1,a+1+m,cmp);
for (int i=1;i<=m;i++)
{
int p=lca(a[i],st[top]);
for (;top && dep[st[top-1]]>=dep[p];top--)
add(st[top-1],st[top]);
if (st[top]!=p) add(p,st[top]),st[top]=p;
st[++top]=a[i];
}
for (;top>=1;top--)
add(st[top-1],st[top]);
}
void dfs2(int x)
{
vis.insert(x); ans[x]=size[x];
for (int i=head[x];~i;i=e[i].next)
{
int v=e[i].to;
dfs2(v);
int dis2=dis[v]+dep[v]-dep[x];
if (dis2<dis[x] || (dis2==dis[x] && pos[v]<pos[x]))
dis[x]=dis2,pos[x]=pos[v];
}
if (key[x]) dis[x]=0,pos[x]=x;
}
void dfs3(int x,int fa)
{
int dis2=dis[fa]+dep[x]-dep[fa];
if (dis2<dis[x] || (dis2==dis[x] && pos[x]>pos[fa]))
dis[x]=dis2,pos[x]=pos[fa];
for (int i=head[x];~i;i=e[i].next)
dfs3(e[i].to,x);
}
int findson(int x,int y)
{
for (int i=LG;i>=0;i--)
if (dep[f[y][i]]>dep[x]) y=f[y][i];
return y;
}
void dfs4(int x)
{
for (int i=head[x];~i;i=e[i].next)
{
int v=e[i].to,p=findson(x,v);
ans[x]-=size[p];
dfs4(v);
}
if (pos[x]!=x && x) ans[pos[x]]+=ans[x];
}
void solve(int x,int y)
{
int p=x;
for (int i=LG;i>=0;i--)
{
int dis1=dis[x]+dep[x]-dep[f[p][i]];
int dis2=dis[y]+dep[f[p][i]]-dep[y];
if (dis1<dis2 || (dis1==dis2 && pos[x]<pos[y])) p=f[p][i];
}
ans[pos[x]]+=size[p]-size[x];
ans[pos[y]]+=size[findson(y,x)]-size[p];
}
void dfs5(int x)
{
for (int i=head[x];~i;i=e[i].next)
{
dfs5(e[i].to);
solve(e[i].to,x);
}
}
int main()
{
memset(head,-1,sizeof(head));
scanf("%d",&n);
for (int i=1,x,y;i<n;i++)
{
scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
tot=0; dfs1(1,0);
memset(head,-1,sizeof(head));
memset(dis,0x3f3f3f3f,sizeof(dis));
tot=0;
scanf("%d",&Q);
while (Q--)
{
scanf("%d",&m);
for (int i=1;i<=m;i++)
{
scanf("%d",&a[i]);
key[a[i]]=1; id[i]=a[i];
}
build();
dfs2(0); dfs3(0,0); //虚树上的点
dfs4(0); //没有关键点的子树
dfs5(0); //虚树中的边
for (int i=1;i<=m;i++)
printf("%d ",ans[id[i]]);
putchar(10);
for (set<int>::iterator it=vis.begin();it!=vis.end();it++)
head[*it]=-1,key[*it]=0,ans[*it]=0,dis[*it]=Inf;
vis.clear();
}
return 0;
}原文:https://www.cnblogs.com/stoorz/p/12466398.html