方程: a^2 + b^2 + c^2 = 1000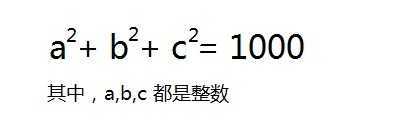
这个方程有整数解吗?有:a,b,c=6,8,30 就是一组解。
你能算出另一组合适的解吗?
请填写该解中最小的数字。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。

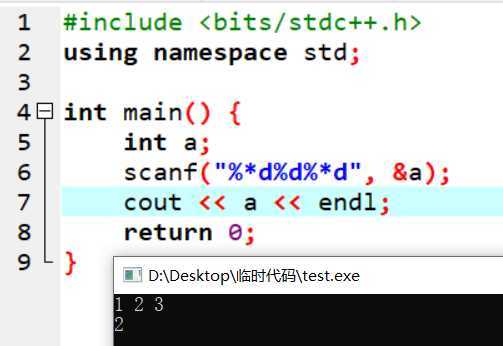
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int main() { 5 for(int i=1; i<=32; ++i) { 6 for(int j=i; j<=32; ++j) { 7 if((i*i+j*j) > 1000) continue; 8 for(int k=j; k<=32; ++k) { 9 if((i*i+j*j+k*k) == 1000) { 10 printf("%d %d %d\n", i, j, k); 11 } 12 } 13 } 14 } 15 return 0; 16 }
答案:10
在X星系的广袤空间中漂浮着许多X星人造“炸弹”,用来作为宇宙中的路标。
每个炸弹都可以设定多少天之后爆炸。
比如:阿尔法炸弹2015年1月1日放置,定时为15天,则它在2015年1月16日爆炸。
有一个贝塔炸弹,2014年11月9日放置,定时为1000天,请你计算它爆炸的准确日期。
请填写该日期,格式为 yyyy-mm-dd 即4位年份2位月份2位日期。比如:2015-02-19
请严格按照格式书写。不能出现其它文字或符号。

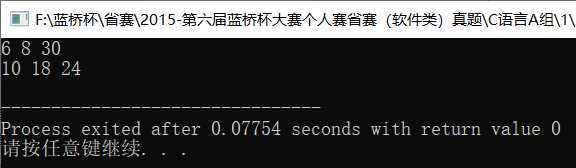
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int days[13] = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; 5 6 bool check(int y) { 7 if(y%400 == 0) return true; 8 if(y%4==0 && y%100!=0) return true; 9 return false; 10 } 11 12 int main() { 13 bool is_run = false; 14 int y = 2014, m = 11, d = 9, n = 1000; 15 for(int i=1; i<=n; ++i) { 16 d++; 17 if(m == 2) { 18 if(is_run) { 19 if(d >= 29) m++, d=0; 20 } 21 else { 22 if(d >= 28) m++, d=0; 23 } 24 } 25 else if(d>=days[m-1]) m++, d=0; 26 if(m > 12) { 27 y++, m=1; 28 is_run = check(y); 29 } 30 } 31 printf("%d-%02d-%02d\n", y, m, d); 32 return 0; 33 }
小明发现了一个奇妙的数字。它的平方和立方正好把0~9的10个数字每个用且只用了一次。
你能猜出这个数字是多少吗?
请填写该数字,不要填写任何多余的内容。

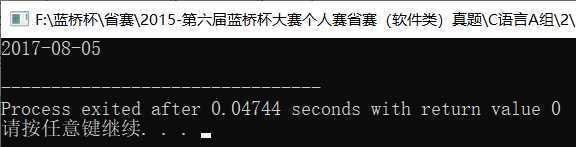
1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int cnt[11]; 5 6 void calc(int x) { 7 while(x) { 8 cnt[x%10]++; 9 x /= 10; 10 } 11 } 12 13 bool check(int x) { 14 int xx = x * x, xxx = x * x * x, len = 0; 15 for(int i=0; i<10; ++i) cnt[i] = 0; 16 bool flag = true; 17 calc(xx); calc(xxx); 18 for(int i=0; i<10; ++i) 19 if(cnt[i] == 0) flag = false; 20 return flag; 21 } 22 23 int main() { 24 int n = 9; 25 while(true) { 26 n++; 27 bool is_ok = check(n); 28 if(is_ok) break; 29 } 30 printf("%d\n", n); 31 return 0; 32 }
StringInGrid函数会在一个指定大小的格子中打印指定的字符串。
要求字符串在水平、垂直两个方向上都居中。
如果字符串太长,就截断。
如果不能恰好居中,可以稍稍偏左或者偏上一点。
下面的程序实现这个逻辑,请填写划线部分缺少的代码。
1 #include <stdio.h> 2 #include <string.h>
3 void StringInGrid(int width, int height, const char* s) { 4 int i,k; 5 char buf[1000]; 6 strcpy(buf, s); 7 if(strlen(s)>width-2) buf[width-2]=0; 8 9 printf("+"); 10 for(i=0;i<width-2;i++) printf("-"); 11 printf("+\n"); 12 13 for(k=1; k<(height-1)/2;k++){ 14 printf("|"); 15 for(i=0;i<width-2;i++) printf(" "); 16 printf("|\n"); 17 } 18 19 printf("|"); 20 21 printf("%*s%s%*s",____________); //填空 22 23 printf("|\n"); 24 25 for(k=(height-1)/2+1; k<height-1; k++){ 26 printf("|"); 27 for(i=0;i<width-2;i++) printf(" "); 28 printf("|\n"); 29 } 30 31 printf("+"); 32 for(i=0;i<width-2;i++) printf("-"); 33 printf("+\n"); 34 } 35 36 int main() { 37 StringInGrid(20,6,"abcd1234"); 38 return 0; 39 }
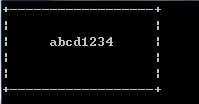
对于题目中数据,应该输出:
+------------------+
| |
| abcd1234 |
| |
| |
+------------------+
(如果出现对齐问题,参看【图1.jpg】)
注意:只填写缺少的内容,不要书写任何题面已有代码或说明性文字。
(width-2-strlen(buf))/2,"", buf, (width-1-strlen(buf))/2,""
1,2,3...9 这九个数字组成一个分数,其值恰好为1/3,如何组法?
下面的程序实现了该功能,请填写划线部分缺失的代码。
1 #include <stdio.h> 2 3 void test(int x[]) { 4 int a = x[0]*1000 + x[1]*100 + x[2]*10 + x[3]; 5 int b = x[4]*10000 + x[5]*1000 + x[6]*100 + x[7]*10 + x[8]; 6 7 if(a*3 == b) printf("%d / %d\n", a, b); 8 } 9 10 void f(int x[], int k) { 11 int i,t; 12 if(k>=9){ 13 test(x); 14 return; 15 } 16 17 for(i=k; i<9; i++) { 18 {t=x[k]; x[k]=x[i]; x[i]=t;} 19 f(x,k+1); 20 ___________________// 填空处 21 } 22 } 23 24 int main() { 25 int x[] = {1,2,3,4,5,6,7,8,9}; 26 f(x,0); 27 return 0; 28 }
注意:只填写缺少的内容,不要书写任何题面已有代码或说明性文字。
{t=x[k]; x[k]=x[i]; x[i]=t;}
小明被劫持到X赌城,被迫与其他3人玩牌。
一副扑克牌(去掉大小王牌,共52张),均匀发给4个人,每个人13张。
这时,小明脑子里突然冒出一个问题:
如果不考虑花色,只考虑点数,也不考虑自己得到的牌的先后顺序,自己手里能拿到的初始牌型组合一共有多少种呢?
请填写该整数,不要填写任何多余的内容或说明文字。
方法一:由于是直接提交答案,没有时间限制,我们可以暴力枚举每一张牌拿的张数,最后判断手里是不是13张。我的电脑运行时间在4.6s左右。

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int a[14], ans; 5 6 int main() { 7 for(a[1]=0; a[1]<=4; ++a[1]) 8 for(a[2]=0; a[2]<=4; ++a[2]) 9 for(a[3]=0; a[3]<=4; ++a[3]) 10 for(a[4]=0; a[4]<=4; ++a[4]) 11 for(a[5]=0; a[5]<=4; ++a[5]) 12 for(a[6]=0; a[6]<=4; ++a[6]) 13 for(a[7]=0; a[7]<=4; ++a[7]) 14 for(a[8]=0; a[8]<=4; ++a[8]) 15 for(a[9]=0; a[9]<=4; ++a[9]) 16 for(a[10]=0; a[10]<=4; ++a[10]) 17 for(a[11]=0; a[11]<=4; ++a[11]) 18 for(a[12]=0; a[12]<=4; ++a[12]) 19 for(a[13]=0; a[13]<=4; ++a[13]) { 20 int t = a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]+a[9]+a[10]+a[11]+a[12]+a[13]; 21 if(t == 13) ans ++; 22 } 23 printf("%d\n", ans); 24 return 0; 25 }
方法二:此时我们可以考虑dfs,发到第i种时,手里有j张,然后搜索+[0,4]的情况,即当前牌拿0-4张。第8行的剪枝很重要,不这样剪枝就要12s左右,这样剪枝需要0.2s左右

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int cnt; 5 6 void dfs(int i, int j) { // 发到第 i种牌 手里有 j张 7 if(i > 13) return; 8 if(j > 13) return; // 剪枝 当手里的牌数大于13张时,肯定不符合。 9 if(j == 13) { 10 cnt ++; 11 return ; 12 } 13 dfs(i+1, j); 14 dfs(i+1, j+1); 15 dfs(i+1, j+2); 16 dfs(i+1, j+3); 17 dfs(i+1, j+4); 18 } 19 20 int main() { 21 dfs(0, 0); 22 printf("%d\n", cnt); 23 return 0; 24 }
方法三:我们考虑DP。f[i][j]表示拿到第i种牌时,我们手里面有j张牌 的总数。那么我们的目标是不是就是f[13][13],即拿到第13种牌时,我们手里有13张牌。那么边界就是f[1][0-4] = 1;即我们只拿第1种时,拿0-4张都只有1种方法。转移方程为:f[i][j] = ∑jk=j-4f[i-1][k];代码如下:

1 #include <bits/stdc++.h> 2 using namespace std; 3 4 int f[14][14]; 5 6 int main() { 7 for(int i=0; i<=4; ++i) f[1][i] = 1; 8 for(int i=2; i<=13; ++i) { // 第 i种牌 9 for(int j=0; j<=13; ++j) { // 要拿 j 张 10 f[i][j] += f[i-1][j]; // 第 i种一张不拿 11 if(j-1>=0) f[i][j] += f[i-1][j-1];// 第 i种拿 1张 12 if(j-2>=0) f[i][j] += f[i-1][j-2];// 第 i种拿 2张 13 if(j-3>=0) f[i][j] += f[i-1][j-3];// 第 i种拿 3张 14 if(j-4>=0) f[i][j] += f[i-1][j-4];// 第 i种拿 4张 15 } 16 } 17 printf("%d\n", f[13][13]); 18 return 0; 19 }
2015-第六届蓝桥杯大赛个人赛省赛(软件类)真题 C大学A组
原文:https://www.cnblogs.com/Marginalin/p/12482655.html