//List和ArrayList的区别?用来存放所有Node的List public static List<Node> list=new ArrayList<Node>(); //由数组建树的方法 public void creatTree(int[] array){ //将数组改装成Node,放入list中,以方便后面创建完全二叉树 for(int i=0;i<array.length;i++){ Node btnode =new Node(array[i],null,null); list.add(btnode); } //首先在list的长度 大于1的情况下进行 //完全二叉树,假设所有Node个数为n,则前n/2个Node都是父节点,后一半都是叶子节点,没有子节点 //所以在创建二叉树中,只需要遍历0到n/2-1即,前一半数据,为他们在其子节点位置添加对应的lchild和rchild即可! //同时我们直到完全二叉树的假设该节点在数组的位置为i,且i<n/2,则其lchild节点为2i+1.rchild节点为2i+2. //当然,2i+1和2i+2都应该小于n才行! if(list.size()>0){ //for循环比较巧妙,注意for循环的次数,i代表的是每一个带有孩子的结点,0代表的是根节点 //长度为n的数组,0到n/2-1(包括n/2-1位置)为前一半数据 for(int i=0;i<array.length/2;i++){ if(2*i+1<list.size())//这里不能等于,原因是list的长度必须大于2*i+1不然会数组越界 list.get(i).setLchild(list.get(2 * i + 1)); if(2*i+2<list.size())// 这里也不能等于,原因是数组会越界 list.get(i).setRchild(list.get(2 * i + 2)); } } }
利用前面分析的特性2,可以通过针对对前一半的节点进行循环,依次判断其左子节点和右子节点是否依然存在,若存咋则连接上,否则null的方式来创建一个二叉树。
遍历二叉树;是一个基本的操作针对树这种结构来说,数组,链表,队列,stack等基本的线性结构的遍历很容易实现,但是在二叉树中,这是一个递归的结构,每一个节点又可以充当root进行遍历左右子节点,所以我们遍历二叉树中也采用递归遍历的方式。常规采用的方式有三种,前序遍历,中序遍历和后序遍历不同遍历的方区别在于,访问本节点的顺序,实在递归左子节点之前,之后,还是最后,下面用图来表示。
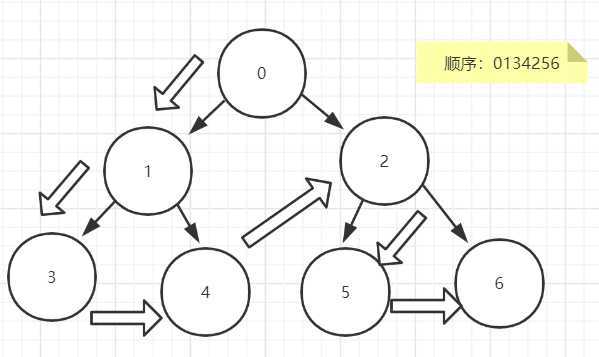
前序遍历;在向子节点遍历之前就已经遍历过本节点了,在本程序遍历本节点就相当于打印出来即可;在程序中,我们也可以看到,在向下递归之前就已经遍历本节点了。
//前序遍历 /** * 前序遍历的操作;先遍历根节点,在遍历左节点,再右节点, * 不断循环遍历即可,可采用递归的思想来遍历 * @param root 待遍历二叉树的根节点 */ public void preOrder(Node root){ //退出递归条件,若当前节点为null, //则return; if(root == null){ return ; } //否则则前遍历本节点,即直接打印 else{ System.out.println(root.val); } preOrder(root.lchild);//先遍历左子树 preOrder(root.rchild);//再遍历右子树 }
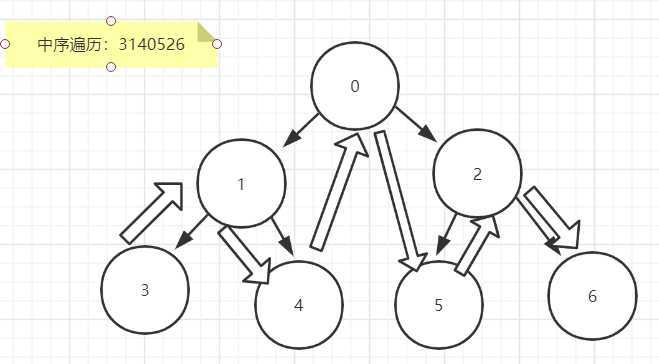
//中序遍历 public void inOrder(Node root){ //退出递归条件,若当前节点为null, //则return; if(root == null){ return ; } inOrder(root.lchild);//先遍历左子树 System.out.println(root.val);//再输出本节点 inOrder(root.rchild);//再遍历右子树 }
我们发小中序遍历和前序遍历在程序上,只是调节了
inOrder(root.lchild);//先遍历左子树
System.out.println(root.val);//再输出本节点
inOrder(root.rchild);//再遍历右子树
顺序,先遍历左子树,然后再本节点,或者先右子树,然后再本节点。
原文:https://www.cnblogs.com/dazhu123/p/12484647.html