一. 二叉树的定义:
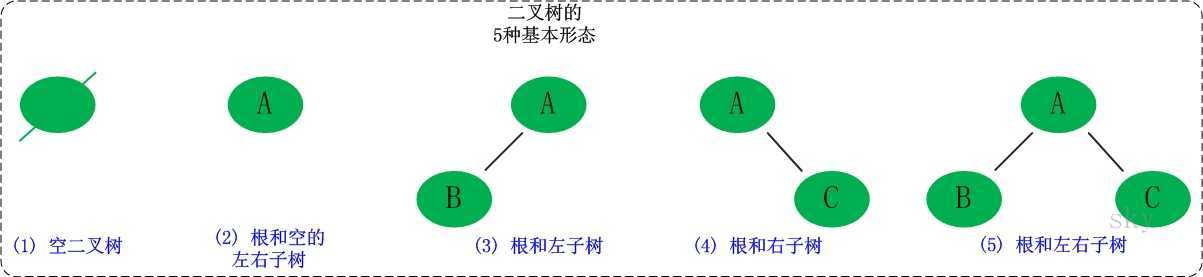
二叉树是每个节点最多有两个子树的树结构。它有五种基本形态:二叉树可以是空集;根可以有空的左子树或右子树;或者左、右子树皆为空。
直白的讲,二叉树只由三部分组成:根,左子树,右子树
但是,每个左子树与右子树同样也可以把自己看作根,因此,他们也有自己的左子树与右子树
结点的度:结点拥有的子树的数目
叶子结点:度为0的结点(tips:在任意一个二叉树中,度为0的叶子结点总是比度为2的结点多一个)
分支结点:度不为0的结点
树的度:树中结点的最大的度
层次:根结点的层次为1,其余结点的层次等于该结点的双亲结点的层次加1
树的高度:树中结点的最大层次
二。 二叉树的性质:
性质1:二叉树第i层上的结点数目最多为 2{i-1} (i≥1)。
性质2:深度为k的二叉树至多有2{k}-1个结点(k≥1)。
性质3:包含n个结点的二叉树的高度至少为log2 (n+1)。
性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1。
三。 二叉树的分类:
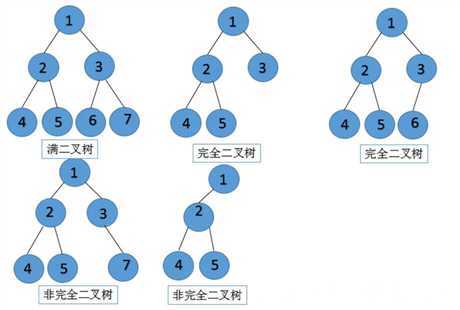
满二叉树:树内每一个节点都有左右两个子树。
完全二叉树:只有最后一层缺结点,且要么全缺,要么只缺右结点。
四。 二叉树的前中后序:
前中后序是三种遍历二叉树不同的方式
前序顺序:根 左 右
中序顺序:左 根 右
后序顺序:左 右 根
下面举个例子:
这个例子的三种顺序分别是:
前序:124563
中序:425613
后序:465231
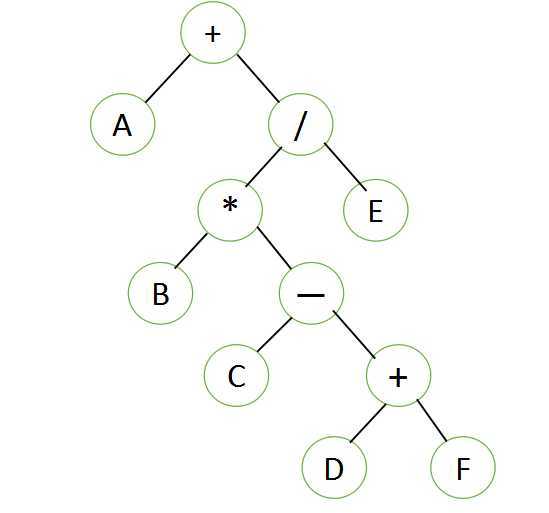
此表达式在我们人脑中应是(中序):A+B*[C-(D+F)]/E
前序:+A/*B-C+DFE
后序:ABCDF+-*E/+
五。 python遍历二叉树
# !/usr/bin/env python # coding=utf-8 """ python对二叉树的基本操作: 1,创建 2,遍历 """ class TreeNode: def __init__(self, value=None, left=None, right=None): self.value = value self.left = left # 左子树 self.right = right # 右子树 def preTraverse(root): ‘‘‘ 前序遍历 ‘‘‘ if root == None: return print(root.value) preTraverse(root.left) preTraverse(root.right) def midTraverse(root): ‘‘‘ 中序遍历 ‘‘‘ if root == None: return midTraverse(root.left) print(root.value) midTraverse(root.right) def afterTraverse(root): ‘‘‘ 后序遍历 ‘‘‘ if root == None: return afterTraverse(root.left) afterTraverse(root.right) print(root.value) if __name__ == ‘__main__‘: # root = TreeNode(‘D‘, TreeNode(‘B‘, TreeNode(‘A‘), TreeNode(‘C‘)), TreeNode(‘E‘, right=TreeNode(‘G‘, TreeNode(‘F‘)))) # root = TreeNode(‘D‘, TreeNode(‘B‘, TreeNode(‘A‘), TreeNode(‘C‘)), TreeNode(‘E‘, left=TreeNode(‘H‘,TreeNode(‘I‘),TreeNode(‘J‘)),right=TreeNode(‘G‘, TreeNode(‘F‘)))) root = TreeNode(‘+‘,TreeNode(‘A‘),TreeNode(‘/‘,TreeNode(‘*‘,TreeNode(‘B‘),TreeNode(‘-‘,TreeNode(‘C‘),TreeNode(‘+‘,TreeNode(‘D‘),TreeNode(‘F‘)))),TreeNode(‘E‘))) print(‘前序遍历:‘) preTraverse(root) print(‘\n‘) print(‘中序遍历:‘) midTraverse(root) print(‘\n‘) print(‘后序遍历:‘) afterTraverse(root) print(‘\n‘)
原文:https://www.cnblogs.com/yoyoma0355/p/12485768.html