0. 应用场景：修路问题

1. 最小生成树

1.1 定义

• 加权图：一种为每条边关联一个权值的图模型

• 图的生成树：是该连通图的一个极小连通子图，含有图的全部顶点，但只有构成一棵树的(n-1)条边
  

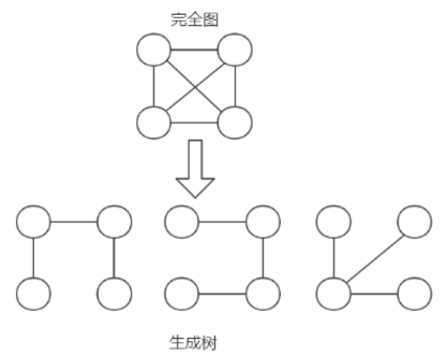
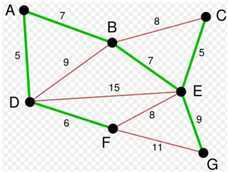
• 一幅加权图的最小生成树(MST)：在生成树的基础上，要求树的(n-1)条边的权值之和是最小的
  

1.2 一些约定

• 只考虑连通图
  • 根据树的基本性质，我们要找的就是一个由V-1条边组成的集合，他们既连通了图中的所有顶点而权值之和又最小
  • 如果一幅图是非连通的，我们只能使用这个算法来计算它的所有连通分量的最小生成树，合并在一起称其为"最小生成森林"
• 边的权重可能是0或者负数
• 所有边的权重都各不相同
  • 如果可以相同，MST就不一定唯一了

1.3 计算MST的两种算法

• Prim 算法
• Kruskal 算法

2. Prim 算法

• 从任意一个顶点开始，每次选择一个与 当前顶点集 最近的一个顶点，并将两顶点之间的边加入到顶点集中。然后继续找 离更新后的这个顶点集 最近的顶点 ....，就这么找下去，找够 n-1 条边
• {顶点集} 是逐渐增大的
• 找 {当前最近顶点} 时使用到了贪婪算法

2.1 思路

1. 设 G=(V,E) 是连通网，T=(U,D)是最小生成树，V,U是顶点集合，E,D是边的集合
2. 若从 顶点u 开始构造最小生成树，则从 集合V 中取出 顶点u 放入 集合U 中，标记 顶点v 的 visited[u]=1
3. 若 集合U 中 顶点ui 与 集合V-U 中的 顶点vj 之间存在边，则寻找这些边中权值最小的边，但不能构成回路，将 顶点vj 加入 集合U 中，将 边(ui,vj) 加入 集合D 中，标记 visited[vj]=1
4. 重复步骤②，直到 U 与 V 相等，即 所有顶点 都被标记为访问过，此时 D 中有 n-1 条边

2.2 代码实现

public class PrimDemo {
    public static void main(String[] args) {
        char[] datas = new char[] {'A','B','C','D','E','F','G'};
        int vertexs = datas.length;
        // 邻接矩阵 (∵ 是加权边 ∴ 表示两个顶点不连通得用个大数而非0)
        int[][] weightEdges = new int[][] {
            {10000,5,7,10000,10000,10000,2},
            {5,10000,10000,9,10000,10000,3},
            {7,10000,10000,10000,8,10000,10000},
            {10000,9,10000,10000,10000,4,10000},
            {10000,10000,8,10000,10000,5,4},
            {10000,10000,10000,4,5,10000,6},
            {2,3,10000,10000,4,6,10000}
        };
        
        MST mst = new MST();
        mst.createGraph(vertexs, datas, weightEdges);
        mst.showGraph();
        mst.prim(4);
    }
}

class MST {
    private Graph graph;
    
    public void createGraph(int vertexs, char[] datas, int[][] weightEdges) {
        graph = new Graph(vertexs);
        int i, j;
        for(i = 0; i < vertexs; i++) {
            graph.datas[i] = datas[i];
            for(j = 0; j < vertexs; j++)
                graph.weightEdges[i][j] = weightEdges[i][j];
        }
    }
    
    /**
     * 普利姆算法
     * @param v 从图的 v顶点 开始生成MST E.G. 'A' → 0, 'B' → 1 ...
     */
    public void prim(int v) {
        // 标记 顶点是否已被访问
        int[] visited = new int[graph.vertexs];
        // 把当前结点标记为 1
        visited[v] = 1;
        // 记录选定的2个顶点的索引
        int h1 = -1;
        int h2 = -1;
        
        int minWeight = 10000;
        // n个顶点, 找出 n-1 条边
        for(int k = 1; k < graph.vertexs; k++) {
            
            // 双重for: 确定 [新一次生成的子图(图越来越大)] 中, 哪两个顶点的权值最小
            // ~ 顶点i 表示被访问的结点(也同是子图中的顶点)
            for(int i = 0; i < graph.vertexs; i++) {
                // ~ 顶点j 表示还没有被访问的结点
                for(int j = 0; j < graph.vertexs; j++) {
                    // 子图越来越大, 需要if的次数也越来越多
                    if(visited[i] == 1 && visited[j] == 0 
                            && graph.weightEdges[i][j] < minWeight) {
                        minWeight = graph.weightEdges[i][j];
                        h1 = i;
                        h2 = j;
                    }
                }
            }
            System.out.printf("<%c, %c>\tweight = %d\n"
                    , graph.datas[h1], graph.datas[h2], minWeight);
            visited[h2] = 1;
            minWeight = 10000;
        }
    }
    
    public void showGraph() {
        graph.showGraph();
    }
}


class Graph {
    int vertexs; // 图中顶点个数
    char[] datas; // 顶点的值
    int[][] weightEdges; // 加权边
    
    public Graph(int vertexs) {
        this.vertexs = vertexs;
        datas = new char[vertexs];
        weightEdges = new int[vertexs][vertexs];
    }
    
    public void showGraph() {
        for(int[] link : weightEdges)
            System.out.println(Arrays.toString(link));
    }
}

42-MST & Prim算法

原文：https://www.cnblogs.com/liujiaqi1101/p/12489890.html