递归神经网络 RNN 原理(上)

前篇对于 RNN 前奏, 或者说是 NLP 的基础, 语言模型 (Language Model) 有了一点认识. LM 的应用场景为 在词库中, 搜索出 符合当前给定 句子的 下一个单词, 的所有可能单词的概率. 栗子还是还是 那个: students opened their __ 的空缺地方应该填啥 (从词库中搜索) . 主要呢是有聊到两种方式:

• n-gram
• fixed window

结论是, 都很菜. 真的很难去对词进行灵活选取的同时, 能有类似 "语义上下文分析" 的感觉在. 机器终究不是人呀. 人很轻易的做到, 但机器却始终是没有思维的. 但探索也不能停止不前哦.

RNN

于是呢, 在神经网络上, 深度递归就是可用来搞这些事情的.

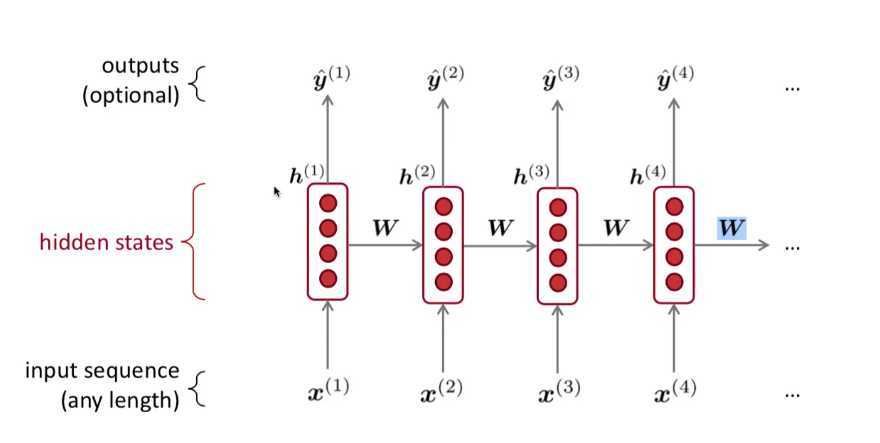
RNN 的核心思想是: Apply the same weights W repeatedly 重复地使用权值矩阵 W.

相当于是, \(Wx^{(1)}\) 作为一个全连接层的输出, 也可以是 当前的状态, 也可以一起结合 \(x^{(2)}\) 一起和上一个状态, 在产生一个新状态这样反复整.

RNN 作为一语言模型

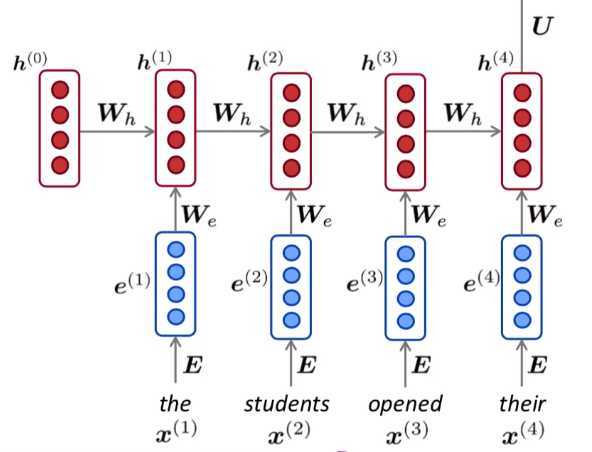
假如还是这4个单词, "the students opened their __ "

首先对每个词,其进行 onehot 编码, 会得到一个稀疏向量, 然后对其进行 encoding (图中的 E) 可以是 word2vec , 以达到将这个系数的长向量给, 变成 "稠密"的 新向量 e. (如图中)

然后用这稠密的向量 e 跟 W 相乘. 同时 给 h (隐含层) 进行一个初始化, 假设就全是0也可.计算方式是:

先走流程, 不用管 这些 W 是怎么来的.

\(We + Wh + bias\) 再在外面套一个激活函数(映射到 [0,1] 得到 \(h^{(1)}\) (新的向量)

然后, x2, x3, .. . 也都是同样的操作. 到了最后的 \(h^{(4)}\) 再将其与矩阵 U 相乘, 这个最终输出的向量作为 概率分布.

还是图结合公式更加直观一点呀:

(1) words / onehot vectors : \(x^{(t)} \in R^{|v|}\)

(2) word embeddings: \(e^{(t)} = Ex^{(t)}\)

(3) hidden states: \(\sigma(h^{(t)} = W_e e^{(t)} + W_h h^{(t-1)} + b_t)\) 注: \(h^{(0)}\) is the initial hidden state.

(4) output distribution: \(y^{(t)} = softmax(Uh^{(t)} + b_t) \in R^v\)

最后得到的 \(y^{(t)}\) 就是一个概率分布嘛. 值得注意的一点是, 这个 \(W_e\) 是复用的, 同样, 上面的 \(W_h\) 也是复用的, 这样做的特点是, RNN 对于输入向量的尺寸是没有限制的. 即可以用前面比如 5个单词来预测, 或者 10个单词来预测, 效果都是一样的.

RNN 优劣势

优:

• Can process any length
• 可以利用 many steps back 的信息
• 对输入的长度 不论是 3个还是4个还是多个单词, 起决定作用的是 W. 跟输入多, 少没啥关系的
• 对相同的单词, 因为 W 是复用的嘛, 因此相同单词, 尽管不同位置, 计算出来的值相同, 有种 "对称性"

劣:

• 递归地计算, 非常缓慢 (slow) 因为它要把上一个的输出,作为下一个的输入 (不断地 向量* 矩阵, 向量* 矩阵)..
• In practice, difficult to access information from many steps back. 实验上, 还是更多只利用了, 离它较为近的词的信息多一点, 虽然从公式上是看到所有的, 信息都输入了.

如何训练 RNN - LM

• Get a big corpus of text (大的语料库) which is a sequence of words \(x1, x^{(2)}...x^{(T)}\)

• Feed into RNN-LM; compute output distribution \(y^{(t)}\) for every step t (计算出每个状态的概率分布)
  • i.e. predict probability dist of every word, given words so far (给定前面单词, 去预测下一个单词, 然后再将前面的单词给加进去, 再继续预测下一个单词, 这样一直操作...)

• Loss function on step t is cross-entropy between predicted probability distribution \(y^{(t}\) and the true next word \(y^{(t)}\) (one hot for \(x^{(x+1)}\)) (在 t 时刻采用 交叉熵的方式) 相当于一个分类问题, 每个单词看作是一个独立的类别 , 将预测类别(最大概率) 和实际类别(语料库中) 的词是否能对得上. 跟前面的神经网络一样的做法, 将这个 误差 向后传递即可.

交叉熵

用来度量两个概率分布的差异信息.

在信息论中，交叉熵是表示两个概率分布p,q，其中p表示真实分布，q表示非真实分布，在相同的一组事件中，其中，用非真实分布q来表示某个事件发生所需要的平均比特数。

假设现在有一个样本集中两个概率分布p,q，其中p为真实分布，q为非真实分布。假如，按照真实分布p来衡量识别一个样本所需要的编码长度的期望为：

H(p)=

但是，如果采用错误的分布q来表示来自真实分布p的平均编码长度，则应该是：

H(p,q)=

此时就将H(p,q)称之为交叉熵。交叉熵的计算方式如下：

对于离散变量采用以下的方式计算：H(p,q)=

对于连续变量采用以下的方式计算：

交叉熵可在神经网络(机器学习)中作为损失函数，p表示真实标记的分布，q则为训练后的模型的预测标记分布，交叉熵损失函数可以衡量p与q的相似性。

交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题，因为学习速率可以被输出的误差所控制。

在特征工程中，可以用来衡量两个随机变量之间的相似度。

在语言模型中（NLP）中，由于真实的分布p是未知的，在语言模型中，模型是通过训练集得到的，交叉熵就是衡量这个模型在测试集上的正确率。

此处的损失函数就可以写成:

\(J^{(t)}(\theta) = CE (y^{(t)}, \hat y^{(t}) = -\sum \limits _{w \in V} y_w^{(t)} log \ \hat y_w^{(t)} = -log \ y^{(t)}_{x(t+1)}\)

这里V代表Vocabulary，语料库词汇

W代表权重参数，相当于 \(y^{(t)}\)是通过训练好的参数预测出来的。

这里交叉熵代表下一个词预测是分类任务，预测词汇表中哪一个词是下一个词

Average this to get overall loss for entire training set:

\(J^{(\theta)} = \frac {1}{T} \sum\limits _{t=1} ^T J^{(t)}(\theta) = \frac{1}{T} \sum\limits_{t=1}^T -log \ y^{(t)}_{x(t+1)}\)

还是蛮好理解的其实, 从整个过程来看.

RNN 过程

• Computing loss and gradients across entire corpus \(x^{(1)}, x^{(2)}, ...x^{(t)}\) is To expensive
  • \(J^{(\theta)} = \frac {1}{T} \sum\limits _{t=1} ^T J^{(t)}(\theta)\) 假设以 <<红楼梦>> 作为语料库, 那这个 T 就是要表示整本书的 字个数, 差不多有 820,000 字符, 然后还要 onehot, 再 encoding.. 这是相当大的.
• In practice, consider \(x^1, x^{(2)}...x^{(t)}\) as a sentence or a document. 降低计算量, 不通过逐字,一段一段整
• Recall: 可以用 SGD (随机梯度下降法) allow us to compute loss and gradients for small chunk of data, and update
• Compute loss \(J(\theta)\) for a sentence (actually a batch(小批量) of sentences), compute gradients and update weights. Repeat.

先到这吧, 下篇再接着来整, RNN 如何来做预测和 误差是如何 BP传播和RNN的应用场景等的认识.

递归神经网络 RNN 原理(上)

原文：https://www.cnblogs.com/chenjieyouge/p/12490996.html