先抛出一个问题,一棵n个点的树,每个点有一个不变的权值,m次询问任意两点之间的权值和。
最简单的算法:m次循环,每次从一个点出发,dfs累计走过的路径,直到到达另外一个点。
int dfs(int x,int fa,long long deep) { d[x]=deep; for(int i=head[x];i;i=nxt[i]) { int u=to[i];if(u==fa) continue; dfs(u,x,deep+w[i]); } }
如果你会前缀和,将其利用到树上,将一条条链想象成数组,于是乎我们就可以快速求出在一条链上的两点之间的权值和。
对于不在一条链上的点怎么办呢?我们求一下两点(a,b)的LCA,将(a,b)分为(lca,a)和(lca,b),这样lca和每一个点都在一条链上了。
void get_treesum(int x,int fa) { sum[x]=sum[fa]+a[x]; for(int i=head[x];i;i=nxt[i]) { int u=to[i];if(u==fa) continue; get_treesum(u,x); } } long long get_ans(int x,int y,int lca) { return sum[x]+sum[y]-sum[lca]-sum[fa[lca]]; }
如果还需要你支持一种操作:修改任意一个点的权值
我们还是先考虑处理的是数组,对于数组,我们不能再使用前缀和了,否则每次修改都是o(n)的,我们就可以使用线段树或者树状数组来维护这个数组,做到查询和修改都是o(logn)。
那对于树,可以把树看成很多数组组成的,那么我们可以直接套用线段树么?
显然不可以的,因为要用多棵线段树维护,那么单次修改的复杂度可能高达o(nlogn)。
那么可否用一棵线段树进行维护呢?我们姑且随便编一下号。id[x]表示x点在线段树上的位置。
对于修改o(logn),但是查询需要一个个点上去搜o(nlogn)。
显然线段树上单点操作和区间操作的复杂度是相同的,而我们每次操作或者查询的点的数量是一定的。
所以我们需要尽量多的区间操作,尽量少的单点操作使我们的总复杂度最小。
那么我们对于一条链的处理,最简单的就是从上到下id[x]依次增加,那么我们处理这条链的时候只需要一次区间操作。
但是问题是我们有很多链的处理,不可能满足每一条链自上而下的id都是依次增加的,只能挑选部分的链形成连续的id。
那我们肯定尽量挑选连续链 尽量长一些,这样造成区间处理的点可以更多,
比如说挑选的这条链从根节点出发延申,显然可以延申到深度最大的叶节点结果更优。
那么我们每次dfs到一个点,就将它节点数最大的儿子标记为重儿子。
void dfs1(int x,int fa) { son[x]=1;dep[x]=dep[fa]+1; for(int i=head[x];i;i=nxt[i]) { int u=to[i];if(u==fa) continue; dfs1(u,x);son[x]+=son[u]; if(son[u]>son[wson[x]]) wson[x]=son[u]; } }
在第二次dfs的时候,我们主要进行两个操作,一个是将x(dfs到的点)给一个线段树上的位置编号(该编号满足在dfs2完之后很多链的编号是连续的,实现线段树上尽可能多的区间处理),另一个操作是维护每个点的链首是谁。
链首是什么?就是你要处理形成的链的顶端(暂时不理解也没关系)。
void dfs2(int x,int topp) { topf[x]=topp;id[x]=++cnt; if(wson[x]) dfs2(wson[x],topp); for(int i=head[x];i;i=nxt[i]) { int u=to[i];if(u==wson[x]||u==fa[x]) continue; dfs2(u,u); } }
处理完之后可以得到类似下图,蓝字是id[],红点表示链首,粗线表示重链,细线表示轻链
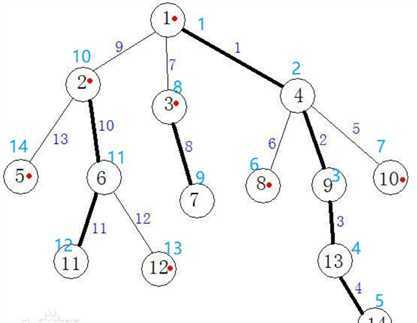
这样我们任意取一个点到根节点,可以发现处理次数均不大于3次。
下面给出从x到根节点最多经过2*logn条链的简单证明:
1.假设上方全部是轻链,那么假设当前走过一条轻链u→v(fa[u]==v),必定存在v的一个儿子的节点数大于son[u],那么走过这条轻链的时候,我们就已经至少有2*son[u]个点不需要操作了,每跳一次轻链就少处理当前儿子数的两倍,所以最多处理logn次。
2.假设上方全是重链,只需要一次线段树操作。
3.假设又有重链又有轻链,那么我们处理的不是重链就是轻链,处理完一次重链上面的链必定是轻链(如果重链上面是重链,那么他们显然可以连接在一起处理一次),所以走重链的次数和约等于走轻链的次数,那么最糟糕的情况就是走logn次轻链和logn次重链。
树链剖分非常依赖线段树的操作,线段树用的越好,链剖用的越好,下面是建线段树的操作。
#define lson o<<1 #define rson (o<<1)|1 void build_tree(int o,int l,int r) { if(l==r) {t[o]=a[l];return ;} int mid=(l+r)/2; build_tree(lson,l,mid);build_tree(rson,mid+1,r); }
t[o]中的o对应的是线段树的节点编号,而a[l]的l代表线段树的位置编号,所以我们需要在dfs2中加入下列操作:
topf[x]=topp;id[x]=++cnt;a[cnt]=v[x];
v[x]对应的是真实树上的x点的权值,x在线段树上的位置编号是cnt,所以a[]是过渡数组,将线段树节点编号和点权值相联系。
下面是修改真实树x节点的权值改为y(实际上就是线段树的单点修改):
void c_tree(int o,int l,int r,int pos,int val) { if(l==r) {t[o]=val;return ;} int mid=(l+r)/2; if(pos<=mid) c_tree(lson,l,mid,pos,val); else c_tree(rson,mid+1,r,pos,val); t[o]=t[lson]+t[rson]; } c_tree(1,1,n,id[x],y);
下面是我们查询一条链权值和的操作,因为是一条处理后的链,所以id是连续的(l,l+1,l+2......r-2,r-1,r),下面的查询操作:
LL quiry_tree(int o,int l,int r,int ll,int rr) { if(ll<=l&&rr>=r) return t[o]; int mid=(l+r)/2;LL ans=0; if(ll<=mid) ans+=quiry_tree(lson,l,mid,ll,rr); if(rr>mid) ans+=quiry_tree(rson,mid+1,r,ll,rr); return ans; }
那么我们现在处理两个点之间的权值和,我们已经可以处理一条链的权值和,我们现在只需要把两点之间的线段分成很多条链,我们两个点同时处理,每次先把 链首 深度 大的链先处理,然后该点跳到链首的父亲位置(点的位置都是没有处理的点),直到他们都跳到同一条链中(请想象),再处理这条链即可。
LL quiry_road(int x,int y) { LL ans=0; while(topf[x]!=topf[y]) //不是同一条链就跳 { if(dep[topf[x]]<dep[topf[y]]) swap(x,y); //每次处理链首深度大的 ans+=quiry_tree(1,1,n,id[topf[x]],id[x]); x=fa[topf[x]]; } if(dep[x]<dep[y]) swap(x,y); ans+=quiry_tree(1,1,n,id[y],id[x]); return ans; }
原文:https://www.cnblogs.com/tekim/p/shulianpoufen.html