Lecture10_几何1（介绍）_GAMES101 课堂笔记

课程回顾

这是课程7、8、9的上课内容：

本节课内容：

• 几何基础
  • 几何实例
  • 几何的表示法

几何应用举例

通过几个例子开启本节课的总结，下面主要列举4个例子：

• 图1是一些不同几何形状的杯子，会涉及如何设计出这些形状；
• 图2中的汽车引擎盖是非常光滑的曲面，会涉及如何用计算机模拟出如此光滑的面；
• 图3中形状各异的齿轮，对于这些复杂的几何构造如何表示；
• 图4中是一个蓝衣女子，会涉及如何表示薄纱不同厚度摊开与重叠时，不同的透明度表示问题；
  
  
  
  
  
  
  
  
  
  

下面将介绍几何表示方法：
主要分为implicit（隐式） 和Explicit(显式)两大类方法，以下是方法概览：

一、Implicit（隐式）表示法

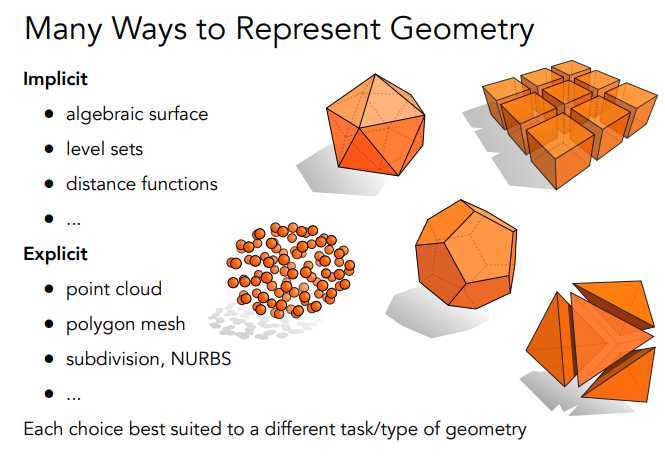
通过告诉点关系，对点进行归类，从而判断几何关系（是否在几何表面等关系）。

• 优点：很容易判断几何关系（带入隐式即可算出。）
• 缺点：但是很难从隐式关系式看出几何形状。
  

下面将介绍 5 种隐式表示方法：
隐式表示方法概览：

（ 一 ）代数曲面法（Algebraic Surfaces）

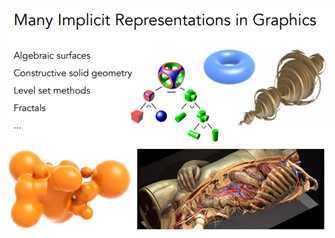
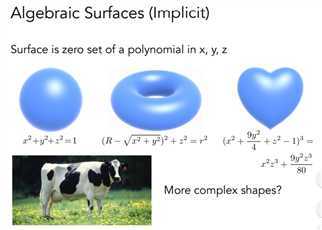
这种方法，主要是很难从数学式子看出形状，并且很难表示复杂的形状。

（ 二 ）构造实体几何法（Constructive Solid Geometry ）

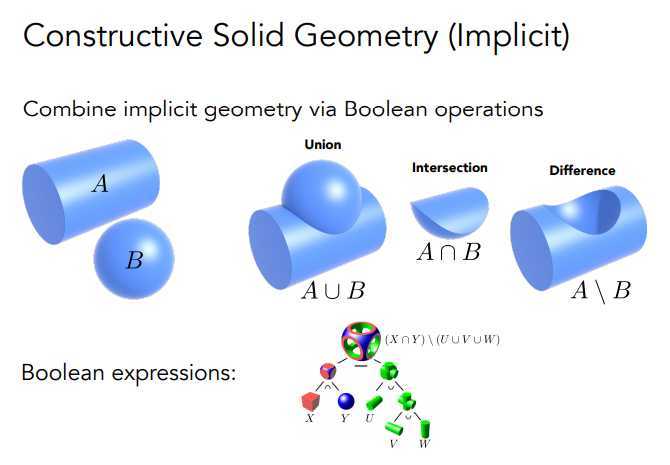
这种方法通过使用简单额几何体进行Bool运算，就可构造出复杂的形状。

（ 三 ）距离函数法（Distance Functions）

通过定义一个距离函数，表示两个物体的距离关系。（不直接描述表面，而是描述一个点到表面的最近距离。），由此通过最小距离判断出在几何体的表面上、外、内关系（加入对应数值0、+、-）。

举例：
想通过A、B得到移动融合运动边界（假设划线为黑色，空白为白色），但是直接做出的结果\(blend(A,B)\)得出的颜色将会是黑、灰、白（AB重合区域、B-A区域、空白区域）。这并不是我们想要得到的黑白融合结果。

于是，使用有向距离函数（Signed-distance Function，简称SDF），通过\(-,0,+\)表示关系，再将\(SDF(A)\)与\(SDF(B)\)做融合，最后将其还原，即可得到\(blend(SDF(A),SDF(B))\)中0为分割线，左边伟黑色，右边为白色的理想结果。

融合距离函数有很多应用，比如下图，这种方法的表示能力极强，可清楚看见瓢虫、蘑菇草相互融合的画面。

（ 四 ）水平集法（Level Set Methods）

这种方法与距离函数方法类似，找临界面等于0处（类似等高线），在二维、三维空间中均可使用，找出\(f(x)\)值相等的所有点即可找出一个平面。

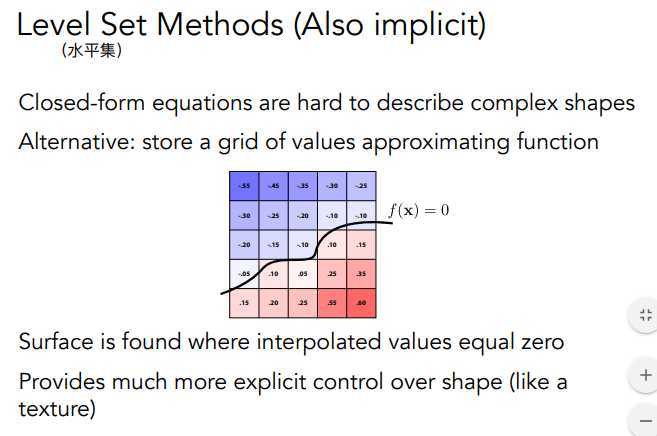
应用举例:模拟水圈形成

（ 五 ）分型法（Fractals）

“分型”是指一个大物体由一些形状相同的小物体组成，小物体又由一些形状相同的更小物体组成，即“自相似”（类似递归思想）。

二、Explicit(显式)表示法

显式表示法主要有两种：

1. 将表面上的点表示出来（例如之前的用像素点表示三角形的面）
2. 用参数映射方法（上图中，本文主要介绍这种方法）。

其中参数映射方法从式子\(f : \Bbb{R^2} \rightarrow \Bbb{R^3} ; \left(u,v\right) \mapsto \left(x,y,z\right)\),即可将一个二维平面\(\left(u,v\right)\)映射到三维平面\(\left(x,y,z\right)\)中。

• 优点：很容易看出几何形状，通过映射关系即可知道。
• 缺点：但是很难从显式关系式判断几何关系

三、小结

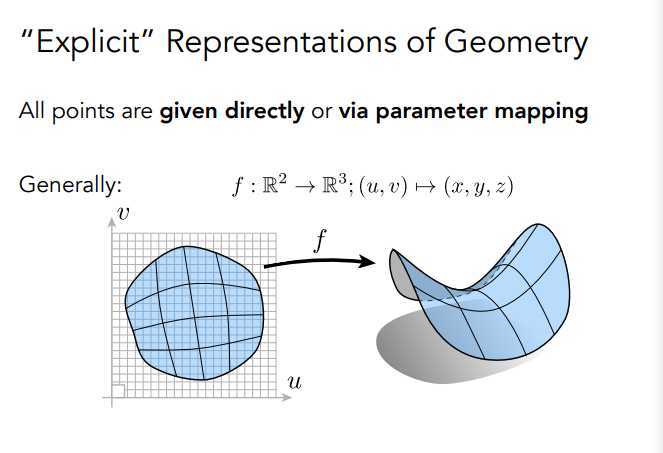
关于显式和隐式表示法，他们各有不同的优缺点，可根据实际应用场景选择不同的表示方法。

Lecture10_几何1（介绍）_GAMES101 课堂笔记

原文：https://www.cnblogs.com/somedayLi/p/12495272.html