在平面解析几何中,圆的方程可以描述为\((x – x_0)^2 + (y – y_0)^2 = R^2\),其中\((x_0, y_0)\)是圆心坐标,\(R\)是圆的半径,特别的,当\((x_0, y_0)\)就是坐标中心点时,圆方程可以简化为\(x^2 + y^2 = R^2\)。在计算机图形学中,圆和直线一样,也存在在点阵输出设备上显示或输出的问题,因此也需要一套光栅扫描转换算法。为了简化,我们先考虑圆心在原点的圆的生成,对于中心不是原点的圆,可以通过坐标的平移变换获得相应位置的圆。
在进行扫描转换之前,需要了解一个圆的特性,就是圆的八分对成性。如图(1)所示:
图(1)圆的八分对成性
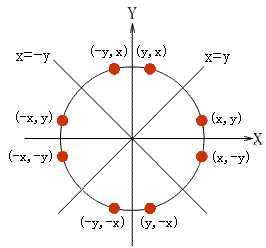
圆心位于原点的圆有四条对称轴\(x = 0\)、\(y = 0\)、\(x = y\)和\(x = -y\),若已知圆弧上一点\(P(x,y)\),就可以得到其关于四条对称轴的七个对称点:\((x, -y)\)、\((-x, y)\)、\((-x, -y)\)、\((y, x)\)、\((y, -x)\)、\((-y, x)\)、\((-y, -x)\),这种性质称为八分对称性。因此只要能画出八分之一的圆弧,就可以利用对称性的原理得到整个圆。
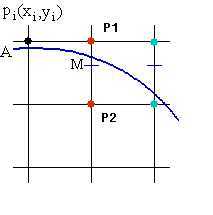
考虑圆心在原点,半径为\(R\)的圆在第一象限内的八分之一圆弧,从点\((0, R)\)到点\((R' , R')\)顺时针方向确定这段圆弧。假定某点\(P_i(x_i, y_i)\)已经是该圆弧上最接近实际圆弧的点,那么\(P_i\)的下一个点只可能是正右方的\(P_1\)或右下方的\(P_2\)两者之一,如图(2)所示:
图(2)中点划线法示例
构造判别函数:
\[
F(x,y)=x^2+y^2-R^2
\]
当\(F(x, y)= 0\),表示点在圆上,当\(F(x, y)> 0\),表示点在圆外,当\(F(x, y)< 0\),表示点在圆内。如果\(M\)是\(P_1\)和\(P_2\)的中点,则\(M\)的坐标是\((x_i + 1, y_i – 0.5)\),当\(F(x_i + 1, y_i – 0.5)< 0\)时,\(M\)点在圆内,说明\(P_1\)点离实际圆弧更近,应该取\(P_1\)作为圆的下一个点。同理分析,当\(F(x_i + 1, y_i – 0.5)> 0\)时,\(P_2\)离实际圆弧更近,应取\(P2\)作为下一个点。当\(F(x_i + 1, y_i – 0.5)= 0\)时,\(P_1\)和\(P_2\)都可以作为圆的下一个点,算法约定取\(P_2\)作为下一个点。
现在将\(M\)点坐标\((x_i + 1, y_i – 0.5)\)带入判别函数\(F(x, y)\),得到判别式\(d\):
\[
d = F(x_i + 1, y_i – 0.5)= (x_i + 1)^2 + (y_i – 0.5)^2 – R^2
\]
若\(d < 0\),则取\(P_1\)为下一个点,此时\(P_1\)的下一个点的判别式为:
\[
d’ = F(x_i + 2, y_i – 0.5)= (x_i + 2)^2 + (y_i – 0.5)^2 – R^2
\]
展开后将\(d\)带入可得到判别式的递推关系:
\[
d’ = d + 2x_i + 3
\]
若\(d > 0\),则取\(P_2\)为下一个点,此时\(P_2\)的下一个点的判别式为:
\[
d’ = F(x_i + 2, y_i – 1.5)= (x_i + 2)^2 + (y_i – 1.5)^2 – R^2
\]
展开后将d带入可得到判别式的递推关系:
\[
d’ = d + 2(x_i - y_i) + 5
\]
特别的,在第一个象限的第一个点\((0, R)\)时,可以推倒出判别式\(d\)的初始值\(d_0\):
\[
d_0 = F(1, R – 0.5) = 1 – (R – 0.5)^2 – R^2 = 1.25 - R
\]
根据上面的分析,可以写出中点画圆法的算法。考虑到圆心不在原点的情况,需要对计算出来的坐标进行了平移,下面就是通用的中点画圆法的源代码:
// 参数xc和yc是圆心坐标,r是半径,CirclePlot()函数是参照圆的八分对称性完成八个点的位置计算的辅助函数。
void MP_Circle(int xc , int yc , int r) {
int x, y;
double d;
x = 0;
y = r;
d = 1.25 - r;
CirclePlot(xc , yc , x , y);
while(x < y) {
if(d < 0) {
d = d + 2 * x + 3;
} else {
d = d + 2 * ( x - y ) + 5;
y--;
}
x++;
CirclePlot(xc , yc , x , y);
}
}
#include<stdio.h>
#include<graphics.h>
#include<conio.h>
#define x0 400
#define y0 300 //定义全局变量x0,y0:坐标轴中心(x0,y0)
void Middle_point_draw_circle(int x1, int y1, int r) {
int d0, x = 0, y = r;//d0是判别式的值
d0 = 1.25 - r; //判别式的初始值,1.25可以改为1
while (x < y) {
if (d0 >= 0) {
d0 = d0 + 2 * (x - y) + 5; //d0一定要先比x,y更新
x += 1; //因为d0表达式中的x,y是上一个点
y -= 1;
putpixel(((x + x1) + x0), (y0 - (y + y1)), RED); //(x,y)
putpixel(((-x + x1) + x0), (y0 - (y + y1)), RED); //(-x,y)
putpixel(((y + x1) + x0), (y0 - (x + y1)), RED); //(y,x)
putpixel(((-y + x1) + x0), (y0 - (x + y1)), RED); //(-y,x)
putpixel(((x + x1) + x0), (y0 - (-y + y1)), RED); //(x,-y)
putpixel(((-x + x1) + x0), (y0 - (-y + y1)), RED); //(-x,-y)
putpixel(((y + x1) + x0), (y0 - (-x + y1)), RED); //(y,-y)
putpixel(((-y + x1) + x0), (y0 - (-x + y1)), RED); //(-y,-x)
Sleep(50);
} else {
d0 = d0 + 2 * x + 3;
x += 1;
y = y;
putpixel(((x + x1) + x0), (y0 - (y + y1)), RED); //(x,y)
putpixel(((-x + x1) + x0), (y0 - (y + y1)), RED); //(-x,y)
putpixel(((y + x1) + x0), (y0 - (x + y1)), RED); //(y,x)
putpixel(((-y + x1) + x0), (y0 - (x + y1)), RED); //(-y,x)
putpixel(((x + x1) + x0), (y0 - (-y + y1)), RED); //(x,-y)
putpixel(((-x + x1) + x0), (y0 - (-y + y1)), RED); //(-x,-y)
putpixel(((y + x1) + x0), (y0 - (-x + y1)), RED); //(y,-y)
putpixel(((-y + x1) + x0), (y0 - (-x + y1)), RED); //(-y,-x)
Sleep(50);
}
}
}
int main() {
int x1, y1, r;
printf("请输入中点画圆算法圆心坐标(x1,y1)和圆的半径r:\n");
scanf("%d %d %d", &x1, &y1, &r);
initgraph(x0 * 2, y0 * 2); //初始化图形窗口大小
setbkcolor(WHITE);
cleardevice();
setcolor(BLACK);
line(x0, 0, x0, y0 * 2); //坐标轴X
line(0, y0, x0 * 2, y0); //坐标轴Y
Middle_point_draw_circle(x1, y1, r); //中点画圆算法
getch(); //等待一个任意输入结束
closegraph(); //关闭图形窗口
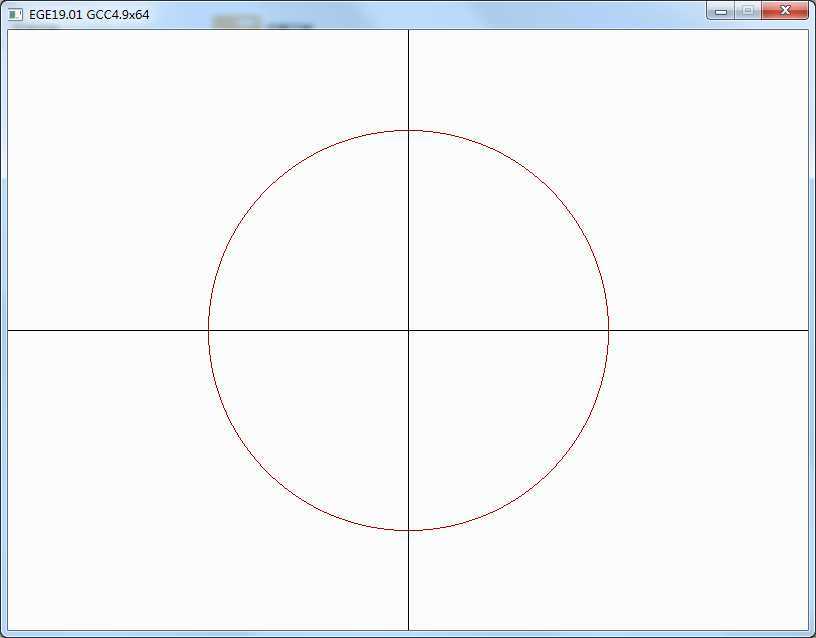
}中点画圆法中,计算判别式\(d\)使用了浮点运算,影响了圆的生成效率。如果能将判别式规约到整数运算,则可以简化计算,提高效率。于是人们针对中点画圆法进行了多种改进,其中一种方式是将\(d\)的初始值由\(1.25 – R\)改成\(1 – R\),考虑到圆的半径\(R\)总是大于\(2\),因此这个修改不会影响d的初始值的符号,同时可以避免浮点运算。还有一种方法是将\(d\)的计算放大两倍,同时将初始值改成\(3 – 2R\),这样避免了浮点运算,乘二运算也可以用移位快速代替,采用\(3 – 2R\)为初始值的改进算法,又称为Bresenham算法
void Bresenham_Circle(int xc , int yc , int r) {
int x, y, d;
x = 0;
y = r;
d = 3 - 2 * r;
CirclcPlot(xc , yc , x , y);
while(x < y) {
if(d < 0) {
d = d + 4 * x + 6;
} else {
d = d + 4 * ( x - y ) + 10;
y--;
}
x++;
CirclePlot(xc , yc , x , y);
}
}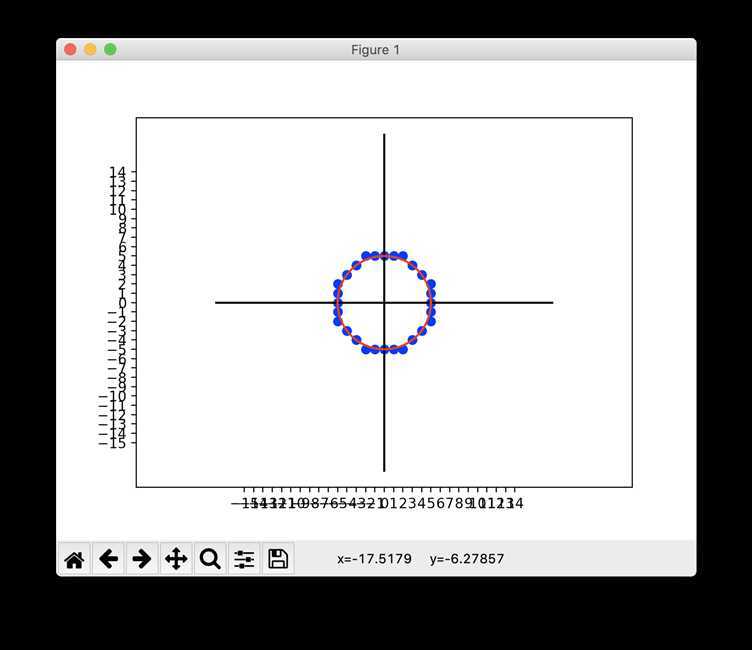
# Bresenham画圆
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation
import random as rd
# ==========================================
# 圆的基本信息
# 1.圆半径
r = 6.0
# 2.圆心坐标
a, b = (0., 0.)
Ary = []
Aryd = []
# ==========================================
# Bresenham计算点的方法
# 画点方向 只有右下L点或者正右H点
# 计算D(H) D(L) 计算公式为D(p)=px*px+py*py-r*r
# 计算di=D(H)+D(L) di>0则画L,di<=0则画H
# 考虑圆的对称性根据L点坐标依次画出(x,y),(-x,y),(-x,-y),(x,-y),(y,x),(-y,x),(-y,-x),(y,-x)八个点
# 起止位置(0,r)到(r-1,y),因为终点没有好的方法可以判断到底划分到那里
# 为了适合大多数半径还是使用上面的终点,虽然会多画几个点,不过消耗很少
# def init():
# plt.set_xlim(Ary[
def getPoint():
R = int(r)
st = [0, R]
Ary.append(st)
plt.scatter(0, R, color='b')
plt.scatter(0, -R, color='b')
plt.scatter(-R, 0, color='b')
plt.scatter(R, 0, color='b')
for i in range(0, R-1):
H = [st[0]+1, st[1]]
L = [st[0]+1, st[1]-1]
DH = H[0]*H[0]+H[1]*H[1]-R*R
DL = L[0]*L[0]+L[1]*L[1]-R*R
di = DH+DL
Aryd.append(di)
if(di > 0):
H = L
st = H
Ary.append(st)
DrawPoint(st[0], st[1], 'b')
def DrawPoint(x, y, cr):
plt.scatter(x, y, color=cr)
plt.scatter(-x, y, color=cr)
plt.scatter(-x, -y, color=cr)
plt.scatter(x, -y, color=cr)
plt.scatter(y, x, color=cr)
plt.scatter(-y, x, color=cr)
plt.scatter(-y, -x, color=cr)
plt.scatter(y, -x, color=cr)
def setAxis():
lent = range(-15, 15, 1)
plt.xticks(lent)
plt.yticks(lent)
plt.plot([-18, 18], [0, 0], 'k')
plt.plot([0, 0], [-18, 18], 'k')
# 参数方程画圆
def drawCle():
theta = np.arange(0, 2*np.pi, 0.01)
x = a + r * np.cos(theta)
y = b + r * np.sin(theta)
plt.plot(x, y, 'r')
plt.axis('equal')
# plt.show()
if __name__ == "__main__":
# r=float(input("r:"))
r = int(rd.uniform(3, 15)+0.5)
# r=8
setAxis()
getPoint()
drawCle()
print(Ary)
print(Aryd)
plt.show()
原文:https://www.cnblogs.com/iamfatotaku/p/12497354.html