(引用自:https://blog.csdn.net/qq_28031525/article/details/79596376)
度量文本相似度包括如下三种方法:
一是基于关键词匹配的传统方法,如N-gram相似度;
二是将文本映射到向量空间,再利用余弦相似度等方法;
相似度就是比较两个事物的相似性。一般通过计算事物的特征之间的距离,如果距离小,那么相似度大;如果距离大,那么相似度小。
问题定义:有两个对象X、Y,都包括N维特征,X=(x1,x2,x3,..,xn),Y=(y1,y2,y3,..,yn)X=(x1,x2,x3,..,xn),Y=(y1,y2,y3,..,yn),计算X和Y的相似性。常用的方法如下:
2.4.1 欧式距离
欧氏距离是最常用的距离计算公式,衡量的是多维空间中各个点之间的绝对距离,当数据很稠密并且连续时,这是一种很好的计算方式。
因为计算是基于各维度特征的绝对数值,所以欧氏度量需要保证各维度指标在相同的刻度级别,如在KNN中需要对特征进行归一化。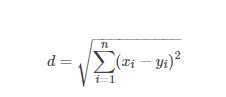
2.4.2 曼哈顿距离
曼哈顿距离也称为城市街区距离(City Block distance)。

2.4.3 余弦相似度
余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量,余弦相似度更加注重两个向量在方向上的差异,而非距离或长度上。
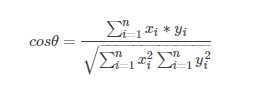
2.4.4 其他
其他的相似度计算方法包括皮尔森相关系数、一般化的闵可夫斯基距离(当p=1时为曼哈顿距离,当p=2时为欧式距离)、汉明距离等。
三是深度学习的方法
如基于用户点击数据的深度学习语义匹配模型DSSM,
基于卷积神经网络的ConvNet,
以及目前state-of-art的Siamese LSTM等方法。
ESIM
(当然这里面构造到的相邻矩阵也可以抽出来单独做一种)
模型介绍:
https://www.cnblogs.com/qniguoym/p/7772561.html
模型介绍2:
原文:https://www.cnblogs.com/tfknight/p/12501125.html