我们为什么要引进p-adic?
一方面,在function theory中我们有power series expansion,而我们知道,Z上的数可以视作是C[z]里,定义域是Z上的素数空间的多项式。一个自然的问题是,我们能够利用Taylor expansion定义多项式的高阶导数,我们也想定义某种Z中数的类似结果。
另一方面,我们考虑丢番图方程。






我们可以自然地把Z和Q嵌入p-adic integer和p-aidc number里面。通过这一操作,我们可以把整数或是有理数进行类似Talor expansion的操作了:



考虑丢番图方程,



必要性是显然的,给出充分性的证明:


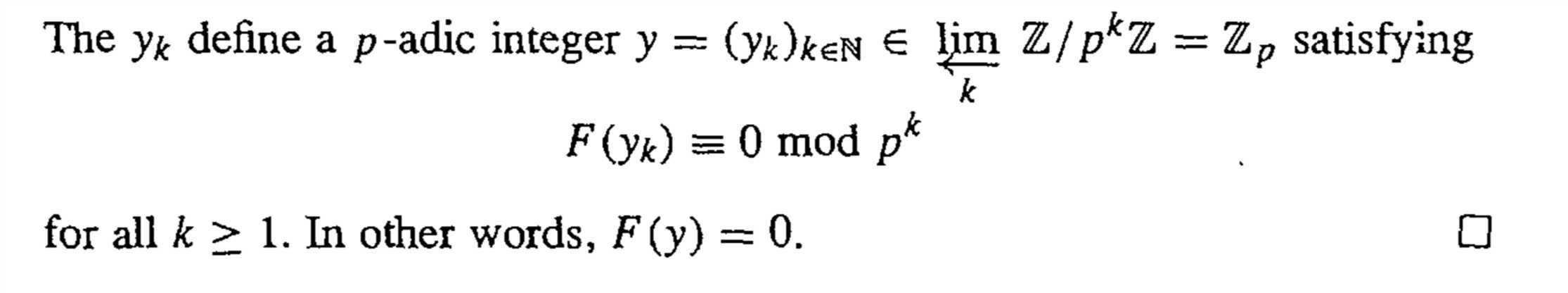
Remark:上面的定理告诉我们在p-adic域上解丢番图方程等价于在所有的p的n阶域上解方程,而考虑椭圆曲线上的有理点时,我们也有定理说明只需要所有p-adic number field上考虑,这就是第二个要考虑p-adic number的原因。
我们考虑p-adic value的原因是我们想要p-adic number converges。

我们回忆在function field里面我们也定义了valuation:




另一种定义p-adic number的方式是通过完备化,再次不提。


这些都在离散赋值环中做过讨论。
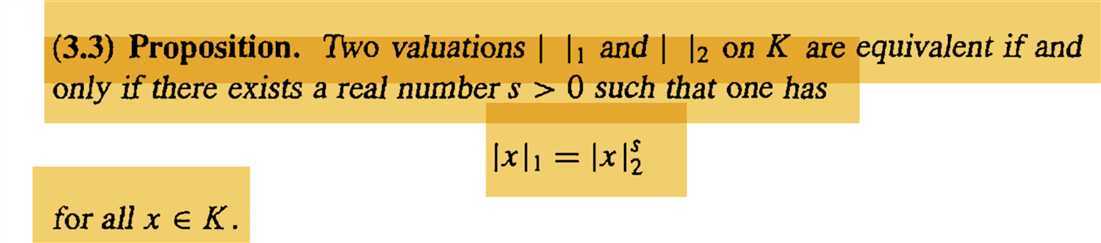










The p-adic Numbers & The p-adic Absolute Value & Valuations
原文:https://www.cnblogs.com/zny14/p/12500980.html