归并排序利用了分治策略。在分治策略中,我们递归地求解一个问题,在每层递归中应用如下三个步骤:
当子问题足够大,需要递归求解时,我们称之为递归情况。当子问题变得足够小时,不再需要递归,我们说递归已经触底,进入了基本情况。有时,除了与原问题形式完全一样的规模更小的子问题外,还需要求解与原问题不一样的子问题。我们将这些子问题的求解看作合并步骤的一部分。
最大子数组问题
假定我们要寻找数组 A[ p , r ] 的最大子数组。 A[ p , r ] 的任何连续子数组 A[ i , j ] 所处的位置必然是以下三种情况:
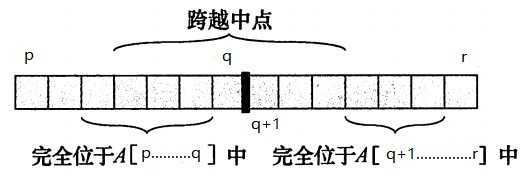
我们可以递归地求解 A[ p , q ] 和 A[ q+1 , r ] 的最大子数组,因为这两个子问题仍是最大子数组问题,用另一种方法寻找跨越中点的最大子数组,然后在三种情况中选取和最大者。
代码示例
template<class T> struct subArray{//子数组结构体 int left, right; T sum; };
//寻找跨越中点的最大子数组 template<class T> subArray<T> FindMaxCrossingSubArray(T a[], int p, int q, int r) { T leftSum = min, rightSum = min; T sum = 0; int leftI = -1, rightI = -1; for (int i = q; i >= p; i--) { sum += a[i]; if (sum > leftSum) { leftSum = sum; leftI = i; } }
sum = 0; for (int i = q + 1; i <= r; i++) { sum += a[i]; if (sum > rightSum) { rightSum = sum; rightI = i; } }
subArray<T> result; result.left = leftI; result.right = rightI; result.sum = leftSum + rightSum; return result; }
//寻找最大子数组 template<class T> subArray<T> FindMaxSubArray(T a[], int p, int r) { subArray<T> result; if (p == r) {//只有一个元素 result.left = p; result.right = r; result.sum = a[p]; return result; }
int q = (p + r) / 2; subArray<T> leftArray, rightArray, crossArray; leftArray = FindMaxSubArray(a, p, q);//寻找最大左子数组 rightArray = FindMaxSubArray(a, q + 1, r);//寻找最大右子数组 crossArray = FindMaxCrossingSubArray(a, p, q, r);//寻找跨越中点的最大子数组
//三种情况中选取最大值 if (leftArray.sum > rightArray.sum&&leftArray.sum > crossArray.sum) { result.left = leftArray.left; result.right = leftArray.right; result.sum = leftArray.sum; } else if (rightArray.sum > leftArray.sum&&rightArray.sum > crossArray.sum) { result.left = rightArray.left; result.right = rightArray.right; result.sum = rightArray.sum; } else if (crossArray.sum > leftArray.sum&&crossArray.sum > rightArray.sum) { result.left = crossArray.left; result.right = crossArray.right; result.sum = crossArray.sum; } return result; }
57
原文:https://www.cnblogs.com/bjxqmy/p/12503224.html