由$f(x)=k$型方程根的个数求参数的范围

前言

类型列举

曲线静，直线动，一静一动型

例1已知函数\(f(x)=x^2+\cfrac{m}{x}-3\)有三个不同的零点，求参数\(m\)的范围。

分析：由题目先转化为方程\(x^2+\cfrac{m}{x}-3=0\)有三个不同的实根，

分离参数得到，方程\(-m=x^3-3x(x\neq 0)\)有三个不同的实根，

令\(g(x)=x^3-3x(x\neq 0)\)，用导数方法求其单调区间，为作图做准备。

令\(g'(x)=3x^2-3>0\)，得到\(x<-1\)或\(x>1\)；

令\(g'(x)<0\)，得到\(-1<x<1\)，\(x\neq 0\)最后做处理。

则函数\(g(x)\)在\((-\infty，-1]\) 上单调递增，

在\([-1，1]\)上单调递减，在\([1，+\infty)\)上单调递增；

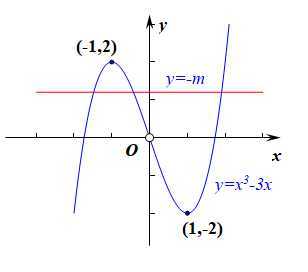
又\(g(-1)=2\)，\(g(1)=-2\)，手工作图如右，

在同一个坐标系中做\(y=-m\)和\(y=g(x)\)的图像，

由图像可得，\(-2<-m<2\)，且\(-m\neq 0\)，

解得\(m\)的取值范围为\((-2,0)\cup(0，2)\)。

感悟反思：
1、分离参数法，
2、数形结合思想。
3、形如函数\(f(x)=g(x)-a\)有\(n\)个零点的问题，常常就转化为方程\(a=g(x)\)有\(n\)个解得问题。解法：用导数做出函数g(x)的大致图像，结合图像求解

曲线静，直线动，一静两动型〔两动同步型〕

例2已知函数\(f(x)=x^2+ax+1(a>0)\)，

(1).若\(f(x)\)的值域为\([0,+\infty)\)，求关于\(x\)的方程\(f(x)=4\)的解；

分析：题目已知\(f(x)\)的值域为\([0,+\infty)\)，其本质是为了告诉\(a\)的取值；

只有函数\(f(x)\)和\(x\)轴相切时，\(f(x)\)的值域才能为\([0,+\infty)\)，

故\(\Delta =a^2-4=0\)，解得\(a=2\)(舍去负值)，则需要求解方程\(x^2+2x+1=4\)

即求解\(x^2+2x-3=0\)，解得\(x=-3\)或\(x=1\)，故其解集为\(\{-3,1\}\)。

(2).当\(a=2\)时，函数\(g(x)=[f(x)]^2-2m\cdot f(x)+m^2-1\)在\([-2，1]\)上有三个零点，求\(m\)的取值范围；

分析：函数\(g(x)\)的零点，即方程\([f(x)]^2-2m\cdot f(x)+m^2-1=0\)的根，

而方程可以分解为\([f(x)-(m-1)][f(x)-(m+1)]=0\)，

故方程\(f(x)=m-1\)和方程\(f(x)=m+1\)在\(x\in [-2，1]\)上共有三个解；

在同一个坐标系中做出函数\(y=f(x)(x\in [-2，1])\)和直线\(y=m-1\)和\(y=m+1\)，如图所示，

当\(0<m-1\leqslant 1\)时，函数\(y=f(x)\)与直线\(y=m-1\)有两个交点；

同时\(m+1\in [2，3]\)，此时函数\(y=f(x)\)与直线\(y=m+1\)只有一个交点，满足题意；

故只需要由\(0<m-1\leqslant 1\)，解得\(m\in (1，2]\).

曲线静，直线动，一静两动型〔两动异步型〕

例3【2018广东中山期末】已知\(\cfrac{1}{3}\leq k<1\)，函数\(f(x)=|2^x-1|-k\)的零点分别为\(x_1\)、\(x_2\)，\((x_1<x_2)\)，函数\(g(x)=|2^x-1|-\cfrac{k}{2k+1}\)的零点分别为\(x_3\)、\(x_4\)，\((x_3<x_4)\)，则\(x_4+x_2-(x_3+x_1)\)的最小值为【】

分析：函数\(f(x)\)的零点问题，转化为函数\(y=|2^x-1|\)与\(y=k\)的图像交点的横坐标问题，

同理，函数\(g(x)\)的零点问题，转化为函数\(y=|2^x-1|\)与\(y=\cfrac{k}{2k+1}\)的图像交点的横坐标问题，

又由于\(y=\cfrac{k}{2k+1}=\cfrac{1}{2+\frac{1}{k}}\)，在\(k\in [\cfrac{1}{3}，1)\)上单调递增，

即当\(k\)的取值从\(\cfrac{1}{3}\)增大到\(1\)时，\(\cfrac{k}{2k+1}\)的取值对应的从\(\cfrac{1}{5}\)增大到\(\cfrac{1}{3}\)，

做出如下的图像，从图像入手分析，当\(y=k\)向上平移时，\(x_2-x_1\)逐渐增大，同理对应的\(x_4-x_3\)逐渐增大，

所以要使得\(x_4+x_2-(x_3+x_1)\)取到最小值，则需要\(x_4-x_3\)和\(x_2-x_1\)同时取到最小值，此时\(k=\cfrac{1}{3}\)，

同时对应的有\(\cfrac{k}{2k+1}=\cfrac{1}{5}\)；

此时，\(|2^{x_2}-1|=\cfrac{1}{3}\)，即\(2^{x_2}-1=\cfrac{1}{3}\)，解得\(x_2=log_2\cfrac{4}{3}\)，

又\(|2^{x_1}-1|=\cfrac{1}{3}\)，即\(1-2^{x_1}=\cfrac{1}{3}\)，解得\(x_1=log_2\cfrac{2}{3}\)，

同理对应的有\(|2^{x_4}-1|=\cfrac{1}{5}\)，即\(2^{x_4}-1=\cfrac{1}{5}\)，解得\(x_4=log_2\cfrac{6}{5}\)，

又\(|2^{x_3}-1|=\cfrac{1}{5}\)，即\(1-2^{x_3}=\cfrac{1}{5}\)，解得\(x_3=log_2\cfrac{4}{5}\)，

故此时\([x_4+x_2-(x_3+x_1)]_{min}=(log_2\cfrac{6}{5}-log_2\cfrac{4}{5})+(log_2\cfrac{4}{3}-log_2\cfrac{2}{3})=log_23\)，故选\(B\)。

解后反思：比如将条件更改为\(\cfrac{1}{3}\leq k\leq \cfrac{4}{5}\)，那么用相应的思路和方法，可以求解\(x_4+x_2-(x_3+x_1)\)的取值范围；

一曲线静，一曲线动，〔一静一动型〕

由$f(x)=k$型方程根的个数求参数的范围

原文：https://www.cnblogs.com/wanghai0666/p/12513893.html