平衡树入门

时间：2020-03-19 22:36:24 阅读：79 评论：0 收藏：0 [点我收藏+]

前置技能

平衡树是二叉搜索树的一种，二叉搜索树的定义如下：

空树是二叉搜索树
若二叉搜索树的左子树不为空，则其左子树上所有点的权值均小于其根节点的值
若二叉搜索树的右子树不为空，则其右子树上所有点的权值均大于其根节点的值
二叉搜索树的左右子树均为二叉搜索树

对于有$n$个节点的二叉搜索树，每次基本操作的最优复杂度为$O(logn)$，由于二叉搜索树可能退化成一条链，所以最坏复杂度$O(n)$

而每种平衡树都能通过一些方法让二叉搜索树不退化成一条链，每次操作的时间复杂度保持在$O(logn)$

平衡树主要分为两种：

有旋转的树：AVL树，Splay树，红黑树
无旋转的树：替罪羊树，fhq-Treap

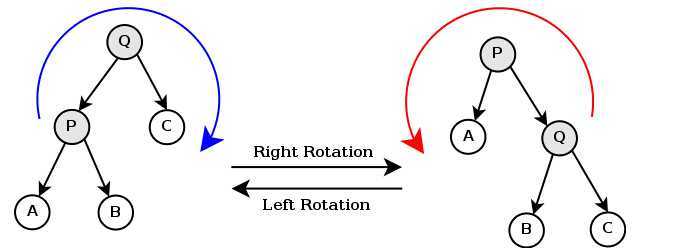
树旋转也分为两种：

右旋：将自己变为左孩子的右孩子，同时将左孩子的右孩子变为自己的左孩子
左旋：将自己变为右孩子的左孩子，同时将右孩子的左孩子变为自己的右孩子

技术分享图片

替罪羊树

替罪羊树通过重构来维持树的平衡，在插入、删除操作之后，从上到下检测途经的节点，若发现失衡，则将以该节点为根的子树重构

struct node {
    int l, r;   // 左右子树
    int val;    // 节点权值
    int sz;     // 包括已删除节点的子树大小
    int fsz;    // 实际大小，不包括已删除节点的子树大小
    int cnt;    // 数据出现的次数
};

替罪羊树的删除是一种惰性删除，只是打上一个标记表示该节点已经被删除，实际大小就是没有被打上标记的节点数量，这个标记就是cnt，cnt=0表示节点已经被删除，cnt>0是表示节点存在

为了判断节点是否需要重构，我们定义一个平衡因子$\alpha$(取值在0.5到1之间)，一般取0.75，当满足以下两个条件时表示该节点需要重构

左子树或者右子树的sz大于整个子树的sz * $\alpha$(左子树或者右子树太大导致整个子树不平衡)
整个子树被删除的节点数量大于整个子树的sz * 0.3(被删除的节点太多导致整个子树不平衡)

bool imbalance(int &now)
{
    if (max(tree[tree[now].l].sz, tree[tree[now].r].sz) > tree[now].sz * alpha) return true;
    if (tree[now].sz - tree[now].fsz > tree[now].sz * 0.3) return true;
    return false;
}

对于需要重构的节点，重构分为两步：

先中序遍历展开存入向量，注意只有当前节点存在时(cnt>0)才能够存入向量
分治建二叉树(每次取区间中点作为根，然后递归两边为左右子树建树)

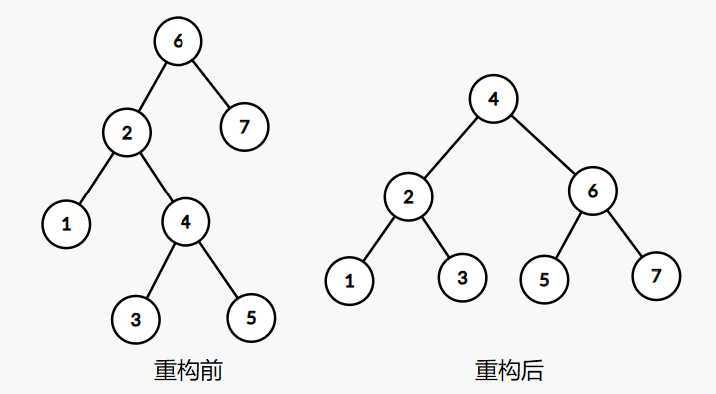
技术分享图片

在分治的同时，更新重构后子树每个节点的sz和fsz

void dfs(int &now)
{
    if (0 == now) return;
    dfs(tree[now].l);
    if (tree[now].cnt) v.push_back(now);
    dfs(tree[now].r);
}

void lift(int l, int r, int &now)
{
    if (l == r) {
        now = v[l];
        tree[now].l = tree[now].r = 0;
        tree[now].sz = tree[now].fsz = tree[now].cnt;
        return;
    }
    int mid = (l + r) / 2;
    now = v[mid];
    if (l < mid) lift(l, mid - 1, tree[now].l);
    else tree[now].l = 0;
    lift(mid + 1, r, tree[now].r);
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + tree[now].cnt;
    tree[now].fsz = tree[tree[now].l].fsz + tree[tree[now].r].fsz + tree[now].cnt;
}

void rebuild(int &now)
{
    v.clear();
    dfs(now);
    if (v.empty()) {
        now = 0;
        return;
    }
    lift(0, (int)v.size() - 1, now);
}

显然，对一颗重构后的子树，我们还需要从上向下采用头递归的方式(比较好写，自下而上需要多一个fa参数)更新路径上所有节点的sz和fsz

check函数表示检查now到end路径上所有的点，如果有不平衡的节点则重构以该节点为根的子树

注意：check函数是自上向下检查每个节点是否需要重构，因为如果自下而上判断，可能会导致重构很多次，复杂度不能保证，而自上向下判断只需要重构第一个不平衡的节点即可

void update(int &now, int end)
{
    if (now == end) return;
    if (tree[end].val < tree[now].val) update(tree[now].l, end);
    else update(tree[now].r, end);
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + tree[now].cnt;
    tree[now].fsz = tree[tree[now].l].fsz + tree[tree[now].r].fsz + tree[now].cnt;
}

void check(int &now, int end)
{
    if (now == end) return;
    if (imbalance(now)) {
        rebuild(now);
        update(root, now);
        return;
    }
    if (tree[end].val < tree[now].val) check(tree[now].l, end);
    else check(tree[now].r, end);
}

替罪羊的插入操作和普通二叉搜索树的插入操作差不多，只是在每次插入之后，都需要从根节点root到当前节点now自上向下判断每个节点是否需要重构

void insert(int &now, int val)
{
    if (0 == now) {
        newnode(now, val);
        check(root, now);
        return;
    }
    tree[now].sz++;
    tree[now].fsz++;
    if (val < tree[now].val) insert(tree[now].l, val);
    else if (val == tree[now].val) {
        tree[now].cnt++;
        check(root, now);
    }
    else insert(tree[now].r, val);
}

删除操作同理，每次删除后，从根节点root到当前节点now自上向下判断每个节点是否需要重构

注意：删除操作减少的是节点的fsz，不是节点sz，fsz表示的是真实的大小(不包括已经删除的节点)

void del(int &now, int val)
{
    if (tree[now].cnt && tree[now].val == val) {
        tree[now].cnt--;
        tree[now].fsz--;
        check(root, now);
        return;
    }
    tree[now].fsz--;
    if (val < tree[now].val) del(tree[now].l, val);
    else del(tree[now].r, val);
}

对于查询某个数的排名qrank(x)和查询某个排名上的数qnum(x)，则可以利用二叉搜索树的性质来求解

对于某个数的前驱，只需要查询qnum(qrank(x)-1)，即查询(这个数的排名-1)上的数

但对于后继，不能查询qnum(qrank(x)+1)，因为可能有重复的数字，比如说1 2 2 4，查询2的后继时，2的排名为2，但4的排名却是4，这样查询的结果依然是2，所以我们应该查询qnum(qrank(x+1))

例题：bzoj-3224普通平衡树

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>

using namespace std;

const int N = 100010;
const double alpha = 0.75;

struct node {
    int l, r, val;
    int sz, fsz, cnt;
};

node tree[N];
int root, cnt, n;
vector<int> v;

inline void newnode(int &now, int val)
{
    now = ++cnt;
    tree[now].val = val;
    tree[now].sz = tree[now].fsz = 1;
    tree[now].cnt = 1;
}

bool imbalance(int &now)
{
    if (max(tree[tree[now].l].sz, tree[tree[now].r].sz) > tree[now].sz * alpha) return true;
    if (tree[now].sz - tree[now].fsz > tree[now].sz * 0.3) return true;
    return false;
}

void dfs(int &now)
{
    if (0 == now) return;
    dfs(tree[now].l);
    if (tree[now].cnt) v.push_back(now);
    dfs(tree[now].r);
}

void lift(int l, int r, int &now)
{
    if (l == r) {
        now = v[l];
        tree[now].l = tree[now].r = 0;
        tree[now].sz = tree[now].fsz = tree[now].cnt;
        return;
    }
    int mid = (l + r) / 2;
    now = v[mid];
    if (l < mid) lift(l, mid - 1, tree[now].l);
    else tree[now].l = 0;
    lift(mid + 1, r, tree[now].r);
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + tree[now].cnt;
    tree[now].fsz = tree[tree[now].l].fsz + tree[tree[now].r].fsz + tree[now].cnt;
}

void rebuild(int &now)
{
    v.clear();
    dfs(now);
    if (v.empty()) {
        now = 0;
        return;
    }
    lift(0, (int)v.size() - 1, now);
}

void update(int &now, int end)
{
    if (now == end) return;
    if (tree[end].val < tree[now].val) update(tree[now].l, end);
    else update(tree[now].r, end);
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + tree[now].cnt;
    tree[now].fsz = tree[tree[now].l].fsz + tree[tree[now].r].fsz + tree[now].cnt;
}

void check(int &now, int end)
{
    if (now == end) return;
    if (imbalance(now)) {
        rebuild(now);
        update(root, now);
        return;
    }
    if (tree[end].val < tree[now].val) check(tree[now].l, end);
    else check(tree[now].r, end);
}

void insert(int &now, int val)
{
    if (0 == now) {
        newnode(now, val);
        check(root, now);
        return;
    }
    tree[now].sz++;
    tree[now].fsz++;
    if (val < tree[now].val) insert(tree[now].l, val);
    else if (val == tree[now].val) {
        tree[now].cnt++;
        check(root, now);
    }
    else insert(tree[now].r, val);
}

void del(int &now, int val)
{
    if (tree[now].cnt && tree[now].val == val) {
        tree[now].cnt--;
        tree[now].fsz--;
        check(root, now);
        return;
    }
    tree[now].fsz--;
    if (val < tree[now].val) del(tree[now].l, val);
    else del(tree[now].r, val);
}

int qrank(int val)
{
    int now = root, rank = 1;
    while (now) {
        if (val <= tree[now].val) now = tree[now].l;
        else {
            rank = rank + tree[tree[now].l].fsz + tree[now].cnt;
            now = tree[now].r;
        }
    }
    return rank;
}

int qnum(int rank)
{
    int now = root;
    while (now) {
        int lz = tree[tree[now].l].fsz;
        if (tree[now].cnt && rank >= lz + 1 && rank <= lz + tree[now].cnt) break;
        if (lz >= rank) now = tree[now].l;
        else {
            rank = rank - lz - tree[now].cnt;
            now = tree[now].r;
        }
    }
    return tree[now].val;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        int op, x;
        scanf("%d%d", &op, &x);
        if (1 == op) insert(root, x);
        else if (2 == op) del(root, x);
        else if (3 == op) printf("%d\n", qrank(x));
        else if (4 == op) printf("%d\n", qnum(x));
        else if (5 == op) printf("%d\n", qnum(qrank(x) - 1));
        else printf("%d\n", qnum(qrank(x + 1)));
    }
    return 0;
}

bzoj 3224

fhq-Treap

treap是单词tree和heap的组合，表明treap是一种由树和堆组成的数据结构，所以fhq-Treap的每个节点都必须存储val和key两个值，其中val表示节点权值，key是随机的一个值，val满足二叉搜索树的性质，而key满足堆的性质，由于key是随机的，所以treap是期望平衡的

struct node {
    int l, r;   // 左右子树
    int val;    // 节点权值
    int key;    // 随机的关键值
    int sz;     // 以该节点为根的子树大小
};

fhq-Treap只有两个基本操作：分裂split和合并merge

分裂分为两种：

按值val分裂：把树分裂成两棵树，其中一棵树上所有节点的权值都小于等于val，另一颗树上所有节点的权值都大于val
按大小分裂：把树分裂成两棵树，其中一棵树的大小等于给定的大小，其余的节点在另一棵树里

接下来我们以按值分裂为例，假设权值小于等于val的那一棵树的根节点为x，称为第一棵树，另一棵树的根节点为y，称为第二棵树

根据二叉搜索树的性质，如果当前节点now的权值小于等于val，那么当前节点now和now的左子树都属于第一棵树，然而now的右子树上的节点不一定都属于第一棵树，那么我们就继续递归分裂now的右子树，同理，如果当前节点now的权值大于val，那么当前节点now和now的右子树都属于第二棵树，然而now的左子树上的节点不一定都属于第二棵树，继续递归分裂now的左子树

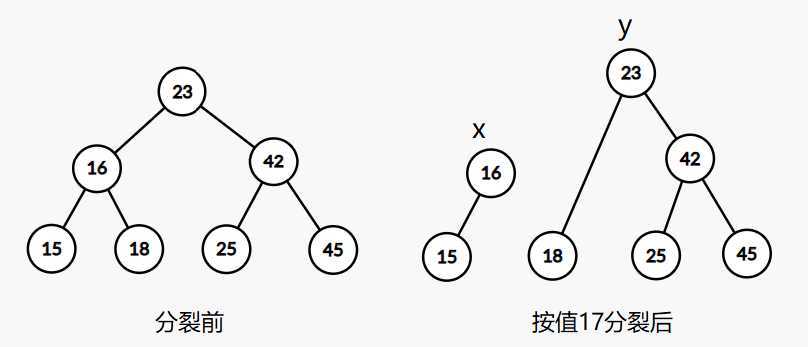
技术分享图片

注意：分裂的同时需要更新路径上节点的sz，x和y采用引用传递(比较好写)

inline void update(int now)
{
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + 1;
}

void split(int now, int val, int &x, int &y)
{
    if (0 == now) {
        x = y = 0;
        return;
    }
    if (tree[now].val <= val) {
        x = now;
        split(tree[now].r, val, tree[now].r, y);
    }
    else {
        y = now;
        split(tree[now].l, val, x, tree[now].l);
    }
    update(now);
}

合并时，以维护小根堆为例，有两种情况：

第一棵树根节点x的key值比第二棵树根节点y的key值小，由于第一棵树上节点的权值都小于第二棵树上节点的权值，那么根据二叉搜索树和小根堆的性质，第一棵树就在第二棵树的“左上方”，此时就递归合并节点x的右子树和节点y
第二棵树根节点x的key值比第二棵树根节点y的key值大，同理，那么第一棵树就在第二棵树的“左下方”，此时递归合并节点x和节点y的左子树

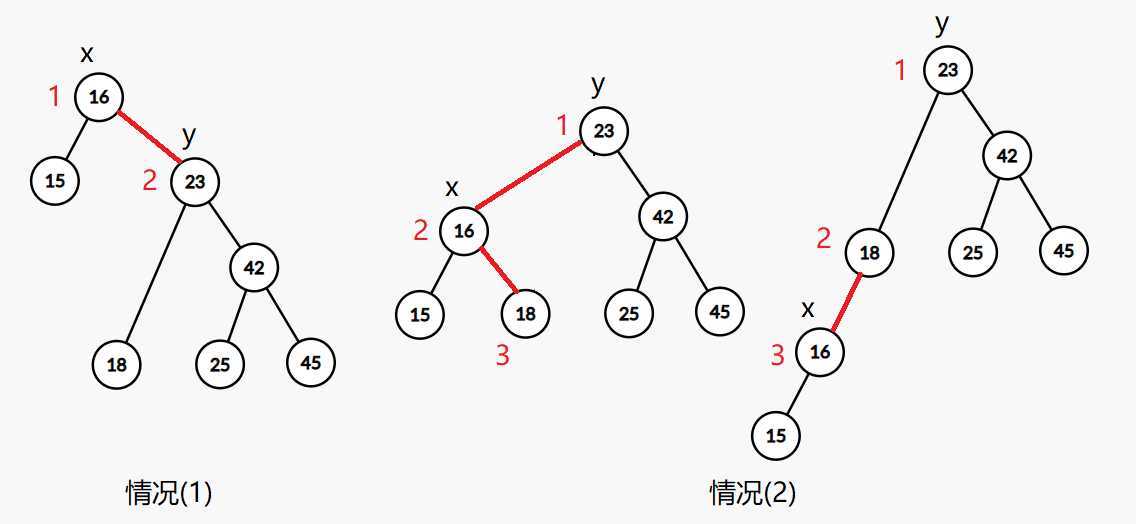
技术分享图片

merge(x,y)表示将以x为根的树和以y为根的树合并同时返回合并后的根节点

int merge(int x, int y)
{
    if (0 == x || 0 == y) return x + y;
    if (tree[x].key < tree[y].key) {
        tree[x].r = merge(tree[x].r, y);
        update(x);
        return x;
    }
    else {
        tree[y].l = merge(x, tree[y].l);
        update(y);
        return y;
    }
}

有了分裂split和合并merge操作之后，二叉搜索树的基本操作就能用这两个操作来表示出来，以插入操作为例，假设需要插入节点的值为val，我们先可以将树按val分裂成两棵树，再将第一棵树，新节点，第二棵树按照顺序依次合并成一棵树

inline void insert(int val)
{
    int x, y;
    split(root, val, x, y);
    root = merge(merge(x, newnode(val)), y);
}

例题：bzoj-3224普通平衡树

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <stdlib.h>

using namespace std;

const int N = 100010;
const int M = 1000;

struct node {
    int l, r;
    int val, key, sz;
};

node tree[N];
int cnt, root, t;

inline int newnode(int val)
{
    tree[++cnt].val = val;
    tree[cnt].key = rand() % M;
    tree[cnt].sz = 1;
    return cnt;
}

inline void update(int now)
{
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + 1;
}

void split(int now, int val, int &x, int &y)
{
    if (0 == now) {
        x = y = 0;
        return;
    }
    if (tree[now].val <= val) {
        x = now;
        split(tree[now].r, val, tree[now].r, y);
    }
    else {
        y = now;
        split(tree[now].l, val, x, tree[now].l);
    }
    update(now);
}

int merge(int x, int y)
{
    if (0 == x || 0 == y) return x + y;
    if (tree[x].key < tree[y].key) {
        tree[x].r = merge(tree[x].r, y);
        update(x);
        return x;
    }
    else {
        tree[y].l = merge(x, tree[y].l);
        update(y);
        return y;
    }
}

inline void insert(int val)
{
    int x, y;
    split(root, val, x, y);
    root = merge(merge(x, newnode(val)), y);
}

inline void del(int val)
{
    int x, y, z;
    split(root, val, x, z);
    split(x, val - 1, x, y);
    y = merge(tree[y].l, tree[y].r);
    root = merge(merge(x, y), z);
}

inline int qr(int val)
{
    int x, y;
    split(root, val - 1, x, y);
    int res = tree[x].sz + 1;
    root = merge(x, y);
    return res;
}

inline int qn(int rank)
{
    int now = root;
    while (now) {
        if (tree[tree[now].l].sz + 1 == rank) break;
        else if (tree[tree[now].l].sz >= rank)
            now = tree[now].l;
        else {
            rank = rank - tree[tree[now].l].sz - 1;
            now = tree[now].r;
        }
    }
    return tree[now].val;
}

inline int pre(int val)
{
    int x, y;
    split(root, val - 1, x, y);
    int now = x;
    while (tree[now].r) now = tree[now].r;
    int res = tree[now].val;
    root = merge(x, y);
    return res;
}

inline int nex(int val)
{
    int x, y;
    split(root, val, x, y);
    int now = y;
    while (tree[now].l) now = tree[now].l;
    int res = tree[now].val;
    root = merge(x, y);
    return res;
}

int main()
{
    scanf("%d", &t);
    while (t--) {
        int opt, x;
        scanf("%d%d", &opt, &x);
        if (1 == opt) insert(x);
        if (2 == opt) del(x);
        if (3 == opt) printf("%d\n", qr(x));
        if (4 == opt) printf("%d\n", qn(x));
        if (5 == opt) printf("%d\n", pre(x));
        if (6 == opt) printf("%d\n", nex(x));
    }
    return 0;
}

bzoj 3224

fhq-Treap还可以对区间信息进行维护，包括区间反转，区间交换等等，这时就需要按大小进行分裂，fhq-Treap对区间[l,r]操作的核心思想仍然是分裂，将区间[l,r]直接从树中分裂出来

fhq-Treap对区间的操作和线段树类似，需要维护一个懒标记，当进行分裂和合并时需要下传懒标记

此时fhq-Treap仍然用随机的关键值key维护堆的性质，但不再用节点的权值维护二叉树的性质，而是用该点在序列中的位置来维护二叉树的性质，显然对这棵树中序遍历一遍就可以得到原序列

注意：这个“该点在序列中的位置”并不会体现在代码中，在分裂时而是通过当前节点now左子树的大小与需要分裂的大小sz的大小关系来决定是向左子树移动还是向右子树移动

分裂时，如果当前节点now左子树的大小小于还需要分裂的大小sz，那么当前节点now和now的左子树都应该属于第一棵树，同时递归分裂now的右子树，此时还需要分裂的大小sz应该减去刚刚分裂出的树的大小(now左子树的大小+1)，同理，如果前节点now左子树的大小大于等于还需要分裂的大小sz，则应该递归分裂now的左子树

由于这棵树是按该点在序列中的位置来维护二叉树性质的，所以分裂后第一棵树表示的区间就是[1,sz]，其他节点在第二棵树上

void split(int now, int sz, int &x, int &y)
{
    if (0 == now) x = y = 0;
    else {
        pushdown(now);
        if (tree[tree[now].l].sz < sz) {
            x = now;
            split(tree[now].r, sz - tree[tree[now].l].sz - 1, tree[now].r, y);
        }
        else {
            y = now;
            split(tree[now].l, sz, x, tree[now].l);
        }
        update(now);
    }
}

因为仍然使用关键值key维护fhq-Treap堆的性质，所以合并merge和按值分裂只多了把懒标记向下传递的过程

int merge(int x, int y)
{
    if (0 == x || 0 == y) return x + y;
    if (tree[x].key < tree[y].key) {
        pushdown(x);
        tree[x].r = merge(tree[x].r, y);
        update(x);
        return x;
    }
    else {
        pushdown(y);
        tree[y].l = merge(x, tree[y].l);
        update(y);
        return y;
    }
}

有了分裂split和合并merge操作之后，对于区间[l,r]，可以先分裂出[1,r]区间，再将区间[1,r]分裂为[1,l-1]和[l,r]两个区间

例题：poj-3580 SuperMemo

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <stdlib.h>

using namespace std;

const int N = 200010;
const int M = 1000;
const int INF = 0x3f3f3f3f;

struct node {
    int l, r, key, sz, rev;
    int val, imin, lz;
};

node tree[N];
int cnt, root, t, n, m;
char s[M];

void flip(int x)
{
    swap(tree[x].l, tree[x].r);
    tree[tree[x].l].rev ^= 1;
    tree[tree[x].r].rev ^= 1;
    tree[x].rev = 0;
}

void add(int x, int val)
{
    if (0 == x) return;
    tree[x].val += val;
    tree[x].imin += val;
    tree[x].lz += val;
}

void update(int x)
{
    tree[x].sz = tree[tree[x].l].sz + tree[tree[x].r].sz + 1;
    tree[x].imin = min(tree[x].val, min(tree[tree[x].l].imin, tree[tree[x].r].imin));
}

void pushdown(int x)
{
    if (tree[x].rev) flip(x);
    if (tree[x].lz) {
        add(tree[x].l, tree[x].lz);
        add(tree[x].r, tree[x].lz);
        tree[x].lz = 0;
    }
}

int newnode(int val)
{
    tree[++cnt].val = val;
    tree[cnt].imin = val;
    tree[cnt].key = rand() % M;
    tree[cnt].sz = 1;
    return cnt;
}

void split(int now, int sz, int &x, int &y)
{
    if (0 == now) x = y = 0;
    else {
        pushdown(now);
        if (tree[tree[now].l].sz < sz) {
            x = now;
            split(tree[now].r, sz - tree[tree[now].l].sz - 1, tree[now].r, y);
        }
        else {
            y = now;
            split(tree[now].l, sz, x, tree[now].l);
        }
        update(now);
    }
}

int merge(int x, int y)
{
    if (0 == x || 0 == y) return x + y;
    if (tree[x].key < tree[y].key) {
        pushdown(x);
        tree[x].r = merge(tree[x].r, y);
        update(x);
        return x;
    }
    else {
        pushdown(y);
        tree[y].l = merge(x, tree[y].l);
        update(y);
        return y;
    }
}

void insert(int k, int val)
{
    int x, y;
    split(root, k, x, y);
    root = merge(merge(x, newnode(val)), y);
}

void del(int k)
{
    int x, y, z;
    split(root, k - 1, x, y);
    split(y, 1, y, z);
    root = merge(x, z);
}

int qimin(int l, int r)
{
    int x, y, z;
    split(root, r, x, z);
    split(x, l - 1, x, y);
    int res = tree[y].imin;
    root = merge(x, merge(y, z));
    return res;
}

void qadd(int l, int r, int val)
{
    int x, y, z;
    split(root, r, x, z);
    split(x, l - 1, x, y);
    add(y, val);
    root = merge(x, merge(y, z));
}

void qreverse(int l, int r)
{
    int x, y, z;
    split(root, r, x, z);
    split(x, l - 1, x, y);
    tree[y].rev ^= 1;
    root = merge(x, merge(y, z));
}

void qrevolve(int l, int r, int len)
{
    len %= (r - l + 1);
    if (0 == len) return;
    int x, y, z, k;
    split(root, r, x, k);
    split(x, l - 1, x, y);
    split(y, r - l + 1 - len, y, z);
    root = merge(x, merge(merge(z, y), k));
}

int main()
{
    tree[0].val = tree[0].imin = INF;
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        int val;
        scanf("%d", &val);
        root = merge(root, newnode(val));
    }
    scanf("%d", &m);
    while (m--) {
        scanf("%s", s + 1);
        int l, r, k, val;
        if (‘A‘ == s[1]) {
            scanf("%d%d%d", &l, &r, &val);
            qadd(l, r, val);
        }
        else if (‘R‘ == s[1] && ‘E‘ == s[4]) {
            scanf("%d%d", &l, &r);
            qreverse(l, r);
        }
        else if (‘R‘ == s[1] && ‘O‘ == s[4]) {
            scanf("%d%d%d", &l, &r, &k);
            qrevolve(l, r, k);
        }
        else if (‘I‘ == s[1]) {
            scanf("%d%d", &l, &val);
            insert(l, val);
        }
        else if (‘D‘ == s[1]) {
            scanf("%d", &l);
            del(l);
        }
        else {
            scanf("%d%d", &l, &r);
            printf("%d\n", qimin(l, r));
        }
    }
    return 0;
}

poj 3580

fhq-Treap最大的缺点就是常数很大，有时候会被卡，Splay常数小，不容易被卡

AVL树

AVL树为了维持树的平衡，引入了平衡因子BF的概念，平衡因子=左子树树高-右子树树高(右子树树高-左子树树高)

struct node {
    int l, r;   // 左右子树
    int val;    // 节点权值
    int h;      // 树高
    int sz;     // 以该节点为根的子树大小
};

AVL树中每个节点的平衡因子只能为-1，0或1，当某个节点的平衡因子过大或者过小时，则通过树旋转的方式来让树恢复平衡，显然AVL树的树高为$O(logn)$，每次操作的时间复杂度为$O(logn)$

向一棵平衡的AVL数中插入或者删除一个节点，在没有调整前，树中每个节点平衡因子的取值只能为-2，-1，0，1或2

那么以下四种情况需要调整：

LL：在当前节点now左子树的左子树上插入节点导致树不平衡，此时now的BF>1，now左子树的BF>0(插入之前可能为0或者1)，右旋当前节点now使树平衡
LR：在当前节点now左子树的右子树上插入节点导致树不平衡，此时now的BF>1，而now右子树的BF<=0(插入之前可能为1，0，-1)，先左旋now的左子树，再右旋当前节点使树平衡
RL：在当前节点now右子树的左子树上插入节点导致树不平衡，先右旋now的右子树，再左旋当前节点使树平衡
RR：在当前节点now右子树的右子树上插入节点导致树不平衡，左旋当前节点 now使树平衡

旋转之后需要更新当前节点now和now左右子树的大小、树高

zag表示左旋，zig表示右旋，check检查当前节点now是否平衡

inline int calc(int now)
{
    return tree[tree[now].l].h - tree[tree[now].r].h;
}

inline void zag(int &now)
{
    int r = tree[now].r;
    tree[now].r = tree[r].l;
    tree[r].l = now;
    now = r;
    update(tree[now].l);
    update(now);
}

inline void zig(int &now)
{
    int l = tree[now].l;
    tree[now].l = tree[l].r;
    tree[l].r = now;
    now = l;
    update(tree[now].r);
    update(now);
}

inline void check(int &now)
{
    int nf = calc(now);
    if (nf > 1) {
        int lf = calc(tree[now].l);
        if (lf > 0) zig(now);
        else {
            zag(tree[now].l);
            zig(now);
        }
    }
    else if (nf < -1) {
        int rf = calc(tree[now].r);
        if (rf < 0) zag(now);
        else {
            zig(tree[now].r);
            zag(now);
        }
    }
    else if (now) update(now);
}

AVL的插入操作和二叉搜索树几乎没有区别，只是在插入后，自下而上回溯检查路径上的节点是否平衡，所以采用头递归的方式插入

对于删除操作，如果需要删除的节点只有一个儿子节点或者没有儿子节点，那么直接删除就可以了，对于有双儿子的节点，AVL树有两种删除方法：

将需要删除的节点旋转到叶子节点，直接删除即可
先找到需要删除节点的后继节点，用后继节点代替自己的位置，由于后继节点一定没有左儿子，所以后继节点直接删除即可

无论哪种方法，同样在删除后，需要自下而上回溯检查路径上的节点是否平衡

查询某个数的排名qrank(x)和查询某个排名上的数qnum(x)和替罪羊树差不多，只是替罪羊树每个节点可能是多个相同的数，而AVL每个节点都只表示一个数

例题：bzoj-3224普通平衡树

#include <iostream>
#include <algorithm>
#include <cstdio>

using namespace std;

const int N = 100010;

struct node {
    int l, r, val;
    int h, sz;  
};

node tree[N];
int cnt, root, n;

inline void newnode(int &now, int val)
{
    now = ++cnt;
    tree[now].val = val;
    tree[now].sz = 1;
}

inline void update(int now)
{
    tree[now].sz = tree[tree[now].l].sz + tree[tree[now].r].sz + 1;
    tree[now].h = max(tree[tree[now].l].h, tree[tree[now].r].h) + 1;
}

inline int calc(int now)
{
    return tree[tree[now].l].h - tree[tree[now].r].h;
}

inline void zag(int &now)
{
    int r = tree[now].r;
    tree[now].r = tree[r].l;
    tree[r].l = now;
    now = r;
    update(tree[now].l);
    update(now);
}

inline void zig(int &now)
{
    int l = tree[now].l;
    tree[now].l = tree[l].r;
    tree[l].r = now;
    now = l;
    update(tree[now].r);
    update(now);
}

inline void check(int &now)
{
    int nf = calc(now);
    if (nf > 1) {
        int lf = calc(tree[now].l);
        if (lf > 0) zig(now);
        else {
            zag(tree[now].l);
            zig(now);
        }
    }
    else if (nf < -1) {
        int rf = calc(tree[now].r);
        if (rf < 0) zag(now);
        else {
            zig(tree[now].r);
            zag(now);
        }
    }
    else if (now) update(now);
}

void insert(int &now, int val)
{
    if (0 == now) newnode(now, val);
    else if (val < tree[now].val) insert(tree[now].l, val);
    else insert(tree[now].r, val);
    check(now);
}

int find(int &now, int fa)
{
    int res = 0;
    if (0 == tree[now].l) {
        res = now;
        tree[fa].l = tree[now].r;
    }
    else {
        res = find(tree[now].l, now);
        check(now);
    }
    return res;
}

void del(int &now, int val)
{
    if (val == tree[now].val) {
        int l = tree[now].l, r = tree[now].r;
        if (0 == l || 0 == r) now = l + r;
        else {
            now = find(r, r);
            if (now != r) tree[now].r = r;
            tree[now].l = l;
        }
    }
    else if (val < tree[now].val) del(tree[now].l, val);
    else del(tree[now].r, val);
    check(now);
}

int qrank(int val)
{
    int now = root, rank = 1;
    while (now) {
        if (val <= tree[now].val) now = tree[now].l;
        else {
            rank = rank + tree[tree[now].l].sz + 1;
            now = tree[now].r;
        }
    }
    return rank;
}

int qnum(int rank)
{
    int now = root;
    while (now) {
        if (tree[tree[now].l].sz + 1 == rank) break;
        else if (tree[tree[now].l].sz >= rank) now = tree[now].l;
        else {
            rank = rank - tree[tree[now].l].sz - 1;
            now = tree[now].r;
        }
    }
    return tree[now].val;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        int op, x;
        scanf("%d%d", &op, &x);
        if (1 == op) insert(root, x);
        else if (2 == op) del(root, x);
        else if (3 == op) printf("%d\n", qrank(x));
        else if (4 == op) printf("%d\n", qnum(x));
        else if (5 == op) printf("%d\n", qnum(qrank(x) - 1));
        else printf("%d\n", qnum(qrank(x + 1)));
    }
    return 0;
}

bzoj 3224

Splay

在Splay上一系列操作都基于伸展操作，伸展操作能够让出现频率(包括查询，插入，删除)较高的元素能够更靠近根节点，从而使查询、插入、删除整体的时间的变少

struct node {
    int l, r;   // 左右子树
    int val;    // 节点权值
    int sz;     // 以该节点为根的子树大小
    int cnt;    // 数据出现的次数
};

Splay在每次操作后，一般把节点伸展到根节点处，而伸展操作又是通过左旋和右旋来实现的，分为以下六种情况，每种情况都是将x节点伸展到根节点处

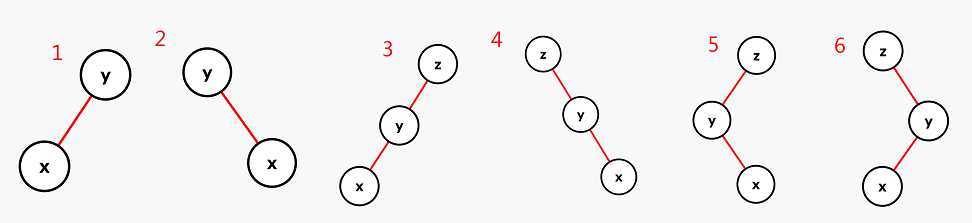
技术分享图片

情况1：对y右旋就可以将x节点伸展到根节点处，称为zig

情况2：对y左旋就可以将x节点伸展到根节点处，称为zag

情况3：先对节点z右旋，再对节点y右旋即可，称为zig-zig

情况4：与情况3相反，先对节点左旋，再对节点y左旋即可，称为zag-zag

情况5：先左旋节点y，再右旋节点z即可，称为zag-zig

情况6：与情况5相反，先右旋节点y，再左旋节点z，称为zig-zag

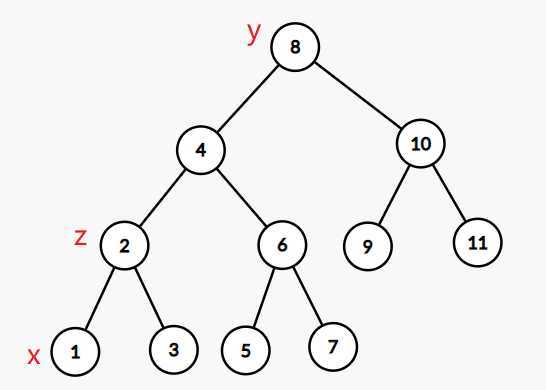
技术分享图片

如果需要将x节点伸展到y节点处，我们只需要递归把x节点伸展到z节点处，然后按照情况3处理即可

void splaying(int x, int &y)
{
    if (x == y) return;
    int &l = spl[y].l, &r = spl[y].r;
    if (x == l) zig(y);
    else if (x == r) zag(y);
    else {
        if (spl[x].val < spl[y].val) {
            if(spl[x].val < spl[l].val) {
                splaying(x, spl[l].l);
                zig(y), zig(y);
            }
            else {
                splaying(x, spl[l].r);
                zag(l), zig(y);
            }
        }
        else {
            if (spl[x].val > spl[r].val) {
                splaying(x, spl[r].r);
                zag(y), zag(y);
            }
            else {
                splaying(x, spl[r].l);
                zig(r), zag(y);
            }
        }
    }
}

注意：zig、zag函数的参数是引用传递，旋转后节点会发生改变，所以情况3执行的是zig(y)，zig(y)，splaying函数递归的出口是情况1和情况2

splay的插入操作和二叉树的插入操作差不多，插入后，将新插入的节点旋转到根节点即可

对于删除操作，splay则是先把需要删除的节点now伸展到根节点，找到节点now的后继节点，将后继节点伸展为根节点的右儿子，显然被伸展过的后继节点没有左儿子，此时我们只需要将后继节点的左儿子指向根节点的左儿子，将根节点指向这个后继节点即可，删除后需要更新根节点的sz

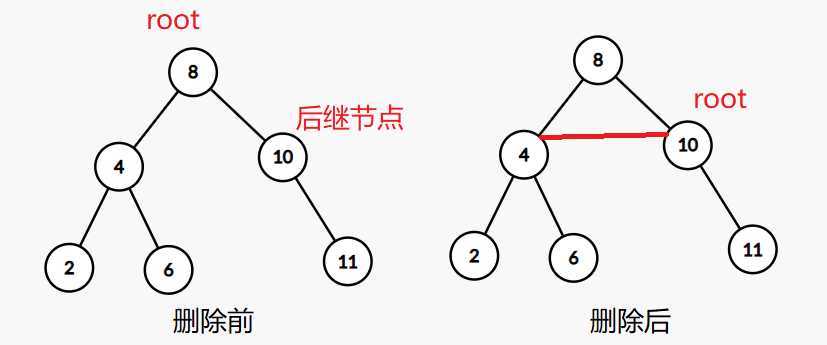
技术分享图片

查询某个数的排名qrank(x)和查询某个排名上的数qnum(x)和替罪羊树差不多，只是在查询之后，需要将查询到的节点伸展到根节点

例题：bzoj-3224普通平衡树

#include <iostream>
#include <algorithm>
#include <cstdio>

using namespace std;

const int N = 100010;

struct node {
    int l, r, val;
    int sz, cnt;
};

node spl[N];
int cnt, root, n;

inline void newnode(int &now, int val)
{
    now = ++cnt;
    spl[now].val = val;
    spl[now].sz++;
    spl[now].cnt++;
}

inline void update(int now)
{
    spl[now].sz = spl[spl[now].l].sz + spl[spl[now].r].sz + spl[now].cnt;
}

inline void zig(int &now)
{
    int l = spl[now].l;
    spl[now].l = spl[l].r;
    spl[l].r = now;
    now = l;
    update(spl[now].r);
    update(now);
}
inline void zag(int &now)
{
    int r = spl[now].r;
    spl[now].r = spl[r].l;
    spl[r].l = now;
    now = r;
    update(spl[now].l);
    update(now);
}

void splaying(int x, int &y)
{
    if (x == y) return;
    int &l = spl[y].l, &r = spl[y].r;
    if (x == l) zig(y);
    else if (x == r) zag(y);
    else {
        if (spl[x].val < spl[y].val) {
            if(spl[x].val < spl[l].val) {
                splaying(x, spl[l].l);
                zig(y), zig(y);
            }
            else {
                splaying(x, spl[l].r);
                zag(l), zig(y);
            }
        }
        else {
            if (spl[x].val > spl[r].val) {
                splaying(x, spl[r].r);
                zag(y), zag(y);
            }
            else {
                splaying(x, spl[r].l);
                zig(r), zag(y);
            }
        }
    }
}

inline void delnode(int now)
{
    splaying(now, root);
    if (spl[now].cnt > 1) {
        spl[now].sz--;
        spl[now].cnt--;
    }
    else if (spl[root].r) {
        int p = spl[root].r;
        while (spl[p].l) p = spl[p].l;
        splaying(p, spl[root].r);
        spl[spl[root].r].l = spl[root].l;
        root = spl[root].r;
        update(root);
    }
    else root = spl[root].l;
}

void insert(int &now, int val)
{
    if (0 == now) {
        newnode(now, val);
        splaying(now, root);
    }
    else if (val < spl[now].val) insert(spl[now].l, val);
    else if (val > spl[now].val) insert(spl[now].r, val);
    else {
        spl[now].sz++;
        spl[now].cnt++;
        splaying(now, root);
    }
}

void del(int now, int &val)
{
    if (spl[now].val == val) delnode(now);
    else if (val < spl[now].val) del(spl[now].l, val);
    else del(spl[now].r, val);
}

int qrank(int val)
{
    int now = root, rank = 1;
    while (now) {
        if (spl[now].val == val) {
            rank += spl[spl[now].l].sz;
            splaying(now, root);
            break;
        }
        if (val <= spl[now].val) now = spl[now].l;
        else {
            rank = rank + spl[spl[now].l].sz + spl[now].cnt;
            now = spl[now].r;
        }
    }
    return rank;
}

int qnum(int rank)
{
    int now = root;
    while (now) {
        int lz = spl[spl[now].l].sz;
        if (lz + 1 <= rank && rank <= lz + spl[now].cnt) {
            splaying(now, root);
            break;
        }
        else if (lz >= rank) now = spl[now].l;
        else {
            rank = rank - lz - spl[now].cnt;
            now = spl[now].r;
        }
    }
    return spl[now].val;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        int op, x;
        scanf("%d%d", &op, &x);
        if (1 == op) insert(root, x);
        else if (2 == op) del(root, x);
        else if (3 == op) printf("%d\n", qrank(x));
        else if (4 == op) printf("%d\n", qnum(x));
        else if (5 == op) printf("%d\n", qnum(qrank(x) - 1));
        else printf("%d\n", qnum(qrank(x + 1)));
    }
    return 0;
}

bzoj 3224

平衡树入门

原文：https://www.cnblogs.com/zzzzzzy/p/12509249.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)