参考url:
https://jakevdp.github.io/PythonDataScienceHandbook/05.09-principal-component-analysis.html
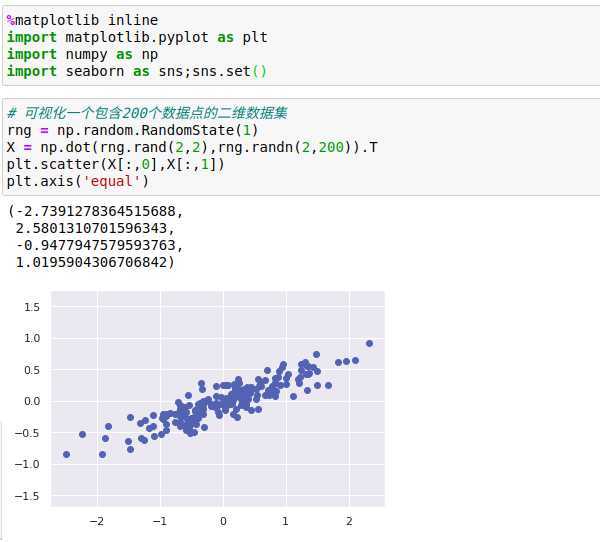
主成分分析(principal component analysis,PCA),无监督算法之一,PCA是一种非常基础的降维算法,适用于数据可视化、噪音过滤、特征抽取和特征工程等领域。
主成分分析是一个快速灵活的数据降维无监督方法。
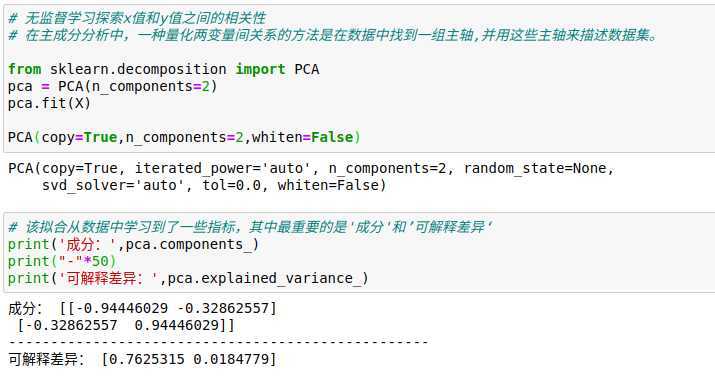
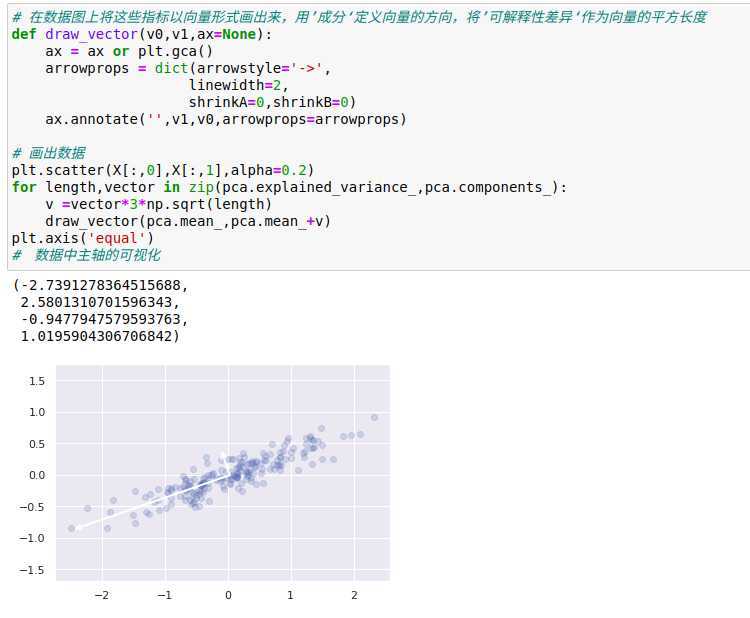
这些向量表示数据主轴,箭头长度表示输入数据中各个轴的‘重要程度’ ,即它衡量了数据投影到主轴上的方差的大小。每个数据点在主轴上的投影就是数据的‘主成分’。
将原始数据和这些主成分都画出来,将得到‘数据主轴的变换’图所示的结果。
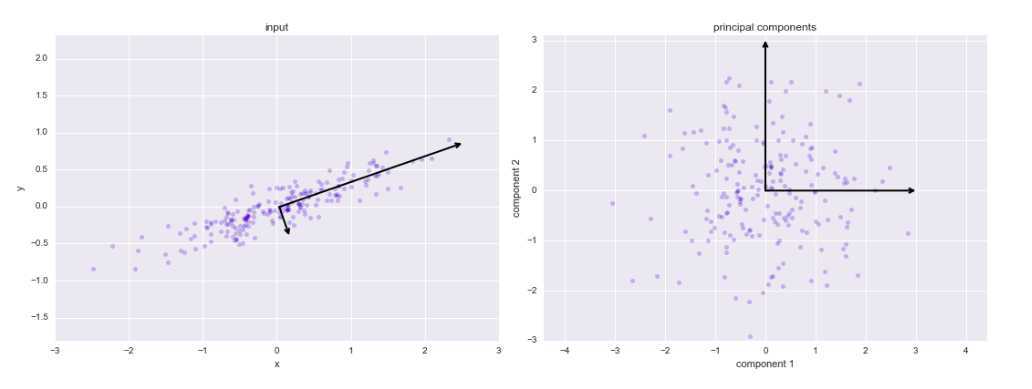
这种从数据的坐标轴变换到主轴的变换是一个仿射变换,仿射变换包含平移(translation)、旋转(rotation)和均匀缩放(uniform scaling)三个步骤。
用PCA降维意味着去除一个或多个最小主成分,从而得到一个更低维度且保留最大数据方差的数据投影。
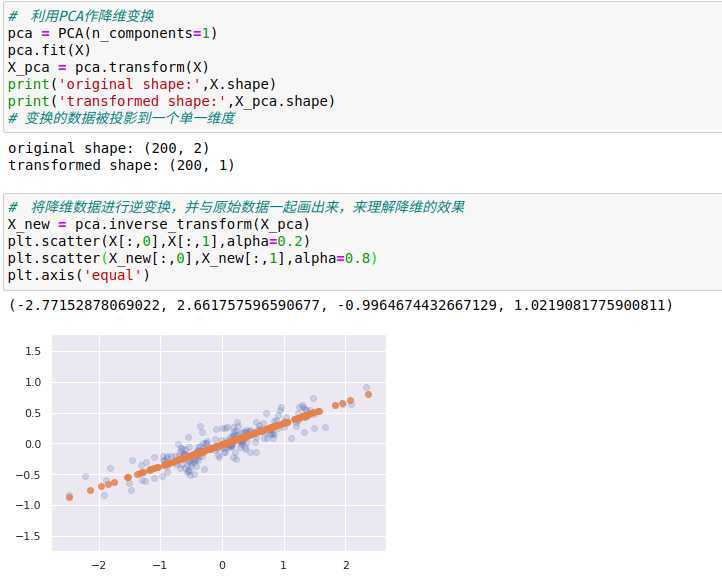
浅色的点是原始数据,深色的点是投影的版本。
PCA降维的含义:沿着最不重要的主轴的信息都被去除了,仅留下了含有最高方差值的数据成分,被去除的那一小部分方差值基本可以看成是数据在降维后损失的‘信息’量。
这种降维后的数据集在某种程度上足以体现出数据中最主要的关系:虽然有50%的数据维度被削减,但数据的总体关系仍然被大致保留了下来。
2、用PCA作数据可视化:手写数字
降维的有用之处在数据仅有两个维度时可能不是很明显,但是当数据维度很高时,它的价值就有所体现了。
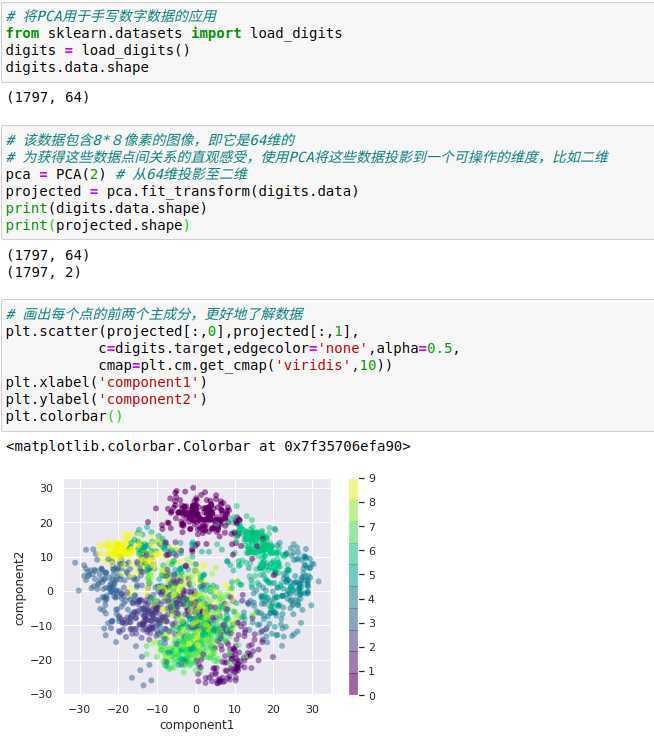
整个数据是一个64维的点云,而且这些点还是每个数据点沿着最大方差方向的投影。
从基向量的组合角度来理解这个问题。
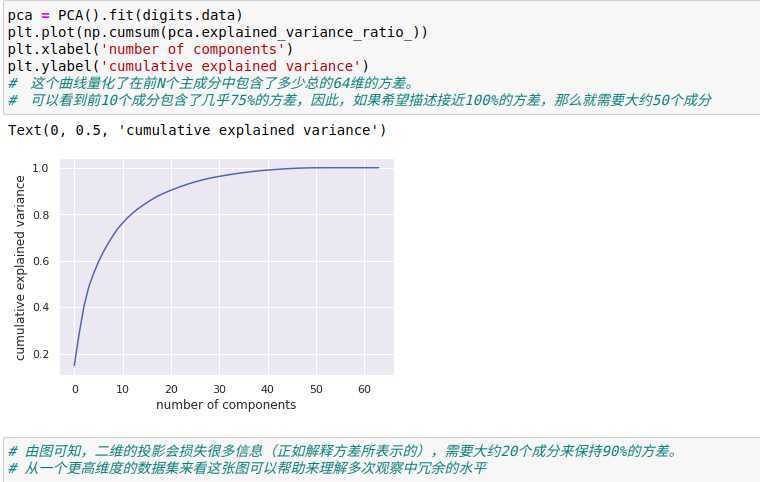
在实际使用PCA的过程中,正确估计用于描述数据的成分的数量是非常重要的环节,可以将累计方差贡献率看作是关于成分数量的函数,从而确定所需成分的数量。
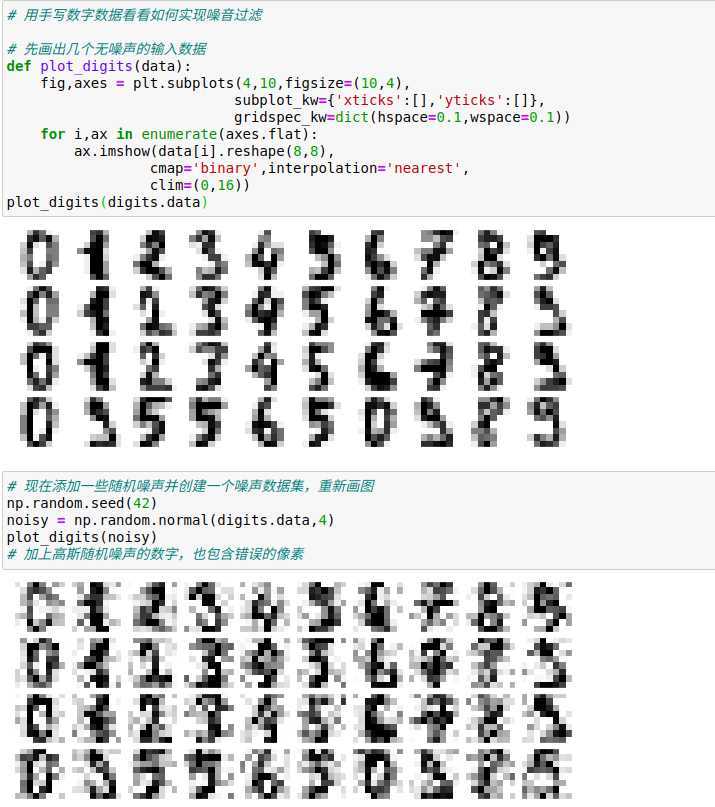
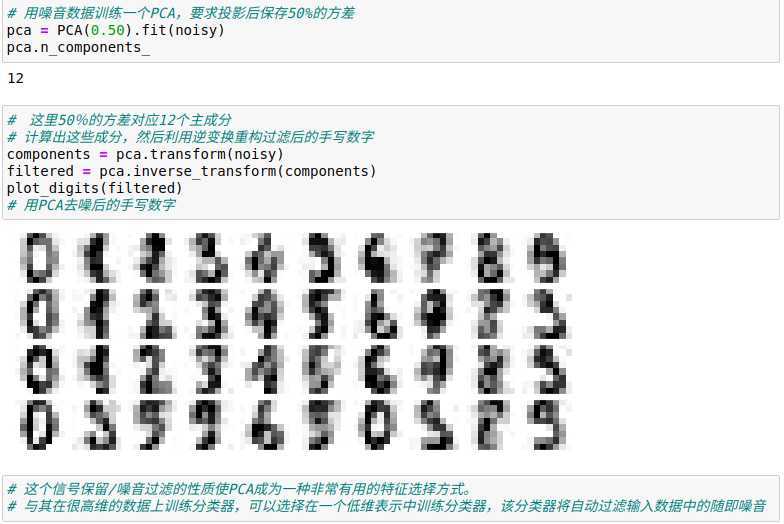
PCA也可以被用作噪声数据的过滤方法——任何成分的方差都远大于噪音的方差,所以相比于噪音,成分应该相对不受影响,因此如果仅用主成分的最大子集重构该数据,那么应该可以实现选择性保留信号并丢弃噪声。
原文:https://www.cnblogs.com/nuochengze/p/12535797.html