地址:http://codeforces.com/contest/1326
题意:给定n,输出一个长度为n的数字,满足以下条件:1:>0 2:各个位上不出现0 3:不能整除自己的任意一位。
解析:被这题给坑了一下。想不通我的33......7为什么不行,可能太长的话有被7整除的危险,并不能保证万无一失。所以我们需要一个能保证万无一失的通用方法。一个是2333.....3,或是5333.......3。
#include<iostream> #include<cstdio> #include<cstring> using namespace std; typedef long long ll; const int maxn=1e5+10; int a[maxn]; int main() { int t; cin>>t; while(t--) { int n; cin>>n; if(n==1) cout<<"-1"<<endl; else { cout<<"2"; for(int i=1;i<n;i++) cout<<"3"; cout<<endl; } } }

题意:有点小绕,大致就是我画的这个意思。

很明显,题意中有讲,x1=0固定。则a1=b1,直接规定maxx=a1,用这个maxx来维护数组a[]的i-1之前的最大值。ai=bi+maxx,然后更新maxx=max(maxx,bi+maxx);这个顺序不要错。
#include<iostream> #include<cstdio> #include<cstring> using namespace std; typedef long long ll; const int maxn=2e5+10; ll b[maxn]; ll a[maxn]; int main() { int n; cin>>n; for(int i=1;i<=n;i++) cin>>b[i]; int x; a[1]=b[1]; ll maxx=a[1]; for(int i=2;i<=n;i++) { a[i]=b[i]+maxx; maxx=max(maxx,b[i]+maxx); } for(int i=1;i<=n;i++) { if(i<n) cout<<a[i]<<" "; else cout<<a[i]<<endl; } }


题意:也是绕的一批,我这个英语渣压根就没看懂,靠队友才搞懂。
就是更定一个数量n的数组以及一个k,对这个数组进行分块,{|...|,|...|}k是多少,大括号里面就有几个|...|集合,里面是L,R,均为下标。集合之间不能有重叠,要保证全覆盖数组。可以把每个|...|里的最大值提出来,k个最大值相加,得到一个数。目的是找出这个最大数来,以及可以弄出这个数的分块方式有几种。
解析:既然是k个集合,那么要想保证各个最大值加起来最大,那么就要把前k个大的数做为每个集合里的最大值。以此为基准进行分块操作。再画个图看看:假设k=3
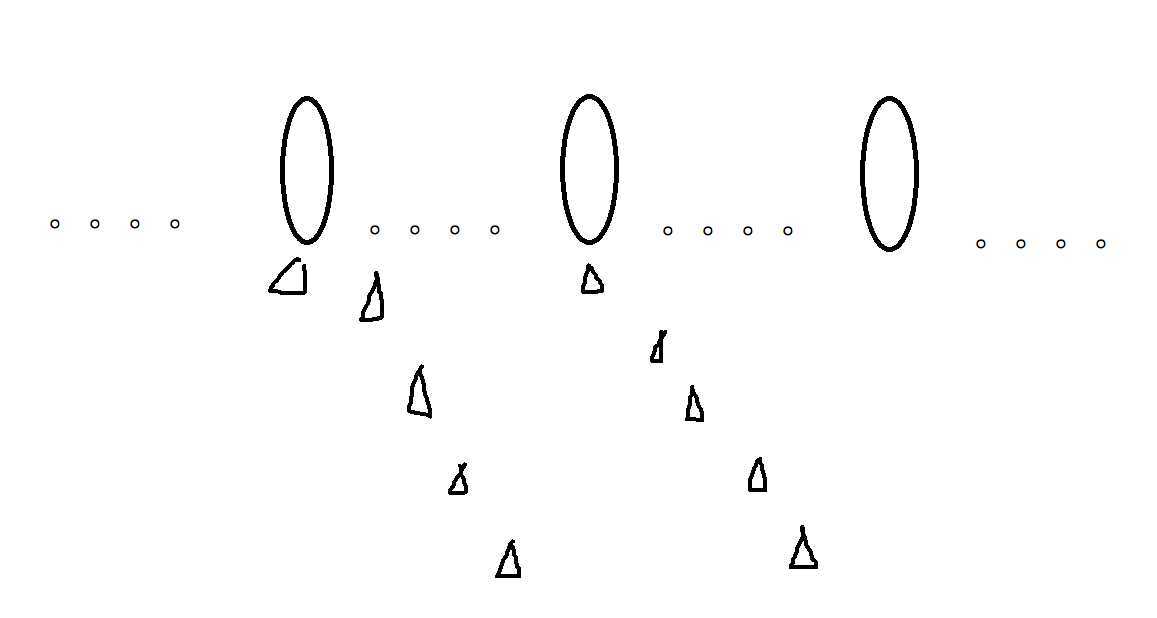
三角号表示分界线可放的地方,是不是还是不明白怎么算?没关系,举个例子:有前k大数 a,b。a与b挨着,那么分界线只能插在a上,1种,i+1-i=1,所以根据这个数目就是它们坐标之差。总之就是,记录前k大数的各个坐标之差,乘起来就好了。记得题意里说结果要mod 998244353
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<map> using namespace std; typedef long long ll; const int maxn=2e5+10; int main() { int n,k; cin>>n>>k; ll ans=1; int idx=-1; int x=0; ll sum=0; for(int i=1;i<=n;i++) { cin>>x; if(x>=n-k+1) { sum+=x; if(idx!=-1) { ans=(ans*(i-idx))%998244353; // cout<<i-idx<<endl; } idx=i; } } cout<<sum<<" "<<ans<<endl; }
原文:https://www.cnblogs.com/liyexin/p/12535868.html