树状数组(Binary Indexed Tree)

简介

树状数组是一种修改和查询的时间复杂度都为\(O(\log_2\!n)\)的一种数据结构。它支持查询区间和修改单点操作。
思想上，树状数组类似于线段树，还比线段树省空间，代码复杂度比线段树小，可以扩展到多维情况，不过适用范围比线段树小。
与线段树不同，树状数组在使用时无需建树，它的树状结构是数组模拟的。

结构分析

先看一张图：

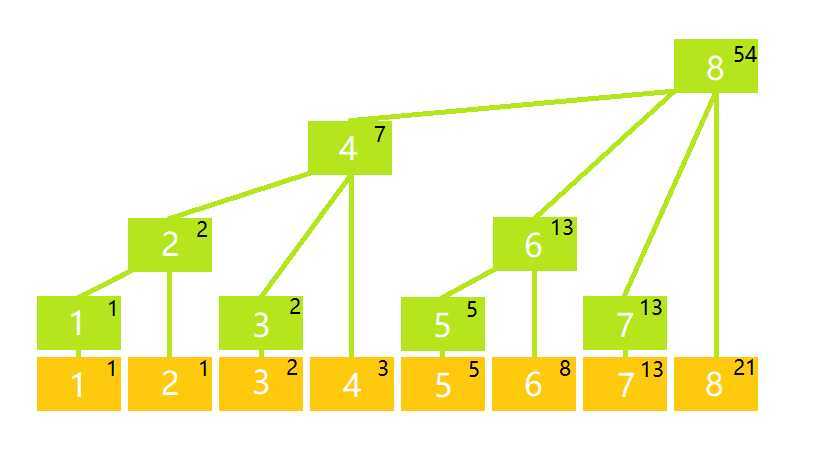
这张图展示了树状数组的结构（想象出来的结构）。其中橙色代表原数组节点\(A[i]\)，绿色代表树状数组节点\(C[i]\)，每个节点右上角的数代表该节点的权值。你可以发现，每个绿色节点权值都等于其子节点权值和。
其中有两个重要的规律：
\[C[i]=\sum_{j=i-\operatorname{lowbit}(i)+1}^{n}\!{A[j]}\qquad(1)\]
\[\sum_{j=1}^{i}\!A[j]=C[i]+C[i-\operatorname{lowbit}(i)]+C[i-\operatorname{lowbit}(i)-\operatorname{lowbit}(i-\operatorname{lowbit}(i))]\cdots\qquad(2)\]
其中\(i\)为正整数。
在解释这两个规律之前，先来看看\(\operatorname{lowbit}(i)\)是啥。

lowbit函数

这是一种位运算黑科技，函数原型是\(x\)&\(-x\)。它返回第一个小于等于\(x\)的\(2^k(k为非负整数)\)的数。
举个例子，\(x=4\)，\(\operatorname{lowbit}(x)=4\)；\(x=7\)，\(\operatorname{lowbit}(x)=1\)。
如果没看懂还是百度一下吧

解释

对\((1)\)式的解释：

对于\(C[i]\)，它对应\(A[i-\operatorname{lowbit}(i)+1]+\cdots+A[i]\)。
因此对\(A[i]\)加上\(k\)时，需要将每一个包含\(A[i]\)的\(C[j]\)加上\(k\)。
可以证明只有\(C[i]\)、\(C[i+\operatorname{lowbit}(i)]\)、\(C[i+\operatorname{lowbit}(i)+\operatorname{lowbit}(i+\operatorname{lowbit}(i))]\cdots\)包含\(A[i]\)。
举例：\(i=(6)_{10}=(110)_2\)，包含\(A[i]\)的\(C[]\)有\(C[6]\)、\(C[8]\)、\(C[16]\)等。

对\((2)\)式的解释：

计算\(A[1]+\cdots+A[i]\)时，把\(i\)减去\(\operatorname{lowbit}(i)\)，得到新的\(i_2\)，再将\(i_2\)减去\(\operatorname{lowbit}(i_2)\)，以此类推，直到\(i-\operatorname{lowbit}(i)\)为\(0\)为止。
举例：\(i=(6)_{10}=(110)_2\)，\(A[1]+\cdots+A[6]=C[(110)_2]+C[(100)_2]=C[6]+C[4]=13+7=20\)。
下面看看树状数组的基本操作“单点修改”和“区间查询”是如何实现的。

操作

单点修改

在原数组中\(A[i]\)的位置加上一个值，并维护树状数组。
根据上文对\((1)\)式的解释，可得如下代码：

inline void add(int x,int k)//维护树状数组C，对应于原数组A的操作就是A[i]+=k
{
    for(;x<=n;x+=x&-x)//x & -x 就是lowbit()函数
        c[x]+=k;
}

区间查询

计算\(A[1]+\cdots+A[i]\)。
根据上文对\((2)\)式的解释，可得如下代码：

inline int ask(int x)//查询A[1]+···+A[x]的值
{
    int ans=0;
    for(;x;x-=x&-x)
        ans+=c[x];
    return ans;
}

如果上文的解释你没看懂，可以体会一下这两段代码。

变式

区间修改，单点查询

这里利用了差分的思想（似乎是差分最广泛的应用）
我们发现，当\(A[l]~A[j]\)都加上一个值时，相邻的A[i]之差不变。
这启发我们利用差分进行变式，使其支持单点查询和区间修改操作。
可以用树状数组维护原数组的差分数组。
举例：A[]={1,2,3,5}，B[]={1,1,1,2}，C[]={1,2,1,5}。

模板

LG3304【模板】树状数组 1

模板题，上代码

#include<iostream>
using namespace std;
int n,m,a[1000005],tr[1000005];
inline void add(int x,int y)
{
    for(;x<=n;x+=x&-x)
        tr[x]+=y;
}
inline int ask(int x)
{
    int ans=0;
    for(;x;x-=x&-x)
        ans+=tr[x];
    return ans;
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=1,w;i<=n;i++)
    {
        scanf("%d",&a[i]);add(i,a[i]);
    }
    for(int i=1,t,x,y;i<=m;i++)
    {
        scanf("%d%d%d",&t,&x,&y);
        if(t==1)    add(x,y);
        else    printf("%d",ask(y)-ask(x-1));
    }
    return 0;
}

LG3368【模板】树状数组 2

又是模板题，上代码

//在实际操作时其实用原数组计算出的差分就行了
#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
long long a[500005],tr[500005],n,m;
inline void add(long long x,long long k)
{
    for(;x<=n;x+=x&-x)
        tr[x]+=k;
}
inline long long ask(long long x)
{
    int ans=0;
    for(;x;x-=x&-x)
        ans+=tr[x];
    return ans;
}
int main()
{
    long long t,x,y,k;
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%lld",&a[i]);
        add(i,a[i]-a[i-1]);//a[i]-a[i-1]是差分的定义
    }
    while(m--)
    {
        cin>>t;
        if(t==1)
        {
            scanf("%lld%lld%lld",&x,&y,&k);
            add(x,k),add(y+1,-k);//差分的原理1:区间[l,r]的元素加k，在原数组要依次维护区间[l,r]中的
                                               每一个元素，在差分数组只要让b[l]+k，b[r]-k就可以了
        }
        else
        {
            scanf("%lld",&x);
            printf("%lld\n",ask(x));//差分的原理2:A[i]=B[1]+···+B[i]
        }
    }
    return 0;
}

结语

树状数组还是蛮神奇的，跟线段树比起来，算法常数小，代码长度短，还省空间
下期预告：

• 用树状数组实现\(O(log_2 n)\)的区间查询，区间修改
• 用树状数组解决RMQ问题
• 应用树状数组（康托展开，求逆序对，全排列数化技术等等）
  \[\xrightarrow{\qquad}To\;be\;continued\cdots\]

树状数组(上)

原文：https://www.cnblogs.com/LZShuing-xuan/p/12502897.html