蒙特卡洛方法又称统计模拟法，随机抽样技术，是一种随机模拟方法，以概率和统计理论方法为基础的一种计算方法。是使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。为象征性地表明这一方法的概率统计特征，故借用赌城蒙特卡罗命名，这也是蒙特卡洛法的基本思想。当样本数量足够大时，我们可以用频率去估计概率。这也是求圆周率π的常用方法。当我们在（0，1）的范围内随机选择一个坐标（x, y）时，每个坐标点被选中的概率相等。则坐标落在边为1的正方形中的四分之一圆面的概率为：
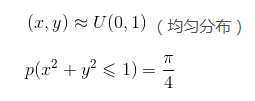通俗点说就是随机点落在四分之一圆面（第一象限）上的点的概率 与 随机点落在四分之一正方形（第一象限）的比为 四分之一圆面的面积 与 四分之一正方形的面积之比 。
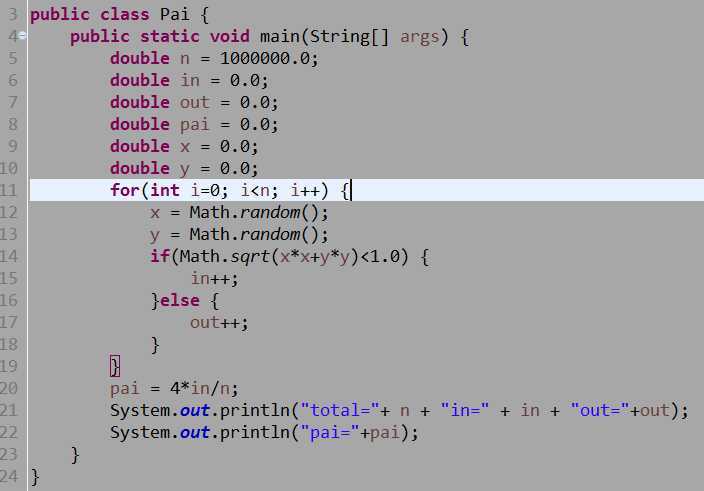
程序实现：
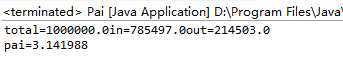
用1000000的随机样本数，样本数越大，圆周率越精确。跑了一下十亿的样本数，电脑要跑几十秒，跑出来的结果是3.14159522...
运行结果：
原文：https://www.cnblogs.com/jjunior/p/12535490.html