好难的数据结构啊。
今天刚学的树状数组,于是决定水一发算法笔记。
话不所说,让我们开始走进树状数组的世界吧。
先推荐 一篇文章,绝对可以好好看看。
众所周知,树状数组是一种修改和查询的时间复杂度都为 \(O(log_2n)\) 的一种数据结构。
它的本质是一个数组(而非一棵树),所以无需建树。
而它的基本用途是维护一个序列的前缀和(不知道的自行百度),从而进行区间查询。
那么它和线段树的区别是什么呢,请看下列解释:
A:同学,你知道线段树和树状数组的区别吗?
B:这么跟你说吧,树状数组有的功能线段树都有,所以线段树的应用范围广泛很多。
A:那有树状数组干什么。
B:别急,树状数组还是有好处的,比线段树省空间,代码复杂度比线段树小,可以扩展到多维情况。
A:但是我还是可以用线段树解决一切呀。
B:空间小的情况下只能用树状数组,而且还有更重要的一点。
A:???
B:高精知道吧,你完全可以用高精加去解决 \(1+1\) 等于几的问题,但是所有人都会直接加。
A:这和我的问题有什么关系?
B:树状数组就是简单的加法,而线段树就相当于高精。(高精时间长,空间大,码量大)
A:哦~,所以树状数组只是基础知识,只是为线段树做铺垫的。
B:也不能这么说,在能用树状数组的时候就尽量用它,其他的还是根据具体情况而定。
好的,既然你已经懂了,那就让我们正式进入树状数组的学习吧。??
先看一张图:(这图来自哪里你懂的)
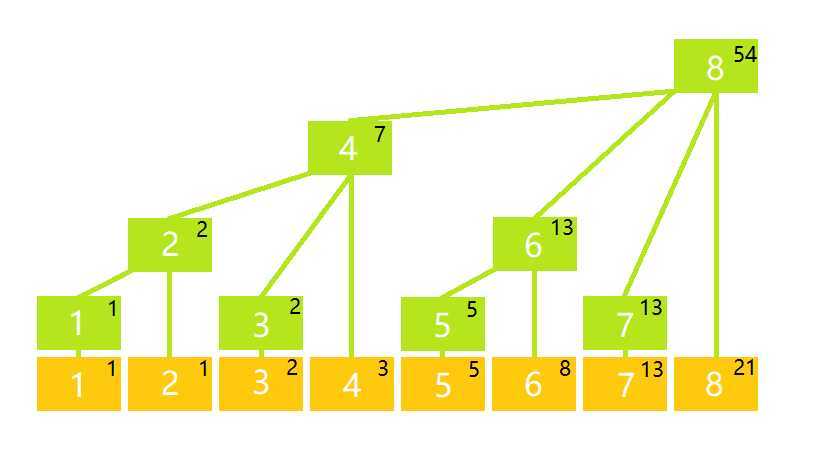
对于序列 \(a[]\) (即黄色的部分),我们建立一个数组 \(c[]\) 用来保存区间 \([x-lowbit(x)+1,x]\) 中所有数的和。
那么显然:
\[c[x]=\sum_{i=x-lowbit(x)+1}^{x} a[i]\]
过于简单,不进行讲述。
然后我们就有了一下两个操作。
void add(int x,int k){
while(x<=n){
tree[x]+=k;
x+=lowbit(x);
}
}int ask(int x){
int ans=0;
while(x>=1){
ans+=tree[x];
x-=lowbit(x);
}
return ans;
}#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<iostream>
#define N 2000010
using namespace std;
int n,m,tree[N];
int lowbit(int x){
return x & (-x);
}
void add(int x,int k){
while(x<=n){
tree[x]+=k;
x+=lowbit(x);
}
}
int ask(int x){
int ans=0;
while(x>=1){
ans+=tree[x];
x-=lowbit(x);
}
return ans;
}
int main(){
scanf("%d %d",&n,&m);
int a;
for(int i=1;i<=n;i++){
scanf("%d",&a);
add(i,a);
}
int flag,x,y;
for(int i=1;i<=m;i++){
scanf("%d %d %d",&flag,&x,&y);
if(flag==1){
add(x,y);
}
else{
int l=ask(x-1);
int r=ask(y);
printf("%d\n",r-l);
}
}
return 0;
}来介绍一下差分。
设数组 \(a[]={1,6,8,5,10}\),那么差分数组 \(b[]={1,5,2,-3,5}\)。
也就是说 \(b[i]=a[i]-a[i-1] (a[0]=0)\),那么 \(a[i]=b[1]+....+b[i]\) (这个很好证的)。
假如区间 \([2,4]\) 都加上 \(2\)的话,\(a\) 数组变为 \(a[]={1,8,10,7,10}\),\(b\) 数组变为 \(b={1,7,2,-3,3}\)。
发现,\(b\) 数组只有 \(b[2]\) 和 \(b[5]\) 变了,因为区间 \([2,4]\) 是同时加上 \(2\) 的,所以在区间内 \(b[i]-b[i-1]\) 是不变的。
所以对区间 \([x,y]\) 进行修改,只用修改 \(b[x]\)与 \(b[y+1]\)。
\(b[x]=b[x]+k\),\(b[y+1]=b[y+1]-k\)。
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<iostream>
#define N 2000010
using namespace std;
int n,m,tree[N],a[N];
int lowbit(int x){
return x & (-x);
}
void add(int x,int k){
while(x<=n){
tree[x]+=k;
x+=lowbit(x);
}
}
int ask(int x){
int ans=0;
while(x>=1){
ans+=tree[x];
x-=lowbit(x);
}
return ans;
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
}
int flag,x,y,k;
for(int i=1;i<=m;i++){
scanf("%d",&flag);
if(flag==1){
scanf("%d %d %d",&x,&y,&k);
add(x,k);
add(y+1,-k);
}
else{
scanf("%d",&x);
printf("%d\n",ask(x)+a[x]);
}
}
return 0;
}和归并排序求逆序对类似,树状数组同样是在 \(O(n\ log\ n)\) 的时间里求逆序对的。
逆序对就是序列中 \(a[i]>a[j]\) 且 \(i<j\) 的情况下的有序对。
我们可以先按照权值从大到小排序,现在要求的就是对于一个点有多少在他前面的点下标小于这个点。
然后用树状数组维护。从头到尾扫一遍,对于每个点,答案就是在这个点下标之前的下标有几个已经被访问过。
在将这个点在树状数组中+1,表示为被访问过。
但是要注意判重复的元素,同时排序时以序号大小作为第二关键字。(想一想为什么)
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<iostream>
#define N 500010
using namespace std;
int n,tree[N<<2];
long long ans=0;
struct node{
int x,id;
}a[N];
int read(){
int x=0,f=1;
char c=getchar();
while(c<'0' || c>'9') f=(f=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return f*x;
}
int lowbit(int x){
return x & -x;
}
bool cmp(node a,node b){
if(a.x==b.x) return a.id>b.id;
return a.x>b.x;
}
void add(int x,int k){
while(x<=n){
tree[x]+=k;
x+=lowbit(x);
}
return;
}
int ask(int x){
int ans=0;
while(x>0){
ans+=tree[x];
x-=lowbit(x);
}
return ans;
}
int main(){
n=read();
for(int i=1;i<=n;i++)
a[i].id=i,a[i].x=read();
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++)
ans+=ask(a[i].id),add(a[i].id,1);
printf("%lld\n",ans);
return 0;
}A Simple Problem with Integers
其实这个一般用线段树实现,但是也不是没有可能用树状数组实现的啦。(〃‘▽‘〃)
我们已经讨论过区间修改,单点查询问题和,我们知道可以用差分解决。
假设查分数组为 \(b[]\),那么 \(a\) 的前缀和 \(a[1\)~\(x]\) 的整体增加值就是:
\[\sum _{i=1}^x \sum_{j=1}^i b[j]\]
经过一系列的 玄学 数学推导,上式等于:
\[(x+1 \sum_{i=1}^x b[i]-\sum _{i=1}^x i\times b[i])\]
所以增加一个树状数组来记录 \(i\times b[i]\) 的前缀和即可(假设用 \(tree[i][1]\) 表示)。
那么,核心的加点操作就是:
add(0,x,k);
add(0,y+1,-k);
add(1,x,x*k);
add(1,y+1,-(y+1)*k);答案就是:
sum[y]+(y+1)*ask(0,y)-ask(1,y)-(sum[x-1]+x*ask(0,x-1)-ask(1,x-1))
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#define N 100010
using namespace std;
int n,m,a[N];
long long tree[2][N],sum[N];
int read(){
int x=0,f=1;
char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return f*x;
}
int lowbit(int x){
return x & -x;
}
long long ask(int type,int x){
long long ans=0;
while(x>0){
ans+=tree[type][x];
x-=lowbit(x);
}
return ans;
}
void add(int type,int x,int k){
while(x<=n){
tree[type][x]+=k;
x+=lowbit(x);
}
return;
}
int main(){
n=read();m=read();
for(int i=1;i<=n;i++){
a[i]=read();
sum[i]=sum[i-1]+a[i];
}
char c[2];
int x,y,k;
for(int i=1;i<=m;i++){
scanf("%s",c);
if(c[0]=='C'){
x=read();y=read();k=read();
add(0,x,k);
add(0,y+1,-k);
add(1,x,x*k);
add(1,y+1,-(y+1)*k);
}
else{
x=read();y=read();
long long ans=sum[y]+(y+1)*ask(0,y)-ask(1,y);
ans-=sum[x-1]+x*ask(0,x-1)-ask(1,x-1);
printf("%lld\n",ans);
}
}
return 0;
}其实也没有那么难的啦。
显然一个 ?? 的编号 = 它前面比它高的 ?? 数(即 \(a[i]\))+ 它后面比它高的 ?? 数 + 1
我们建立一个长度为 \(n\) 的 \(01\) 串 \(b\),那么起初全部为 \(0\)。然后 \(n\)~\(1\) 倒序处理每一个 \(a[i]\):
也就是说我们要实时维护一个 01 序列,支持查询并修改第 \(k\) 个 0 的位置。
显然用 树状数组 + 二分即可。
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
#define N 100010
using namespace std;
int n,ans[N],a[N],tree[N];
int read(){
int x=0,f=1;
char c=getchar();
while(c<'0' || c>'9') f=(c=='-')?-1:1,c=getchar();
while(c>='0' && c<='9') x=x*10+c-48,c=getchar();
return x*f;
}
int lowbit(int x){
return x&-x;
}
int ask(int x){
int ans=0;
while(x>0){
ans+=tree[x];
x-=lowbit(x);
}
return ans;
}
void add(int x,int k){
while(x<=n){
tree[x]+=k;
x+=lowbit(x);
}
return;
}
int main(){
n=read();
a[1]=0;
for(int i=2;i<=n;i++) a[i]=read();
for(int i=n;i>=1;i--){
int l=1,r=n,mid;
while(l<r){
mid=(l+r)>>1;
if(mid-ask(mid)>a[i]) r=mid;
else l=mid+1;
}
ans[i]=l;
add(l,1);
}
for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
return 0;
}树状数组的用途还有许多,以后会继续 \(Update\)。(咕咕咕)
特别鸣谢:LZshuing 的优秀文章。
完结撒花。
原文:https://www.cnblogs.com/lpf-666/p/12543665.html