(一)晶体的宏观性质
1.自限性:自发的形成封闭凹多面体;
2.解离性:眼某些确定方向的镜面(解离面)易劈裂;
3.晶面角守恒:同一品种晶体两个对应晶面间夹角恒定不变;
4.各向异性:不同方向上,物理性质不同;
5.均匀性:(同一方向上)任意两点物理性质相同;
6.对称性:在特定的某几个方向上,异向同性,且这种性质在不同方向上有规律的重复;
7.固定的熔点:加热晶体,晶体在特定温度融化且融化过程中温度不变;
(二)晶体的微观结构——晶格
1.基元与格点
??晶格中有许多周期性排列的点,称为格点,每一个格点代表一个基元。
(1)基元是晶体结构中最小的重复单元,可以包含1个或数个原子;
(2)格点既可以是基元重心的位置,也可以代表基元中的任意位置。
2.原胞与基矢
??原胞主要有两种:
(1)固体物理学原胞(简称原胞)
??取格点最近邻的三个格点做不共面矢量a1、a2、a3,并由此所得的平行六面体称为固体物理学原胞。固体物理学原胞的体积为:
\[V=(\vec{a}_1 × \vec{a}_2)· \vec{a}_3=\Omega
\]
??原胞的格点只在顶角上,面和内部均无格点,平均每个原胞含一个格点。
(2)结晶学原胞(简称晶胞)【布拉维原胞】
??基矢a、b、c的方向尽可能沿空间对称轴方向(一般是直角坐标轴)。结晶学原胞的体积为:
\[V=(\vec{a}×\vec{b})·\vec{c}=n\Omega \space\space\space\space n\in Z^{+}
\]
晶胞的格点既可以在顶角,又可以在面和内部。
??另外,还有一种维格纳-赛茨原胞,相当于正格子的第一布里渊区取法,这里不详述。
3.晶向、晶面及其指数
(1)晶向与晶向指数
??过任意两个格点连一直线(晶列),其取向称为晶向。
①平行晶列构成晶列族,晶列族包含所有格点;
②晶列上格点排列是周期性的;
③同族晶列上格点排列相同;
④同一平面内,相邻晶列间距离相同。
??晶向可以写作:
\[\vec{R}=\begin{cases} l_1\vec{a}_1+l_2\vec{a}_2+l_3\vec{a}_3&\text{[原胞]} \space\space\space\space l_i\in Z且互质\m\vec{a}+n\vec{b}+p\vec{c}&\text{[晶胞]}\space\space\space\space m,n,p\in Z且互质\end{cases}
\]
??对应的晶向指数为:
\[[l_1 l_2 l_3]\space\space or \space\space[mnp] \\\space
\when\space\space l_i \space (or\space others)\space<0 \space \space\space \space write \space as\space \bar{l}_i
\]
??由于空间对称性,存在等效晶向,其符号为<l1l2l3>。
(2)晶面、晶面指数(密勒指数)与晶面方程
??通过三个不共线格点所做平面,称为晶面。
①平行晶面构成晶面族,晶面族包含所有格点;
②晶面上格点排列是周期性的;
③同族晶面上格点排列相同;
④同族相邻晶列间距离相同。
??如果晶面的法向量为:
\[\vec{n}_0=\begin{cases} l_1\vec{a}_1+l_2\vec{a}_2+l_3\vec{a}_3&\text{[原胞]} \space\space\space\space l_i\in Z且互质\m\vec{a}+n\vec{b}+p\vec{c}&\text{[晶胞]}\space\space\space\space m,n,p\in Z且互质\end{cases}
\]
??则晶面指数为:
\[(l_1 l_2 l_3)\space\space or \space\space(mnp) \\\space
\when\space\space l_i \space (or\space others)\space<0 \space \space\space \space write \space as\space \bar{l}_i
\]
??对于等效的晶面使用{ }。
??晶面还可以由另一种方法确定:
阿羽依有理数定理(以原胞为例)
设晶面与基矢坐标轴交于:
\[(r\vec{a}_1,0,0)\space\space(0,s\vec{a}_2,0)\space\space(0,0,t\vec{a}_3)
\]
那么有必有:
\[l_1:l_2:l_3 =\frac{1}{r}:\frac{1}{s}:\frac{1}{t}\space\space\space\space r,s,t\in Q
\]
??设晶面法向量经过原点O和晶面上的点N,由于镜面的性质①和④,必有:
\[\overrightarrow{ON}=\mu d \space\space \mu\in Z
\]
??那么取镜面取任意一点A,做过原点的矢量,并与单位法向量点乘,有:
\[\overrightarrow{OA}·\vec{n}_0=\overrightarrow{OA}·\frac{\overrightarrow{ON}}{|\overrightarrow{ON}|}=|{\overrightarrow{ON}}|=\mu d \space\space \mu\in Z
\]
??这就是晶面方程。
4.晶格与晶系
(1)简单晶格
??晶体由一种周围环境完全相同的原子构成。一个原子对应一个格点,格点组成的网格为简单晶格。例如,简立方Cu:
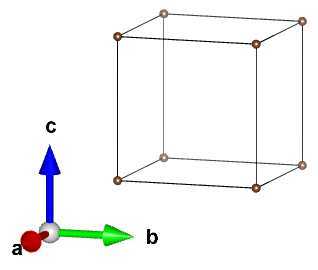
(2)复式晶格
??晶体包含两种或以上(周围环境不同的同种原子视为不同种)原子,各种原子均与格点呈相同排列方式(即一个格点包含多种原子),平移嵌套后形成晶格。例如,金刚石,为两组相差(a+b+c)/4的面心立方碳原子嵌套而成:
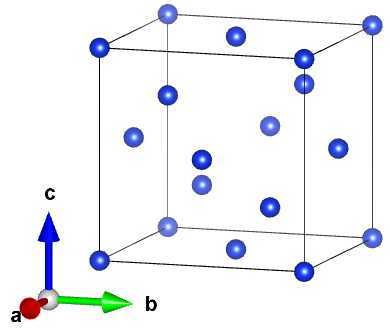
(3)晶格的密堆、配位、致密度
①密堆类型:
六角密堆 单层密堆积,以AB相间堆叠
立方密堆 单层密堆积,ABC方式堆叠(A、C层翻转180°)
②配位:一个原子周围最近邻原子的数量(依赖于原子半径比)
| 结构类型 |
配位 |
半径比r/R[r<R] |
| 密堆积 |
12 |
1 |
| 氯化铯型 |
8 |
0.732 - 1 |
| 氯化钠型 |
6 |
0.41 - 0.732 |
| 金刚石型 |
4 |
0.155 - 0.41 |
| 石墨层状 |
3 |
<0.155 |
| 链状 |
2 |
|
③致密度:以等体积的、半径尽量大的硬球替换格点,一个晶格中被硬球占据的体积与晶格体积之比即为致密度。
(4)七大晶系与十四种布拉维格子(格点的总体)
| 晶系 |
特征 |
布拉维格子 |
致密度 |
| 三斜 |
a1≠a2≠a3
α≠β≠γ |
简单三斜 |
/ |
| 单斜 |
a1≠a2≠a3
α=β=90° γ≠90° |
简单单斜
底心单斜 |
/ |
| 正交 |
a1≠a2≠a3
α=β=γ=90° |
简单正交
体心正交
底心正交
面心正交 |
/ |
三角
/菱方 |
a1=a2=a3
α=β=γ<120°
≠90° |
简单三角 |
/ |
| 四方 |
a1=a2≠a3
α=β=γ=90° |
简单四方
体心四方 |
/ |
| 六角 |
a1=a2≠a3
a3⊥a1,a2
<a1,a2>=120° |
六角 |
√2π/6 |
| 立方 |
a1=a2=a3
α=β=γ=90° |
简单立方
体心立方
面心立方 |
π/6
√3π/8
√2/6 |
、
(三)动量空间(倒格矢构成的倒空间)
1.倒格基矢与倒格矢
??倒格基矢可以由原胞基矢变换得到:
\[\vec{b}_i=2\pi \frac{\vec{a}_j \vec{a}_k}{[\vec{a}_j \times \vec{a}_k] \cdot \vec{a}_i}=2\pi \frac{\vec{a}_j \vec{a}_k}{\Omega}
\]
??那么倒格矢可以写为:
\[\vec{K}_h=h_1\vec{b}_1+h_2\vec{b}_2+h_3\vec{b}_3\space\space\space\space h_i\in Z
\]
??它们具有如下性质:
(1)当原胞基矢互相垂直时,|bi|=2π/|ai|;
(2)倒格子体积 Ω*=8π3/Ω
(3)正交性
\[\vec{a}_i \cdot \vec{b}_j=2\pi \delta_{ij}
\]
(4)与晶向的乘积为2π的整数倍
\[\vec{R}_l\times \vec{K}_h=(l_1\vec{a}_1+l_2\vec{a}_2+l_3\vec{a}_3)(h_1\vec{b}_1+h_2\vec{b}_2+h_3\vec{b}_3)\\\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space=(l_1h_1+l_2h_2+l_3h_3)2\pi=2\mu\pi \space \space\space\space \mu\in Z
\]
(5)倒格矢垂直于晶面族(h1 h2 h3)[利用阿羽依有理数定理易证]
2.倒格矢与x-p傅里叶变换对
??由晶格对称性和周期性知晶格的某个物理量V可以写成如下形式:
\[取 \space\space\space\space\vec{x}=\xi_1\vec{a}_1+\xi_2\vec{a}_2+\xi_3\vec{a}_3\space\space\space\space \xi_i\in (0,1)\\vec{R}_l=l_1\vec{a}_1+l_2\vec{a}_2+l_3\vec{a}_3\space\space\space\space l_i\in Z
\\ \space
\\implies V(\vec{x})=V(\vec{x}+\vec{R}_l)\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space
\\ \space
\\implies V(\vec{x})=\displaystyle\sum_{h_! h_2 h_3} {C_{h_1 h_2 h_3} e^{i2\pi(h_1\xi_1+h_2\xi_2+h_3\xi_3)}}
\\ \space
\\implies C_{h_1 h_2 h_3}=\int e^{-i2\pi(h_1\xi_1+h_2\xi_2+h_3\xi_3)}V(\vec{x}) d\tau
\\ \space
\\overset{2\pi\xi_i=\vec{b}_i\cdot\vec{x}}{\implies} 傅里叶变换对\begin{cases} V(\vec{x})=\displaystyle\sum_{h_! h_2 h_3} {C_{h_1 h_2 h_3} e^{i\vec{K}_h\cdot\vec{x}}} &\text{} \\C_{h_1 h_2 h_3}=\int e^{-i\vec{K}_h\cdot\vec{x}}V(\vec{x}) d\tau &\text{} \end{cases}
\]
??其中指数函数的形式相当于:
\[\vec{p}=\hbar\vec{K}_h
\\ \space
\e^{-i\vec{K}_h\cdot\vec{x}}=e^{\frac{i}{\hbar}\vec{p}\cdot\vec{x}}
\]
??也即晶体场周期物理量可以按自由粒子平面波函数展开,并由其复共轭求展开系数。
??容易验证:
\[V(\vec{x}+\vec{R}_l)=\displaystyle\sum_{h_1 h_2 h_3} {C_{h_1 h_2 h_3} e^{i\vec{K}_h\cdot(\vec{x}+\vec{R}_l)}}\\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space
=\displaystyle\sum_{h_1 h_2 h_3} {C_{h_1 h_2 h_3} e^{i\vec{K}_h\cdot\vec{x}}e^{i\vec{K}_h\cdot\vec{R}_l}}\\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space
=\displaystyle\sum_{h_1 h_2 h_3} {C_{h_1 h_2 h_3} e^{i\vec{K}_h\cdot\vec{x}}e^{i2\mu\pi}}\\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space
=\displaystyle\sum_{h_1 h_2 h_3} {C_{h_1 h_2 h_3} e^{i\vec{K}_h\cdot\vec{x}}}=V(\vec{x})
\]

