https://zhuanlan.zhihu.com/p/44216830

一、处理回归问题：

mean_squared_error（MSE）

mean_absolute_error (MAE)

二、处理分类问题

先 sigmoid 再求交叉熵

先 softmax 再求交叉熵

weighted_cross_entropy_with_logits：带权重的 sigmoid 交叉熵

hinge_loss：铰链损失函数 —— SVM 中使用

三、siamese network

Contrastive Loss，这种损失函数可以有效的处理孪生神经网络中的paired data的关系

整理：

优点、缺点、tf公式、公式、

mean_squared_error：均方根误差（MSE）

优点是便于梯度下降，误差大时下降快，误差小时下降慢，有利于函数收敛。

缺点是受明显偏离正常范围的离群样本的影响较大

Sigmoid 函数的输出表征了当前样本标签为 1 的概率：

很明显，当前样本标签为 0 的概率就可以表达成：

把上面两种情况整合到一起：

我们希望 log P(y|x) 越大越好，反过来，只要 -log P(y|x) 越小就行了。令 Loss = -log P(y|x)即可。则得：

已经推导出了单个样本的损失函数，是如果是计算 N 个样本的总的损失函数，只要将 N 个 Loss 叠加起来就可以了：

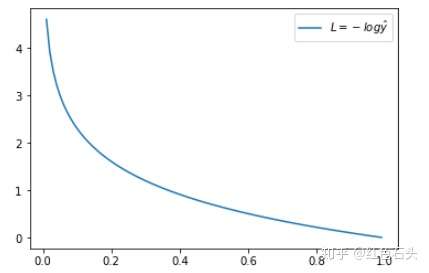
当 y = 1 时：

预测输出越接近真实样本标签 1，损失函数 L 越小；预测输出越接近 0，L 越大。

当 y = 0 时：

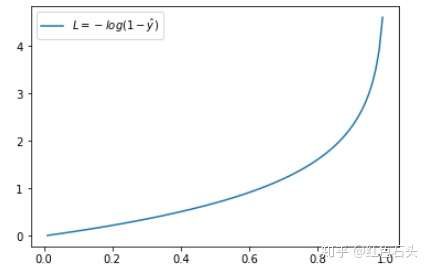
预测输出越接近真实样本标签 0，损失函数 L 越小；预测函数越接近 1，L 越大。

Sigmoid vs Softmax 输出层选择

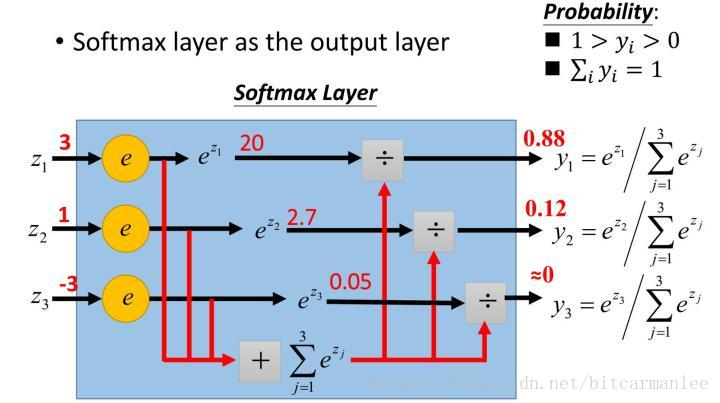
为什么现在一般深度学习的分类模型最后输出层都用Softmax而不是简单的Sigmoid？

当Sigmoid函数的某个输出接近1或者0的时候，就会产生梯度消失，严重影响优化速度，而Softmax没有这个问题。

【深度学习】损失函数

原文：https://www.cnblogs.com/pocahontas/p/12545334.html