Softmax的含义:Softmax简单的说就是把一个N*1的向量归一化为(0,1)之间的值,由于其中采用指数运算,使得向量中数值较大的量特征更加明显。
如图所示,在等号左边部分就是全连接层做的事。
现在你知道softmax的输出向量是什么意思了,就是概率,该样本属于各个类的概率!
那么softmax执行了什么操作可以得到0到1的概率呢?先来看看softmax的公式(以前自己看这些内容时候对公式也很反感,不过静下心来看就好了):
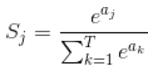
公式非常简单,前面说过softmax的输入是WX,假设模型的输入样本是I,讨论一个3分类问题(类别用1,2,3表示),样本I的真实类别是2,那么这个样本I经过网络所有层到达softmax层之前就得到了WX,也就是说WX是一个31的向量,那么上面公式中的aj就表示这个31的向量中的第j个值(最后会得到S1,S2,S3);而分母中的ak则表示31的向量中的3个值,所以会有个求和符号(这里求和是k从1到T,T和上面图中的T是对应相等的,也就是类别数的意思,j的范围也是1到T)。因为e^x恒大于0,所以分子永远是正数,分母又是多个正数的和,所以分母也肯定是正数,因此Sj是正数,而且范围是(0,1)。如果现在不是在训练模型,而是在测试模型,那么当一个样本经过softmax层并输出一个T*1的向量时,就会取这个向量中值最大的那个数的index作为这个样本的预测标签。
因此我们训练全连接层的W的目标就是使得其输出的WX在经过softmax层计算后其对应于真实标签的预测概率要最高。
举个例子:假设你的WX=[1,2,3],那么经过softmax层后就会得到[0.09,0.24,0.67],这三个数字表示这个样本属于第1,2,3类的概率分别是0.09,0.24,0.67。取概率最大的0.67,所以这里得到的预测值就是第三类。
弄懂了softmax,就要来说说softmax loss了。
那softmax loss是什么意思呢?如下:
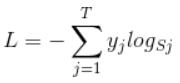
首先L是损失。Sj是softmax的输出向量S的第j个值,前面已经介绍过了,表示的是这个样本属于第j个类别的概率。yj前面有个求和符号,j的范围也是1到类别数T,因此y是一个1*T的向量,里面的T个值,而且只有1个值是1,其他T-1个值都是0。那么哪个位置的值是1呢?答案是真实标签对应的位置的那个值是1,其他都是0。所以这个公式其实有一个更简单的形式:
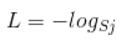
当然此时要限定j是指向当前样本的真实标签。
来举个例子吧。假设一个5分类问题,然后一个样本I的标签y=[0,0,0,1,0],也就是说样本I的真实标签是4,假设模型预测的结果概率(softmax的输出)p=[0.1,0.15,0.05,0.6,0.1],可以看出这个预测是对的,那么对应的损失L=-log(0.6),也就是当这个样本经过这样的网络参数产生这样的预测p时,它的损失是-log(0.6)。那么假设p=[0.15,0.2,0.4,0.1,0.15],这个预测结果就很离谱了,因为真实标签是4,而你觉得这个样本是4的概率只有0.1(远不如其他概率高,如果是在测试阶段,那么模型就会预测该样本属于类别3),对应损失L=-log(0.1)。那么假设p=[0.05,0.15,0.4,0.3,0.1],这个预测结果虽然也错了,但是没有前面那个那么离谱,对应的损失L=-log(0.3)。我们知道log函数在输入小于1的时候是个负数,而且log函数是递增函数,所以-log(0.6) < -log(0.3) < -log(0.1)。简单讲就是你预测错比预测对的损失要大,预测错得离谱比预测错得轻微的损失要大。
理清了softmax loss,就可以来看看cross entropy了。
corss entropy是交叉熵的意思,它的公式如下:
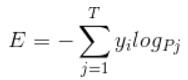
是不是觉得和softmax loss的公式很像。当cross entropy的输入P是softmax的输出时,cross entropy等于softmax loss。Pj是输入的概率向量P的第j个值,所以如果你的概率是通过softmax公式得到的,那么cross entropy就是softmax loss。
softmax 虽然简单,但是其实这里面有非常的多细节值得一说。
我们挨个捋一捋。
首先,softmax 的作用是把 一个序列,变成概率。
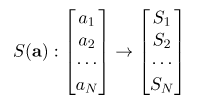
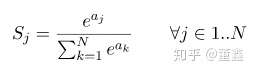
他能够保证:
从概率的角度解释 softmax 的话,就是
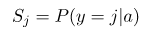
这里穿插一个“小坑”,很多deep learning frameworks的 文档 里面 (PyTorch,TensorFlow)是这样描述 softmax 的,
take logits and produce probabilities
很明显,这里面的 logits 就是 全连接层(经过或者不经过 activation都可以)的输出,probability就是 softmax 的输出结果。 这里 logits 有些地方还称之为 unscaled log probabilities。这个就很意思了,unscaled probability可以理解,那又为什么 全连接层直接出来结果会和 log 有关系呢?
原因有两个:
好的,我们把话题拉回到 softmax。
softmax,顾名思义就是 soft 版本的 max。我们来看一下为什么?
举个栗子,假如 softmax 的输入是:
softmax 的结果是:
我们稍微改变一下输入,把 3 改大一点,变成 5,输入是
softmax 的结果是:
可见 softmax 是一种非常明显的 “马太效应”:强(大)的更强(大),弱(小)的更弱(小)。假如你要选一个最大的数出来,这个其实就是叫 hardmax。那么 softmax 呢,其实真的就是 soft 版本的 max。
这种 soft 版本的 max 在很多地方有用的上。因为 hard 版本的 max 好是好,但是有很严重的梯度问题,求最大值这个函数本身的梯度是非常非常稀疏的(比如神经网络中的 max pooling),经过hardmax之后,只有被选中的那个变量上面才有梯度,其他都是没有梯度。这对于一些任务(比如文本生成等)来说几乎是不可接受的。所以要么用 hard max 的变种,比如 Gumbel,
Categorical Reparameterization with Gumbel-Softmax亦或是 ARSM
ARSM: Augment-REINFORCE-Swap-Merge Estimator for Gradient Backpropagation Through Categorical Variables,要么就直接 softmax。
softmax 的代码实现看似是比较简单的,直接套上面的公式就好
def softmax(x):
"""Compute the softmax of vector x."""
exps = np.exp(x)
return exps / np.sum(exps)但是这种方法非常的不稳定。因为这种方法要算指数,只要你的输入稍微大一点,比如:
分母上就是
很明显,在计算上一定会溢出。解决方法也比较简单,就是我们在分子分母上都乘上一个系数,减小数值大小,同时保证整体还是对的
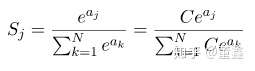
把常数 C 吸收进指数里面
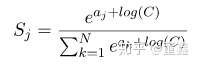
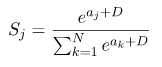
这里的D是可以随便选的,一般可以选成
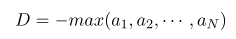
具体实现可以写成这样
def stablesoftmax(x):
"""Compute the softmax of vector x in a numerically stable way."""
shiftx = x - np.max(x)
exps = np.exp(shiftx)
return exps / np.sum(exps)这样一种实现数值稳定性已经好了很多,但是仍然会有数值稳定性的问题。比如输入的值差别过大的时候,比如
这种情况即使用了上面的方法,可能还是报 NaN 的错误。但是这个就是数学本身的问题了,大家使用的时候稍微注意下。
一种可能的替代的方案是使用 LogSoftmax (然后再求 exp),数值稳定性比 softmax 好一些。
可以看到,LogSoftmax省了一个指数计算,省了一个除法,数值上相对稳定一些。另外,其实 Softmax_Cross_Entropy 里面也是这么实现的
下面我们来看一下 softmax 的梯度问题。整个 softmax 里面的操作都是可微的,所以求梯度就非常简单了,就是基础的求导公式,这里就直接放结果了。
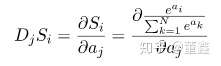
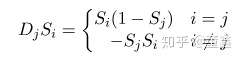
所以说,如果某个变量做完 softmax 之后很小,比如 ,那么他的梯度也是非常小的,几乎得不到任何梯度。有些时候,这会造成梯度非常的稀疏,优化不动。
先说结论,
softmax 和 cross-entropy 本来太大的关系,只是把两个放在一起实现的话,算起来更快,也更数值稳定。
cross-entropy 不是机器学习独有的概念,本质上是用来衡量两个概率分布的相似性的。简单理解(只是简单理解!)就是这样,
如果有两组变量:
如果你直接求 L2 距离,两个距离就很大了,但是你对这俩做 cross entropy,那么距离就是0。所以 cross-entropy 其实是更“灵活”一些。
那么我们知道了,cross entropy 是用来衡量两个概率分布之间的距离的,softmax能把一切转换成概率分布,那么自然二者经常在一起使用。但是你只需要简单推导一下,就会发现,softmax + cross entropy 就好像
“往东走五米,再往西走十米”,
我们为什么不直接
“往西走五米”呢?
cross entropy 的公式是
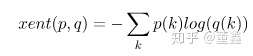
这里的 就是我们前面说的
LogSoftmax。这玩意算起来比 softmax 好算,数值稳定还好一点,为啥不直接算他呢?
所以说,这有了 PyTorch 里面的 torch.nn.CrossEntropyLoss (输入是我们前面讲的 logits,也就是 全连接直接出来的东西)。这个 CrossEntropyLoss 其实就是等于 torch.nn.LogSoftmax + torch.nn.NLLLoss。
原文:https://www.cnblogs.com/newton001/p/12548828.html